О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ.
(ГОНИОМЕТРИЯ.)
I. Тригонометрические функции острого угла.
§ 12. Зависимость между тригонометрическими функциями
одного и тогоже угла.
Между тригонометрическими функциями одного и того же угла легко обнаружить весьма простые зависимости (черт. 9).

1) Из прямоугольного треугольника ОВС имеем:
ВС2 + ОС2 = ОВ2.
Разделив здесь обе части на R2, получим:
(BC/R)2 + (OC/R)2 = (OB/R)2
или
sin2α+ cos2α = l. (I)
2) Из подобия треугольников ODA и ОВС имеем:
AD/OA= BC/OC ;
отсюда, заменяя ОА через R и разделив на R оба члена второго отношения, найдем:

или
tg α= sinα/cos α (II)
3) Из подобия треугольников ЕОМ и ОВС находим:
ME/OM= OC/BC ;
откуда

или
ctg α= cosα/sin α (III)
4) Из подобия треугольников ODA и ОBС находим:
OD/OA= OB/OC
отсюда

или
sec α= 1/cos α,
откуда
sec α • cos α= l. (IV)
5) Из подобия треугольников ЕОМ и ОВС имеем:
OE/OM= OB/OC
отсюда

или
cosec α = 1/sin α
откуда
cosec α • sin α = 1. (V)
§ 13. Между тригонометрическими функциями одного угла существует только пять различных соотношений. Чтобы убeдиться в этом, начнем с построения.
Дeйcтвительно, достаточно одной функции, чтобы построить угол (§ 10); а полученный угол определит собой остальные пять функций; таким образом, если известна одна функция, то по ней можно найти остальные пять. Но для определения пяти неизвестных мы должны иметь и пятъ уравнений, независимых друг от друга. Если бы таких уравнений было шесть, то для всех шести функций получились бы определенные значения, между тем как они изменяются вместе с углом.
§ 14. Кроме пяти основных формул, полученных в § 12, полезно запомнить еще следующие три, которые можно уже вывести из основных.
1) Перемножая соответственные части равенств (II) и (III), будем иметь:
tg α • ctg α = 1. (VI)
2) Деля равенство (I) на cos α и применяя формулы (II) и (IV), получим (если переставим слагаемые первой части):
l + tg2 α =sec2 α. (VII)
3) Деля равенство (I) на sin2α и применяя формулы (III) и (V), найдем:
l + ctg2 α = cosec2 α. (VIII)
Замечание 1. Самостоятельно формула (VI) получается из подобия треугольников, а формулы (VII) и (VIII) — при помощи теоремы Пифагора.
Замечание 2. Заметим для памяти, что в обычном ряде функции sin, cos, tg, ctg, sec, cosec, равно удаленные от концов, дают в произведении единицу [см. формулы (IV), (V) и (VI)].
Основными функциями мы будет считать sin, cos и tg (из них простейшие — sin и cos), а остальные три суть количества, обратные им:
ctg α = 1/tg α, sec α = 1/cos α и cosec α = 1/sin α.
§ 15. С помощью формул, полученных в §§ 12 и 14, легко по одной функции найти все остальные. Так, например, если tg α = 3/4 , то будем иметь последовательно:
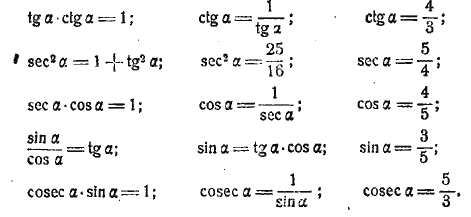
Еще пример. Выражая все функции через sin α , получим:

§ 16. Из подобия треугольников OBC, ODA и EOM (черт. 9) видно, между прочим, что шесть тригонометрических функций острого угла представляют собою не что иное, как шесть различных отношений, возможных между сторонами одного прямоугольного треугольника, взятыми попарно.

Действительно, из сторон треугольника ОВС можно составить следующие шесть отношений: BC/OB, OC/OB, BC/OC, OC/BC, OB/OC и OB/BC.
Но, описав дугу АВМ и построив треугольники ODA и ЕОМ, мы заменяем указанный ряд отношении следующим: BC/R, OC/R, AD/R, ME/R, OD/R и OE/R. Такая зaмена представляет значительные преимущества, одно из которых состоит, например, в том, что отношения принимают при этом вид дробей, приведенных к общему знаменателю, чем облегчается их сравнение между собой.