О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ.

(ГОНИОМЕТРИЯ.)

II. Тригонометрические функции углов от 90 до 360°.

§ 32. Вычисление угла по данному значению тригонометрической функции
(в пределах  от 0 до 360°).

Мы  уже видели в § 26, что при построении угла, соответствующего данному значению тригонометрической функции, получаются два угла, принадлежащие каким-нибудь двум четвертям. Величину этих углов можно определить по формулам приведения, пользуясь этими формулами в обратном смысле.

Поясним это на примерах:

1)  sin x = ¹/₂; найти угол х. Перзый   ответ:  х₁ =30°; второй угол, имеющий данный синус, это угол II четверти:

180° —30° =150°;

второй ответ: х₂ =150°.

2)   cos х = 0,974;   по   натуральным таблицам имеем: х₁ = 13°; кроме того, положительное  значение  косинуса   имeется   еще в IV четверти:

х₂ = 360°— 13° = 347°.

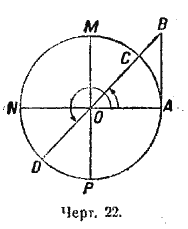
3)  tg x = l; соответствующий острый угол есть 45°; х₁ = 45°. По чертежу 22  видно,  что х₂ = 180° + 45° = 225°.

4)  sin.x = — ¹/₂ ; найти угол х. Отрицательные значения синуса имеются в III  и  IV четвертях; зная, что sin 30° = + ¹/₂,  заключаем, что искомый угол х₁ =180° + 30° = 210°;
х₂ =360° —30° = 330°