О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ.
(ГОНИОМЕТРИЯ.)
III. Углы отрицательные. Углы, большие 360°.
§ 45. Общий вид дуг, имеющих конец в данной точке окружности.
Пусть на чертеже 32 дуга АСВ содержит 64°. Очевидно, что все дуги, которые отличаются от 64° на полное число окружностей, оканчиваются также в точке В (предполагая общее начало в точке А).

Отсюда найдем, что дуги, имеющие конец в точке В, суть следующие: 64°, 424°, 784°, 1144° и т. д., а также: — 296°, — 656°,— 1016° и т. д. Все эти дуги можно выразить одной и той же формулой 64° + 360° • п, принимая за п различные целые числа как положительные, так и отрицательные, а также нуль.
Вообще, если α есть одна из дуг, имеющих данные начало и конец, то общий вид всех дуг, имеющих те же самые начало и конец, есть α + 360° • п (иначе α + 2πп).
Мы говорили о дугах, но полученные формулы можно отнести и к таким углам, у которых начальный и конечный радиусы одни и те же.
§ 46. Графики тригонометрических функций.
Изменения тригонометрических функций с изменением аргумента от 0 до 360° представлены в таблице § 29, но эта таблица содержит только ряд отдельных значений и потому не дает полного представления о ходе непрерывного изменения функций с изменением аргумента. Чтобы получить представление о непрерывном изменении функций, прибегают к графическому изображению их изменения.
С этой целью возьмем две взаимноперпендикулярные прямые линии ОХ и OY, называемые осями координат (черт. 33). Вдоль оси ОХ будем откладывать отрезки, изображающие в произвольном масштабе числовые значения аргумента, а вдоль оси OY— отрезки, изображающие в другом произвольном масштабе числовые значения функции.
При откладывании отрезков будем соблюдать правило знаков Декарта.

Положительные значения откладываются от начальной точки О вправо и вверх, отрицательные — влево и вниз (положительные направления осей на чертежах отмечены стрелками).
По оси ОХ отложим несколько равных отрезков, например 12;каждый из них будет изображать угол в 30° (или π/6) ; таким образом, все 12 отрезков, или расстояние ОА, изображают угол в 360°, или 2π (черт. 33). Чтобы на оси OY отложить числовые значения тригонометрической функции синуса, начертим вспомогательную окружность с центром О1, лежащим где-нибудь на оси ОХ. Радиус окружности O1M0 будет изображать собою числовое значение функции, равное единице. Начиная от точки М0, делим окружность на 12 равных частей (по числу делений на оси ОХ, соответствующих углу в 360°). Для найденных точек делений М0, M1,... , М11 строим линии синуса
М1Р1, М2Р2,... , М11Р11.
Так как радиус окружности равен единице, то длины построенных тригонометрических линий будут в принятом нами масштабе изображать числовые значения синуса. При помощи ряда прямых линий, параллельных оси ОХ, перенесем значения синуса на ось OY.
В каждой точке деления на оси ОХ восставим перпендикуляры к оси ОХ и на этих перпендикулярах отложим отрезки, выражающие соответствующие числовые значения синуса. Когда требуемые длины перпендикуляров будут построены, надо через полученные концы их провести кривую линию. Эта линия, проходящая через концы отрезков, изображающих на чертеже числовые значения синуса, будет изображать изменение функции синуса с изменением аргумента (дуги). Такая линия называется графиком функции.
На чертеже 33 представлен график синуса в пределах угла от 0 до 360°.
Чем больше точек деления мы возьмем, на чем большее число частей мы разделим отрезок ОА и вспомогательную окружность, тем больше точек графика мы получим и тем точнее его построим с помощью лекала.
Значения синуса можно находить не геометрическим построением, а взять из таблицы.
График синуса представляет собой кривую линию, называемую синусоидой.
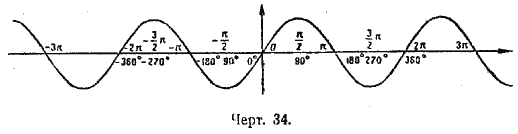
График синуса, построенный для положительных углов в пределах одной окружности, можно распространить на любые значения углов как положительных, так и отрицательных. По образцу графика синуса можно построить график косинуса, тангенса, котангенса. На чертежах 34, 35, 36 представлены синусоида, косинусоида и тангенсоида в пределах от —3π до + 3π.