О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ.
(ГОНИОМЕТРИЯ.)
III. Углы отрицательные. Углы, большие 360°.
§ 47. Общий вид углов, соответствующих данному значению
тригонометрической функции.
В § 26 было указано, что по данной тригонометрической функции получаются два положения подвижного радиуса; в § 32 мы выражали их положительными углами х1 и х2, меньшими 360°. Но с расширением границ аргумента от 0 до +∞ и от 0 до — ∞каждому радиусу, принятому за конечный, будет соответствовать уже не один угол, а бесконечный ряд углов, положительные и отрицательных; таким образом, теперь данному значению функции будут соответствовать углы, составляющие два бесконечных ряда. Все эти углы можно выразить, по § 45, с помощью х1 и х2, а именно: общий вид углов одного ряда с х1есть х1+360° • п, а общий вид углов другого ряда: х2+360° • п.
Мы получили общее решение вопроса в виде двух формул с двумя основными углами. Сейчас увидим, что они сводятся и к одному основному углу, но уже для различных функций различно.
Перейдем к отдельным функциям (для простоты возьмем примеры числовые и без применения таблиц).
1. a) sin х = 1/2 .
Искомый угол равен или 30° или 150°; следовательно, будем иметь:
х1 = 30°+ 360° • п и х2 = 150°+ 360° • п.
Эти выражения преобразуем так:
х1 =180°• 2п +30°;
х2= 180° —30°+180° • 2п = 180° (2п+1) —30°.
Здесь знак перед 30° зависит от четности (2п) или нечетности (2п + 1) множителя при 180°, а эту зависимость можно выразить с помощью степени отрицательной единицы; тогда вместо двух формул получим одну следующую:
х =180°• т+ 30°• (—1)m,
где т означает произвольное целое число, безразлично — четное или нечетное.
При т четном эта формула дает х1, а при т нечетном х2:
б) sin х = — 1/2; х1 = 210° +360° • п и х2 = 330° + 360° • п.
Можно уменьшить абсолютную величину основных углов, взяв для них отрицательные значения; тогда будем иметь:
х1 = —150° + 360° • kи х2 = — 30°+360° • k,
или в другом виде:
х1= — 150°+ 180° • 2k = — 150° + 180° —180° + 180° • 2k = 30° +180° (2k— 1)
и
х2 = 180°• 2k— 30°,
а эти две формулы можно соединить в одну следующую:
х =180°• т— 30°• (—1)m,
которая при т четном дает х1, а при т нечетном х2.
2. a) cos x= 1/2; х1 = 60°+ 360° • п и х2 = 300°+ 360° • п.
Если же воспользуекся в качестве основных также отрицательными углами, то получим:
х1 = 60°+ 360° • m и х2 = — 60° + 360°• m,
что можно написать слитно в виде:
х = 360° • m ± 60°.
б) cos x= — 1/2; х1 = 120° + 360° • п и х2= 240° + 360° • п.
Можно выразить х1и х2еще следующими формулами:
х1 = 120° + 360° • m и х2 = —120° +360° • m,
а их можно написать слитно в виде:
х = 360° • m ± 120°.
3. a) tg x =1; х1= 45°+ 360° • п и х2 = 225°+ 360° • п,
что можно представить в виде:
х1 = 45°+ 180°• 2п ;
х2= 45° + 180° • (2п+1) ;
а последние две формулы можно заменить одной следующей:
x = 45°+180° • т,
которая при т четном дает х1, а при т нечетном х2.
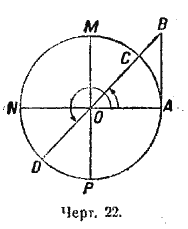
Формулу x = 45°+180° • т легко получить еще из следующего: чертеж 22, в котором точки С и D лежат на одном диаметре, показывает, что в ряде дуг всевозможной величины, от — ∞ до + ∞, дуги, имеющие один и тот же тангенс, встречаются через каждые 180°; таким образом искомые дуги составят арифметическую прогрессию с разностью 180°; общим членом этой прогрессии и будет
x = 45°+180° • т
б) tg x = — 1.
Рассуждая так же, как в п. а), получим:
х1= 135° + 360° • п и х2= 315°+360° • п,
или:
x = 135°+180° • т,
или еще:
x = — 45°+180° • k.
4. a) ctg x = √3
Вопрос решается совершенно так же, как в случае тангенса. Получим:
х1= 30° + 360° • п и х2= 210°+360° • п;
или:
x = 30°+180° • т.
б) ctg x= — √3 .
Рассуждая, как и в случае тангенса, найдем:
х1= 150° + 360° • п и х2= 330°+360° • п;
или:
x = 150°+180° • т,
а также x = — 30°+180° • k.
5 и 6. Если даны секанс и косеканс, то сначала переходим соответственно на косинус или синус.