О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ.

(ГОНИОМЕТРИЯ.)

III. Углы отрицательные. Углы, большие 360°.

§ 48. Обратные круговые функции.

Если мы имеем одно уравнение с двумя неизвестными, то из него можно определить любое неизвестное через другое. Например, если имеем; 2х + 3у = 6, то:

а) у = 2 — ²/₃ х;  б)   x = 3 — ³/₂ y.

Первое уравнение дает выражение у в функции х. Второе, наоборот, дает выражение х в функции у. В общем все три уравнения выражают одну и ту же зависимость между переменными x и у, но только форма выражения этой зависимости разная; первое уравнение не решено ни относительно х, ни относительно у, в следующем за функцию принято у, за аргумент х; в последнем за функцию принято х, за аргумент у.

Такие две функции, которые выражают одну и ту же зависимость между переменными х и у, но в одной за функцию принято у, а в другой за функцию принято х, называются взаимно-обратными. Любую из них можно принять за прямую; тогда другая будет обратная.

Примеры взаимнообратных функций:

у = 5х + 3;       х =  ^(у—3)/₅;

у = 2х;             х = ¹/₂ у

у = х²;             х = ±√ у ;

у = ³√х  ;         х = у³.

Понятие обратности можно применить и к тригонометрическим функциям.

Например, мы употребляем равенство: y = sin x; это значит, что  у есть синус дуги х; значит,   обратно, х есть  дуга, синус которой y. Точно  так  же: ¹/₂ = sin 30°, т. е. половина есть синус дуги в 30°. Наоборот, 30° есть дуга, синус которой равен половине.

Вместо того чтобы объяснять обратную зависимость словами, употребляют особый знак, обозначающий слово дуга: arc (читается „арк"; по-французски означает, дуга, арка).

Таким образом можно написать:

¹/₂ = sin 30°;       30° = arc sin ¹/₂;

¹/₂ = cos 60°;       60° = arc cos ¹/₂;

1= tg 45°;         45° = arc tg 1;

sin 16° = 0,276;         16° = arc sin 0,276;

cos ^π/₄ = 0,707;           ^π/₄  = arc cos 0,707;

1= sin90°;        90° = arc sin 1;

1= cos 0°;           0° = arc cos 1;

— 1 = cos π;      π = arc cos (—1);

tg ^π/₂ =  ∞ ;         ^π/₂ = arc tg ∞

sin ^π/₄ = cos ^π/₄ = ¹/₂√2;

^π/₄ = arc sin ¹/₂√2 = arc cos ¹/₂√2.

На чертеже 37 дуга обозначена через х, ее синус черзз т, ее тангенс через р. Значит, х есть дуга, синус которой т, а тангенс р; или:

х = arc sin т;   х = arc tg p.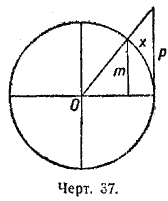             

Пользуясь   тригонометрическими   таблицами,   мы   решаем тоже две обратные задачи и пользуемся как прямыми, так и обратными тригонометрическими функциями.   Если дана дуга (или угол), то мы отыскиваем тригонометрическую функцию: наоборот,  если  дана тригонометрическая   функция  и   мы отыскиваем угол, то  мы  вычисляем   значение  обратной  тригонометрической функции.

Из § 47 мы знаем, что одной и той же тригонометрической функции соответствует бесчисленное множество дуг, имеющих одно и то же начало; например, синусу, равному половине, соответствуют дуги: 30°, 150°, 390°, 510°,...; основные из них, 30° и 150°, имеют синус, равный половине, но если прибавить к каждой по 360°, то и новые дуги будут иметь тот же синус. Следовательно, обратные тригонометрические функции есть функции  многозначные.

§ 49. В предыдущих примерах мы ограничивались наименьшей дугой, соответствующей данной тригонометрической функции, но можно было дать и общее выражение всех дуг, имеющих данный синус, косинус, тангенс. Если имеют в виду не наименьшее, а общее выражение всех дуг, имеющих данный синус, то обозначение дуги пишут с большой буквы;   например:

arc sin ¹/₂ = 30°;    но   Arc sin ¹/₂ = 180°• m + ( — l)^m30°,

или

arc tg 1 = 45°,   но  Arc tg 1= 45° + 180°• m.

Эти формулы взяты из § 47 (общий вид углов, соответствующих данному значению тригонометрической функции), но там еще не употреблялось обозначение обратной функции.

Если воспользоваться формулами § 47 и обобщить их, замени числовые значения буквенными, то получим следующую таблицу прямых и обратных тригонометрических функций:

y = sin x:;       Arc sin y = mπ  +  ( — l)^mx;

y = cos x;       Arc cos y = 2mπ ± x;

y = tg x;        Arc tg y = mπ   + x;

y= ctg x;        Arc ctg  y = mπ + x.

Большею частью, однако, по данной тригонометрической функции отыскивают наименьшую дугу (arc). При этом для положительных значений всех тригонометрических функций берут дугу в I четверти (от 0 до ^π/₂ ) ; для отрицательных значений синуса, тангенса, котангенса и косеканса берут дугу в I отрицательной четверти (от 0 до — ^π/₂) ; для отрицательного косинуса и секанса берут дугу во II четверти (от ^π/₂ до π).

Таким образом, для всех возможных  значений синуса, тангенса, (котангенса) и косеканса дугу берут в пределах от —^π/₂ до ^π/₂ , а для косинуса и секанса в пределах от 0 до π.

Обратные тригонометрические функции называются также обратными круговыми вследствие их связи с кругом.