О ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЯХ.

(ГОНИОМЕТРИЯ.)

IV. Выражение синуса, косинуса и тангенса суммы и разности углов,
двойного угла и половины угла.

§ 50. Синус и косинус суммы и разности двух углов.

Пусть α  и β — положительные  острые углы, составляющие вместе менее 90°.

Отложим в тригонометрическом круге угол α + β (черт. 38). Построим линии  синуса  углов α, β и α + β. Из чертежа  видим, что:

sin α = ^BC/_R;    cos α = ^OC/_R;     sin β = ^FD/_R;    cos β = ^OD/_R;

sin (α + β) = ^FM/_R;    cos (α + β) = ^OM/_R ;

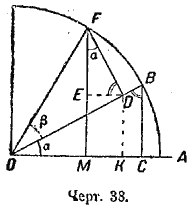
§ 51. а): Синус суммы. Чтобы выразить sin (α + β) через функции углов α  и β , построим треугольники, связывающие тригонометрические линии этих углов. Для этого проведем DE || ОА и DK|| ВС.

Из чертежа получаем, что

FM = EM+EF=KD+ EF.

Чтобы вычислить KD, рассмотрим прямоугольные треугольники ODK и ОВС; они подобны, так как имеют общий острый угол α. Выразим пропорциональность сторон:

^DK/_BC =  ^OD/_OB ;    DK = BC • ^OD/_OB = EM .

Отрезок EF вычислим из прямоугольных треугольников FED и ОВС, которые подобны вследствие перпендикулярности сторон; получим:

^EF/_OC =  ^OFD/_OB ;    EF = OC • ^FD/_OB 

Складывая результаты, получим:

FM = ME + EF=  BC • ^OD/_OB + OC • ^FD/_OB.

Разделим обе части равенства на радиус, чтобы получить отношение отрезков и перейти к тригонометрическим функциям:

^FM/_R =  ^BC/_R • ^OD/_OB + ^OC/_R • ^FD/_OB'

переходя к тригонометрическим функциям, получим:

sin (α + β) = sin α • cos β + cos α • sin β

б) Синус разности (предполагая, что α > β). Чтобы получить синус разности, заменим в предыдущей формуле β на (—β ); получим :

sin [α  + (— β)] = sin α  cos (— β) + cos α  sin (— β);

учитывая, что cos (—β) = cos β; sin (— β) = — sin β, получим:

sin (α — β) = sin α • cos β — cos α • sin β.

§ 52. а) Косинус суммы. Формулу косинуса суммы можно вывести из формулы синуса разности, применяя формулу приведения, а именно:

cos (α + β) = sin [90° — (α + β)];

раскрывая скобки и группируя, получим:

cos (α + β) = sin [(90°— α) — β].

Рассматривая выражение в квадратной скобке как разность углов 90° — α и β и применяя к правой части формулу синуса разности, получим:

cos (α + β) = sin (90° — α) • cos β — cos (90° — α) sin β;

cos (α + β)  = cos α  •  cos β — sin α  •  sin β.

б) Косинус разности. Применим способ замены β на (—β); из предыдущей формулы:

cos [α + (— β)] = cos α • cos (— β) — sin α • sin (— β);

cos (α — β) = cos α • cos β + sin α • sin β.

§ 53. Итак, мы получили следующие четыре формулы:

sin (α + β) = sin α • cos β + cos α • sin β;                      (I)

cos (α + β)  = cos α  •  cos β — sin α  •  sin β;              (II)

sin (α — β) = sin α • cos β — cos α • sin β;                   (III)

cos (α — β) = cos α • cos β + sin α • sin β                    (IV)

При выводе этих формул мы предполагали, что  α > β и что  α + β < 90° ; в следующем параграфе будет доказано, что полученные формулы обладают общностью, т. е. что они справедливы и для каких угодно значений α и β.