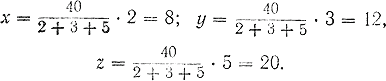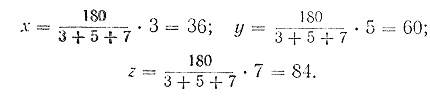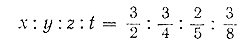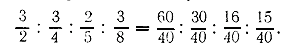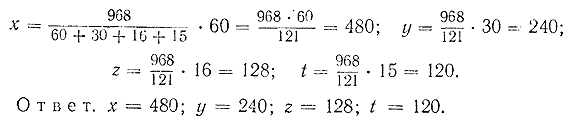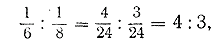Часть  четвёртая.

ПРОПОРЦИИ И ПРОПОРЦИОНАЛЬНОСТЬ ВЕЛИЧИН

Глава   двадцать   первая.

Пропорциональное деление.

§ 138. Деление числа на части прямо пропорционально данным числам
§ 139. Деление числа на части обратно пропорционально данным числам

§ 138. Деление числа на части прямо пропорционально данным числам.

Задача. В саду на двух участках посажено 224 штуки рассады клубники. Определить, сколько штук рассады посажено на каждом участке, если площадь первого участка 8 кв. м, а площадь второго 24 кв. м. (На каждом квадратном метре земли сажают рассаду в среднем поровну.)

Будем решать эту задачу так. Сначала определим площадь двух участков вместе:

8 + 24 = 32 (кв.  м).

Итак, площадь двух участков вместе 32 кв. м. Определим теперь, сколько штук рассады приходится на 1 кв. м:

224 : 32 = 7 (штук).

Зная сколько рассады приходится на 1 кв. м, мы легко вычислим число штук рассады на 8 кв. м и на 24 кв.. м, т. е. ответим на вопрос задачи:

7 • 8 = 56    (штук);  

 7 • 24 = 168  (штук).

Подумаем теперь, какие величины входят в нашу задачу и как они связаны между собой. В условие задачи входят две величины: 1) количество штук рассады, 2) площадь участка. Эти две величины прямо пропорциональны одна другой, потому что, чем больше площадь участка, тем больше на нём можно посадить рассады. Расположим числа, с которыми мы имели дело в задаче, так, чтобы их удобно было сравнивать:

8 кв. м   —   56 штук
24 кв. м — 168 штук

Из этой таблички видно, что второй участок втрое больше первого и рассады на нём в три раза больше, чем на первом.

Итак, в этой задаче мы разделили число штук рассады пропорционально площадям двух участков. Это и есть одна из возможных задач на пропорциональное деление. Как же решаются такие задачи? В задаче требовалось число 224 разделить на две части, пропорциональные числам 8 и 24, т. е. разделить это число на такие две части, которые относились бы между собой так же, как 8 : 24. Обозначим величину первой части буквой х, а второй части — у и напишем отношение этих частей:

Для нахождения этих частей были выполнены следующие действия. Число 224 разделили на сумму чисел 8 и 24 и затем найденное частное последовательно умножили сначала на 8, а потом на 24, т. е.

Словами эти равенства можно высказать так: чтобы разделить некоторое число на части пропорционально данным числам, надо разделить его на сумму этих чисел и полученное частное последовательно умножить на каждое из этих чисел.

Рассмотрим другую задачу: «За три куска мыла одного и того же сорта заплатили 40 руб, Сколько заплатили за каждый из них, если первый кусок весил 2 кг, второй 3 кг и третий 5 кг?»

В этой задаче требуется разделить 40 руб. на 3 части пропорционально весу отдельных кусков мыла. Обозначим стоимость первого куска буквой х, второго куска — у и третьего — z.

Воспользуемся правилом, выведенным при решении первой задачи. Согласно этому правилу для нахождения искомых чисел необходимо число, подлежащее делению, разделить на сумму данных чисел и полученное частное умножить последовательно на каждое из них. Следовательно:

Таким образом, первый кусок мыла стоит 8 руб., второй 12 руб. и третий 20 руб. Найденные числа рублей х, у, z находятся между собой в таких же отношениях, как и данные в задаче числа весовых единиц, т. е.

х : у : z = 8 : 12 : 20 = 2 : 3 : 5.

Рассмотрим теперь задачу с отвлечёнными числами. Разделить число 180 на три части пропорционально числам 3; 5; 7. Иными словами: в этой задаче требуется разложить число 180 на такие три слагаемых, чтобы первое относилось ко второму, как 3 к 5, второе относилось к третьему, как 5 к 7 и, наконец, первое к третьему, как 3 к 7. Сокращённо это можно написать так:

х : у : z = 3 : 5 : 7,

где х, у, z обозначают соответственно  первое,   второе и третье число.

Содержание этой задачи можно пояснить ещё так: требуется разложить число 180 на 3 числа так, чтобы первое число содержало три части (три доли, три пая), второе — пять таких же частей и третье — семь таких же частей.

Применяя указанное выше правило, можем написать:

Полученные три   числа   удовлетворяют  условию задачи:  они в сумме составляют 180, т. е.

36 + 60 + 84 = 180  и   3 : 5 : 7 = 36 : 60 : 84.

Мы решили три задачи на пропорциональное деление.   Покажем теперь другие способы решения таких задач.

Задача 1. Определить квартирную плату за каждую из двух комнат (8 кв. м и 24 кв. м), если за обе вместе нужно заплатить 64 руб.

Обозначим плату за 1 кв. м буквой х; тогда за первую комнату нужно будет заплатить   8x, а за вторую — 24x. Значит, за обе комнаты вместе надо заплатить 8х + 24х, что составляет 64 руб. Следовательно, можно записать равенство:

8х + 24х = 64.

Отсюда:

32x= 64;

х = 64 : 32 = 2 (руб.).

Дальше задача решается так:

2 • 8 = 16 (руб.);   

 2 • 24 = 48 (руб.).

Задача 2. Найти стоимость каждого из трёх пакетов муки, если все три пакета стоят 40 руб., а вес первого 2 кг, второго 3 кг и третьего 5 кг.

Обозначим цену одного килограмма буквой х, тогда:

2  кг будут стоить 2х ;

3 кг     »             »   3х;

5 кг     »              »  5х;

а вся мука будет стоить:

2х + 3х + 5х = 40.

Отсюда:

10х = 40;        х = 40 : 10 = 4 (руб.).

После этого легко определить стоимость каждого пакета;

2х = 2 • 4 = 8    (руб.);

3х = 3 • 4 = 12 (руб.);

5х = 5 • 4 = 20 (руб.).

Задача 3. Разделить число 1 800 на три слагаемых пропорционально числам: 3, 5 и 7.

Рассуждаем так: в первом слагаемом 3 части,   во  втором 5 и в третьем 7.

Обозначая величину одной части буквой х, можно написать:

3х + 5х + 7х =1 800.

Отсюда:

15х = 1 800;              х = 1 800 : 15 = 120.

Следовательно:

3х = 3 • 120 = 360;

5х = 5 •120 = 600;

7х = 7 • 120=840.

Решим теперь задачу, в которой "некоторое число придётся разделить на четыре части пропорционально дробным числам.

Задача. Разделить 968 на четыре части   пропорционально числам: ²/₃ , ³/₄ ,  ²/₅ и ³/₈.Это значит, что надо найти четыре таких числа (х, у, z, t), отношения которых  были бы равны  соответствующим отношениям данных чисел, т. е.

а сумма x + y + z + t = 968.

Заменим отношения дробных чисел отношениями целых чисел, для чего приведём эти дроби к общему знаменателю:

Отбрасывая общий знаменатель 40, получим:  60 : 30 : 16 : 15. Вычислим последовательно каждое из искомых чисел:

§ 139. Деление числа на части обратно пропорционально данным числам.

Теперь перейдём к решению задач, в которых придётся некоторое  число  делить  обратно  пропорционально   данным  числам.

Задача. В двух полевых бригадах 70 колхозников. Каждой бригаде поручено обработать одинаковые участки. Сколько колхозников в каждой бригаде, если первая бригада выполнила работу в 6 дней, а вторая — в 8 дней? (Предполагается, что все колхозники   работают   с   одинаковой   производительностью   труда.)

Очевидно, мы не имеем права делить число колхозников на две части пропорционально времени, которое каждая бригада употребила на работу, так как та бригада, которая быстрее окончила свою работу, была, по-видимому, более многочисленная, чем другая. Поэтому решать эту задачу так же, как мы решали предыдущие задачи, нельзя.

Будем рассуждать следующим образом. Первая бригада колхозников окончила свою работу в 6 дней; значит, в один день  она выполняла ¹/₆ часть всей работы; вторая бригада окончила такую же работу в 8 дней, значит в один день она выполняла ¹/₈ всей работы.

Сравним теперь работу, которую выполняет в день первая бригаду с работой, выполняемой в день второй бригадой. Эти работы выражаются дробями ¹/₆ и ¹/₈. Первая дробь больше второй. Значит, первая бригада в один день может делать больше, чем вторая. А так как все колхозники работают с одинаковой производительностью труда, то, значит, в первой бригаде больше колхозников, чем во второй. Таким образом, число колхозников в каждой бригаде пропорционально той работе, которую каждая бригада может выполнить. Значит, данное в задаче число 70 мы должны   разделить   на две части пропорционально числам: ¹/₆ и ¹/₈  .  С задачами такого типа мы уже знакомы. Приведя дроби ¹/₆ и ¹/₈ к общему знаменателю, мы найдём числа, пропорционально которым следует разделить  число 70:

т. е. число 70 нужно разделить на две части пропорционально числам 4 и 3. Обозначим число колхозников первой бригады буквой х, а второй — буквой у и вычислим:

Итак, в первой бригаде было 40 человек, а во второй 30. Рассмотрим теперь метод   решения этой задачи.   В условие задачи входят три числа: 70 (человек), 6 (дней) и 8 (дней).  В процессе решения мы ввели еще два числа: ¹/₆ и ¹/₈, и пропорционально этим дробям разделили число 70 на две части.  Очевидно, что число 6 и число ¹/₆  взаимно обратны. Так же взаимно сбратны числа 8 и  ¹/₈ .

Для решения задачи требуется разделить 70 рабочих   на две неравные бригады, исходя из количества времени   (дней), затраченного ими на работу. Это время выражается числами 6 (дней) и 8 (дней). Вместо этих двух чисел мы берём обратные  им  числа ¹/₆ и ¹/₈ и пропорционально им делим число 70.

Такая замена сделана нами потому, что число работников не прямо, а обратно пропорционально времени, затраченному на работу. О такой задаче принято говорить, что в ней число 70 разделено на две части обратно пропорционально числам 6 и 8, т. е. в ней первая часть относится ко второй не как 6 к 8, а как 8 к 6.

Итак, чтобы разделить число на части обратно пропорционально данным числам, нужно это число разделить прямо пропорционально обратным числам.

Задача. Разделить 65 на три части обратно пропорционально числам: 2, 3, 4.

Мы теперь знаем, что разделить число на части обратно пропорционально нескольким числам — это значит разделить его на столько же частей прямо пропорционально обратным числам.

Напишем числа, обратные данным в задаче:

данные числа 2, 3, 4;

обратные числа ¹/₂, ¹/₃ , ¹/₄.

Пропорционально этим последним и нужно разделить число 65. Приведём дроби к общему знаменателю:

а  потом освободимся от него:

6 : 4 : 3.

Значит, число 65 нужно разделить   на три части   пропорционально числам 6 : 4 : 3.

Обозначим первую часть буквой х, вторую часть буквой у, третью часть буквой z.  Тогда