|
Г л а в а П. Решение косоугольных треугольников
§7(41). Теорема тангенсов
Теорема. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:
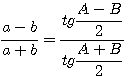
(и две аналогичные формулы для прочих пар сторон а, с и b, с).
Доказательство. В силу теоремы синусов имеем:
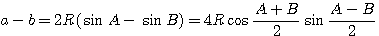
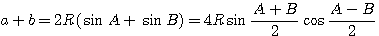
Разделив почленно эти равенства, получим доказываемую формулу.
§8(42). Решение треугольника по двум его углам и стороне
Задача. Даны два угла треугольника и сторона, прилежащая к ним; вычислить другие стороны и угол.
Даны В, С и а; требуется найти b, с и А.
Решение. Условие возможности построения треугольника по этим данным:
А + В < 180°— будем считать выполненным.
Можно считать известными все три угла, так как А = 180° — (В + С).
Для вычисления сторон b и с достаточно применить теорему синусов:
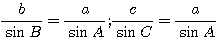 , откуда , откуда 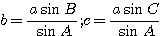
Площадь вычисляется по формуле: 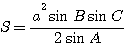
Пример. Решить треугольник по следующим данным а ≈ 17,4, В ≈ 44°30', С ≈ 64°.
Решение при помощи натуральных таблиц. Находим угол:
А = 180° — (В + С) ≈ 180° — (44°30' + 64°) ≈ 71°30'.
Вычисляем стороны. Имеем|
sin В ≈ 0,7009; sin С ≈ 0,8988, sin А ≈ 0,9483
и далее

Деление на sin А можно заменить умножением на обратное число. По таблицам Брадиса (см. табл. II) найдем: 1/0,9483 ≈ 1,055.
Вычисления выполнены по правилам приближённых вычислений. Значения синусов взяты из таблиц Брадиса; во всех промежуточных результатах сохраняются четыре значащие цифры (правило запасной цифры), а окончательный результат округлён до трёх значащих цифр.
Решение при помощи логарифмических таблиц. Имеем:
b = a sin B/sin A, lg b = lg a + lg sin В — lg sin A.
По таблицам найдем:

По таблицам Брадиса найдём b = 12,86. Однако в ответе следует оставить три значащие цифры, так как значение а дано с тремя значащими цифрами; поэтому b ≈ 12,9.
Сторона с вычисляется аналогично:
c = a sin C/sin A, lg c = lg a + lg sin C — lg sin A.
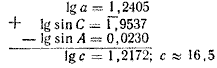
§9(43). Решение треугольника по двум сторонам и углу между ними
Задача. Даны две стороны треугольника и угол между ними; вычислить третью сторону и два других угла.
Пусть, например, даны а, b и С, требуется вычислить А, В и с.
Решение при помощи натуральных таблиц. Формула косинусов даёт выражение стороны с непосредственно через известные элементы:
с = \/ а2 + b2 — 2ab cos С
Для вычисления А можно также воспользоваться формулой косинусов:
а2 =b2 + с2 — 2bc cos А
Так как 0 < А < 180°, то
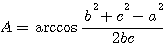 ; ; 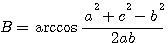
(ясно, что достаточно найти лишь один из углов, третий же угол легко определить исходя из суммы углов треугольника).
Решение при помощи логарифмических таблиц.
Известна сумма углов A + В = 180° — С, откуда (A+C)/2 = 90° — C/2.
Разность углов A — В можно вычислить, воспользовавшись теоремой тангенсов:
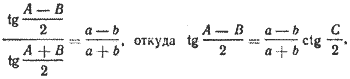
Углы А и В определяются из системы уравнений:
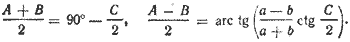
Сторону с можно вычислить по теореме синусов:
c = a sin C/sin A
Пример. Дано: а ≈ 49,4; b ≈ 26,4; С ≈ 47°20'; найти А, В и с.
Решение при помощи натуральных таблиц. Имеем:
с2 = а2 + b2 — 2ab cos С ≈ 49,42 + 26,42 — 2 • 49,4 • 26,4 • cos 47°20'
По таблицам квадратов найдём:
а2 ≈ (49,4)2 ≈ 2449; b2 ≈ (26,4)2 ≈ 697,0
и далее
2 • 49,4 • 26,4 • cos 47°20' ≈ 2 • 49,4 • 2,64 • 0,6778 ≈ 1768.
Следовательно, с2 ≈ 2440 + 697 — 1768 ≈ 1369. По таблицам квадратных корней
с ≈ 37,0. Далее
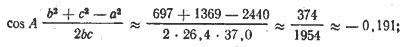
А ≈ arc cos (—0,191); угол А — тупой.
Находим дополнительный угол
180° — А ≈ arc cos (0,091) ≈ 79°; А ≈ 180° — 79° = 101°
(с округлением до 10'). Наконец,
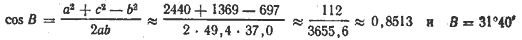
Решение при помощи логарифмических таблиц. Вычислим углы A и В.

Из системы уравнений
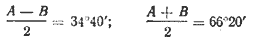
найдём: A ≈ 101°, В ≈ 31°40'.
§ 10 (44). Решение треугольника по двум сторонам и углу,
противолежащему одной из них
Задача. Даны две стороны треугольника и угол А, лежащей против одной из них; вычислить третью сторону и два остальных угла.
Пусть даны a, b и А; требуется вычислить B, С и с
Решение.
|
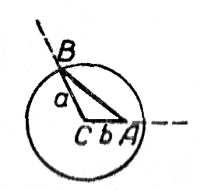
С л у ч а й 1. а > b, т. е, заданный угол А лежит против большей стороны.
Построение показано на чертеже. Из точки С (как из центра), взятой на одной из сторон угла А на расстоянии b от вершины, описана окружность радиуса а; точка В есть точка пересечения этой окружности с другой стороной угла А.
Построение всегда возможно, задача имеет единственное решение.
|
|
|
Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:
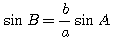
|
|
откуда 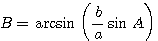
|
|
и затем С = 180° — (A + В). Сторона с находится по теореме синусов: 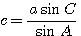
|
|
С л у ч а й 2. а < b, т. e. угол A лежит против меньшей стороны; поэтому он не может быть тупым или прямым.
Следовательно, при А > 90° задача не имеет решения.
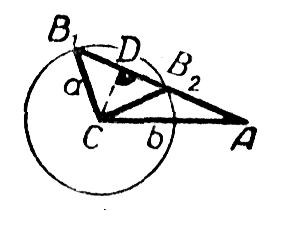
Пусть угол А острый. Из построения на чертеже a) , видно, что окружность радиуса а с центром в точке С пересечёт другую сторону угла А в двух точках при условии а > CD, где D — основание перпендикуляра, опущенного из точки С на другую сторону угла A. Так как CD = b sin
A (из треугольника
ACD),
то условие запишется так: a >b sinA. Для угла В возможны два значения: В
= В1 (острый) и В = В2 (тупой). Задача имеет два решения.
|
a)
|
|
Значения угла В вычисляются по теореме синусов: 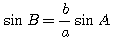
откуда 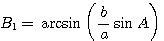 и B2 = 180° - B1 Значения угла С и стороны с вычисляются так же, как в предыдущем случае. и B2 = 180° - B1 Значения угла С и стороны с вычисляются так же, как в предыдущем случае.
|
|
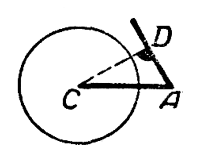
Из чертежа b) видно, что при
CD = b sin А > а окружность не пересечёт другой стороны угла А; задача не имеет решений.
В этом случае 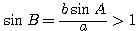 и угол В вычислить нельзя. и угол В вычислить нельзя.
При CD = b sin А задача имеет единственное решение: треугольник ABC прямоугольный.
|
b)
|
|
Случай 3. а = b. В этом случае треугольник ABC равнобедренный. Такой треугольник можно решить, разбразбив его высотой CD на два прямоугольных треугольника:
В = А; С = 180° — 2А; с = 2AD = 2а cos A.
|
Пример. Вычислить стороны и углы треугольника, если дано:
а ≈ 73,5; b ≈ 86,4; A ≈ 49°0'.
Решение:
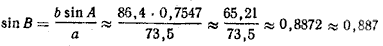
(деление на 73,5 можно заменить умножением на 1/73,5 ≈ 0,0136, табл. 11).
Так как в данном случае а < b и b sin A/a < 1, то задача имеет два решения:
1) В1 ≈ arc sin 0,887 = 62°30'; C1 ≈ 180° — (49° + 62°30') = 68°30'
(с округлением до 10');
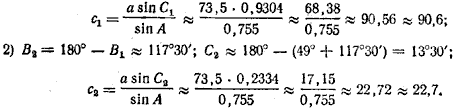
§11(45). Решение треугольника по трем сторонам
Задача. Даны три стороны треугольника; вычислить его углы.
Пусть даны длины трёх сторон треугольника. Обозначим через а меньшую сторону, через b — среднюю, а через с — большую: а < b < с.
По трём данным сторонам можно построить единственный треугольник, если большая сторона меньше суммы двух других сторон: с < а + b. Если же с > а + b, то треугольник с данными сторонами не существует. Будем считать, что с < а + b.
Решение при помощи натуральных таблиц.
Углы треугольника можно вычислить по теореме косинусов: а2 =b2 + с2 — 2bc cos А
b2 =c2 + a2 — 2ca cos B, откуда
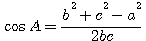 и и 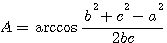 (так как 0°< А <180°). (так как 0°< А <180°).
Аналогично найдём: 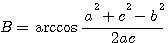 и, наконец, С =180°— (А + В). и, наконец, С =180°— (А + В).
Решение при помощи логарифмических таблиц. Вычислим сначала площадь треугольника (формула Герона):
S = \/р (р — а)(р — b) (р — с) , где р = (а+ b+c)/2
Имеем далее: S = 1/2 bc sin A. откуда 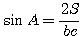
Угол А острый, так как он лежит против меньшей стороны; следовательно,
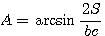
Точно также 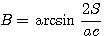 и, наконец, С = 180° — (А + В) и, наконец, С = 180° — (А + В)
Итак, при решении треугольника по трём сторонам при помощи логарифмических таблиц углы, лежащие против меньших сторон, находятся по формулам, а угол, лежащий против наибольшей стороны, вычисляется как разность между 180е и суммой двух найденных углов.
Пример. Решить треугольник, зная длины (приближенные) его сторон: 24,7; 22,4 и 31,3. Обозначим a ≈ 22,4; b ≈ 24,7; с ≈ 31,3.
Решение при помощи натуральных таблиц. Имеем:
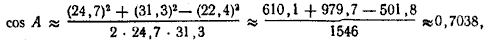
откуда А ≈ 45°20' (с округлением до 10').
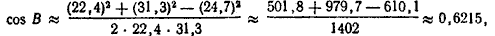
откуда В ≈ 51°30' и, наконец, С ≈ 180° — (45°20' + 51°30') ≈ 83°10'.
Решение при помощи логарифмических таблиц. Имеем:
sin А = 2S/bc, lg sin А = lg 2S — lg b — lg c.
Вычисляем:
lg 2S = lg 2\/р (р — а)(р — b) (р — с) =
= lg2 + 1/2 lg p +1/2 lg ( p—a) + 1/2 lg (p—b) + 1/2 lg(p—c),
где

УПРАЖНЕНИЯ
Решить косоугольные треугольники по заданным основным элементам. (Решение каждого примера следует выполнить при помощи таблиц логарифмов и логарифмической линейки.)
81 (347). Даны сторона и два угла:
1) а ≈ 370,0; В ≈ 86°30'; С ≈ 50°50'
2) а ≈ 450,0; А ≈ 87°50'; В ≈ 10°50'.
3) а ≈ 951; B ≈ 126°40'; С ≈ 13°20'.
4) b ≈ 13,02; A ≈ 11°46'; B ≈ 133°40'.
82 (348). Даны две стороны и угол между ними:
1) а ≈ 510; b ≈ 317; С ≈ 76°10'.
2) а ≈ 225; b ≈ 800; С ≈ 36°40'.
3) а ≈ 2,296; с ≈ 1,687; В ≈ 29°52'.
4) b ≈ 28; c ≈ 42; А ≈ 124°.
83 (349). Даны две стороны и угол против одной из них:
1) а ≈ 87; b ≈ 65; А ≈ 75°.
2) b ≈ 360; с ≈ 309; С ≈ 21°30'.
3) а ≈ 13,89; с ≈ 8,42; А ≈ 126°41'.
4) а ≈ 13,81; с ≈ 8,14; С ≈ 14°37'.
5) b ≈ 263,1; с ≈ 215,4; В ≈ 70°14'.
6) а ≈ 19,06; b ≈ 88,19; А ≈ 31°17'.
84 (350). Даны три стороны:
1) а ≈ 19; b ≈ 34; c ≈ 49.
2) а ≈ 0,099; b ≈ 0,101; с ≈ 0,158.
3) a ≈ 172,5; b ≈ 113,4; с ≈ 120,5.
4) а ≈ 1,234; b ≈ 2,345; с ≈ 3,457.
85 (351). Решить косоугольные треугольники по заданным моментам:
1) R ≈ 7,92; А ≈ 113°17'; В ≈ 48°16'.
2) S ≈ 501,9; А ≈ 15°28'; B ≈ 45°23'.
3)hа ≈ 5,37; В ≈ 115°10'; С ≈ 5°33'.
4) lа ≈ 0,758; B ≈ 98°30'; С ≈ 4°20'.
5) а + b ≈ 488,8; А ≈ 70°24'; В ≈ 40°16'.
6) a — b ≈ 23; А ≈ 108°; B ≈ 18°.
7) r ≈ 5,0; А ≈ 22°; В ≈ 39°.
8) S ≈ 2420; а ≈ 42,5; B ≈ 124°50'.
9) а ≈ 32; b ≈ 25; A ≈ 2В.
10) S ≈ 15; аb ≈ 48; sin А ≈ соs В.
11) а ≈ 120,0; b ≈ 29,0; hа ≈ 23,7.
12) hа ≈ 8; h ≈ 12; hа ≈ 18.
ОТВЕТЫ
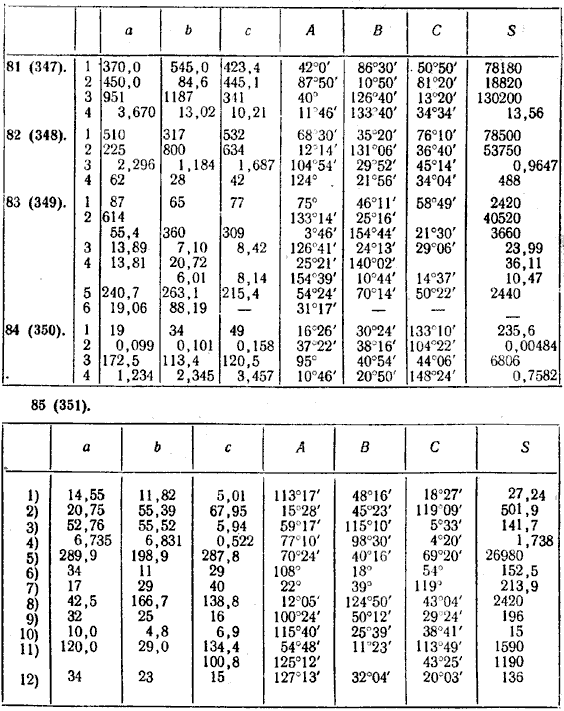
|