|
9.СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ.
|
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОСТРОГО УГЛА.
|
|
На основании равенства и подобия треугольников мы имели возможность решить ряд задач, связанных с определением расстояний, измерить которые непосредственно не представлялось возможным. Например, мы находили расстояние до недоступной точки, высоту предметов, расстояние между пунктами, разделёнными каким-нибудь препятствием, и т. д.
Такие работы имеют большое практическое значение, однако при их выполнении мы получали недостаточно точные результаты. Если результаты, полученные нами, могли удовлетворять нас,когда мы имели дело с фигурами небольших размеров, то они совершенно не могли бы удовлетворить нас в силу своей неточности, если бы мы имели дело с фигурами, имеющими большие размеры. Кроме того, без угломерного инструмента мы не в состоянии были находить размеры углов, имея в своём распоряжении только
лишь
длину тех или иных отрезков; например, по длине сторон произвольного треугольника мы не могли определять величину его углов.
Однако в математической науке существуют такие приёмы, которые обеспечивают необходимую точность измерений, несмотря на значительные размеры избранных для измерения расстояний, а кроме того, дают возможность по длине тех или иных отрезков определять размеры нужных нам углов и длины неизвестных отрезков.
Овладение такими приёмами связано с изучением так называемых тригонометрических функций. К ознакомлению с некоторыми из них мы и переходим.
|
|
1.ОПРЕДЕЛЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
|
|
1.1. Соответствие между отношением сторон и величиной острых углов в прямоугольном треугольнике.
|
|
Пусть имеется какой-нибудь произвольный острый угол, например / ВАС = а . На стороне AB возьмём произвольную точку М и опустим из неё перпендикуляр MN на сторону АС. Получим прямоугольный треугольник MAN.
|
 |
|
Возьмём отношения его сторон попарно:
|
MN
AM |
(отношение катета, противолежащего углу а, к гипотенузе);
|
AN
AM |
(отношение катета, прилежащего к углу а, к гипотенузе);
|
MN
AN |
(отношение катета, противолежащего углу а, к катету прилежащему);
|
AM
MN |
(отношение гипотенузы к катету, противолежащему углу а);
|
AM
AN |
(отношение гипотенузы к катету, прилежащему к углу а);
|
AN
MN |
(отношение катета, прилежащего к углу а, к катету противолежащему).
|
|
Мы получили 6 отношений. Величина этих отношений не зависит от того, где на стороне АВ мы возьмём точку М. Так, если вместо точки М мы возьмём на стороне АВ какую-нибудь точку М' , то новый треугольник AM'N' будет подобен треугольнику MAN и потому ни одно из отношений не изменится.
Значит, взятому углу а соответствуют одни и те же определённые значения каждого из отношений.
|
|
Возьмём теперь другой острый угол, / В'АС = ß (например, больший угла а), и на стороне А В' отметим точку Р так, чтобы АР = AM . Как увидим ниже, подобный выбор точки Р не повлияет на общность рассуждений. Опустив из точки Р перпендикуляр PD на сторону АС, получим прямоугольный треугольник APD |
 |
|
Составим отношения сторон этого треугольника в том же порядке, как и для треугольника MAN:
|
PD
AP |
AD
AP |
PD
AD |
AP
PD |
AP
AD |
AD
PD |
|
Эти отношения не изменятся, если точку Р переместим в любую точку Р' луча АВ'. Значит, взятому значению угла ß соответствует определённое значение каждого из отношений.
|
|
Однако если мы сравним значения соответствующих отношений для угла а и для угла ß, то увидим, что они различны:
|
PD
AP |
 |
MN
AM |
так как АР = AM, a PD > MN;
|
AD
AP |
 |
AN
AM |
так как АР = AM, a AD < AN;
|
PD
AD |
 |
MN
AN |
так как PD > MN и AD < AN и, следовательно,первое отношение больше второго и т. д.
|
|
Таким образом, выходит, что каждому размеру острого угла соответствует определённое значение каждого отношения сторон.
Справедливо и обратное утверждение: каждому значению отношения сторон соответствует определённый размер угла.
На этом основании можно считать, что отношения сторон прямоугольного треугольника являются функциями его острого угла. Эти функции называются тригонометрическими функциями угла.
Перейдём к более подробному их рассмотрению.
1.2. Определение тригонометрических функций.
|
|
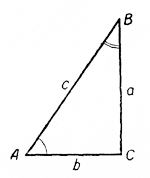
Возьмём прямоугольный треугольник ABC и обозначим его стороны буквами a, b и с . Рассмотрим сначала функции угла А.
|

|
|
Отношение  называется синусом угла А, называется синусом угла А,
т. е. синусом угла А называется отношение катета, противолежащего этому углу, к гипотенузе.
Отношение  называется косинусом угла А, называется косинусом угла А,
т. е. косинусом угла А называется отношение катета, прилежащего к этому углу, к гипотенузе.
Отношение  называется тангенсом угла А, называется тангенсом угла А,
т. е. тангенсом угла А называется отношение катета, противолежащего этому углу, к катету прилежащему.
Отношение  называется котангенсом угла А, называется котангенсом угла А,
т.е. котангенсом угла А называется отношение катета, прилежащего к этому углу, к катету противолежащему.
Отношение  называется секансом угла А. называется секансом угла А.
Отношение  называется косекансом угла А. называется косекансом угла А.
Наиболее употребительными являются первые четыре функции: синус, косинус, тангенс и котангенс.
Эти функции угла A обозначаются так: sin / A, cos / A, tg / A и ctg / A;
 ; ;  ; ;  ; ;  . .
|
|
Установим теперь функции для / В:
|
b
c |
- синус угла В,
|
b
c |
= |
sin / B
|
a
c |
- косинус угла В,
|
a
c |
= |
cos / B
|
b
a |
- тангенс угла В,
|
b
a |
= |
tg / B
|
a
b |
- котангенс угла В
|
a
b |
= |
ctg / B
|
|
Упражнения.
1. Начертить прямоугольный треугольник с катетами 3 см и 4 см. Вычислить с помощью теоремы Пифагора длину гипотенузы, а затем синус, косинус, тангенс и котангенс острых углов треугольника.
2. Начертить прямоугольный треугольник ABC с катетами: АС = 18 мм, ВС= 24 мм, вычислить с помощью теоремы Пифагора длину гипотенузы АВ и найти синус, косинус, тангенс и котангенс угла А, а затем синус, косинус, тангенс и котангенс угла В.
3. Начертить
произвольный прямоугольный
треугольник, измеритьегостороны в миллиметрах и найти синус, косинус, тангенс и котангенс острых углов треугольника с точностью до 0,01.
|
|
2. ПОСТРОЕНИЕ УГЛА ПО ЗАДАННОМУ ЗНАЧЕНИЮ ОДНОЙ ИЗ ЕГО ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.
|
|
2.1. Построить угол, тангенс которого равен 4/5.
|
 |
Построим с помощью чертёжного треугольника прямой угол и на одной его стороне отложим от вершины 5 произвольных масштабных единиц, а на другой - 4 . Соединив точки А и В, получим прямоугольный треугольник ABC.
/ A будет искомым, так как tg / A = 4/5
|
|
2.2. Построить угол, синус которого равен 3/5.
|
|
Построим прямой угол и на одной его стороне отложим от вершины отрезок СВ, равный трём произвольным масштабным единицам . Из точки В, как из центра, радиусом, равным 5 тем же масштабным единицам, опишем дугу, пересекающую другую сторону прямого угла. Точку пересечения обозначим буквой А. Соединив точки А и В, получим прямоугольный треугольник ABC.
/ A будет искомым, так как sin / A = 3/5.
|
 |
|
2.3. Построить угол, косинус которого равен 5/6
|
|
Построим прямой угол и на одной его стороне отложим от вершины угла отрезок АС, равный 5 произвольным масштабным единицам. Из точки А, как из центра, радиусом, равным 6 тем же масштабным единицам, опишем дугу, пересекающую другую сторону прямого угла. Точку пересечения обозначим буквой
В. Соединив точки Аи В, получим прямоугольный треугольник ABC.
/ A будет искомым, так как cos / A = 5/6.
|
 |
|
Так как каждый из катетов прямоугольного треугольника всегда меньше гипотенуаы, то синус и косинус любого острого угла всегда меньше 1.
Что касается сравнительной величины катетов, то каждый из них может быть и больше, и меньше другого. Поэтому tg / A и ctg / A могут быть выражены любим положительным числом. Каждый из них может быть меньше единицы, больше единицы и равен единице.
|
|
3. ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ НЕКОТОРЫХ УГЛОВ.
|
|
Найдём значения тригонометрических функций для углов в 30°, 45° и 60°.
1)Для угла в 30°
Сначала вспомним свойство прямоугольного треугольника с углом в 30°
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы
|
|
Пусть в прямоугольном треугольнике АСВ угол В равен 30° Тогда другой его острый угол будет равен 60°.
Докажем, что катет АС равен половине гипотенузы АВ.
Продолжим катет АС за вершину прямого угла С и отложим отрезок СМ, равный отрезку АС. Точку М соединим с точкой В. Полученный треугольник ВСМ равен треугольнику АСВ .
Мы видим, что каждый угол треугольника АВМ равен 60°, следовательно, этот треугольник - равносторонний. Катет АС равен половине AM, а так как AM равняется АВ, то катет АС будет равен половине гипотенузы АВ.
|

|
|
Переходим к поиску значений тригонометрических функций для угла 30о
|
|
Возьмём прямоугольный треугольник с острым углом в 30°. Обозначим длину гипотенузы АВ через с и выразим длины катетов.
|

|
|
ВС = C/2 , как катет, лежащий против угла в 30°.
|
|
Катет АС найдём по теореме Пифагора.
|
 |
|
Тогда
|
sin30o =  |
tg30o =  |
|
cos30o= 
|
|
2) Для угла в 45°.
|
|
Возьмём прямоугольный треугольник с острыми углами по 45°. Обозначим длину гипотенузы АВ через с и выразим длины катетов. АС = ВС, следовательно, по теореме Пифагора
AB2 = 2BC2, откуда 
|

|
Значит,  ,одновременно и ,одновременно и  |
|
sin 45° = 
|
|
tg 45°= 
|
|
cos 45°= 
|
|
3) Для угла в 60°
|
|
Значения тригонометрических функций для угла в 60° можно найти из того же треугольника, из которого нашли значения тригонометрических функций для угла в 30°, так как если / A = 30°, то / В = 60°.
|
| Тогда |
|
sin 60° = 
|
|
tg 60° = 
|
|
cos 60° = 
|
|
Составим теперь таблицу значений тригонометрических функций для углов в 30°, 45° и 60°.
|
|
УГОЛ
|
СИНУС
|
КОСИНУС
|
ТАНГЕНС
|
|
30о
|

|

|

|
|
45о
|

|

|
1
|
|
60о
|

|

|

|
|
Рассматривая эту таблицу, можно заметить, что синус и тангенс острого угла возрастают при увеличении угла, а косинус при увеличении угла у б ы в а ет.
При уменьшении угла синус и тангенс убывают, а кoсинус возрастает.
|
|
Упражнения.
1. Пользуясь чертежом, рассмотреть изменение тригонометрических функций в связи с изменением угла .
2. Значения тригонометрических функций помещены в математических таблицах В.М.Брадиса подробное описание таблиц и указания к их использованию даны в самих таблицах.
Пользуясь таблицами Брадиса, рассмотреть изменение тригонометрических функций в связи с изменением угла.
|

|
|
4.ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ДОПОЛНИТЕЛЬНЫХ УГЛОВ.
|
|
Дополнительными углами называются два угла, которые в сумме составляют 90°. Такими углами, в частности, являются острые углы прямоугольного треугольника.
|
|
Углы А и В в прямоугольном треугольнике АСВ являются дополнительными углами, так как
/ A + / B = 90°; / A = 90° - / B; / В = 90° - / A.
|
|
|
Рассмотрим соотношения между тригонометрическими функциями дополнительных углов.
1) 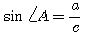 ; ; 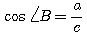 , т. e. cинус данного угла равен косинусу дополнительного угла. , т. e. cинус данного угла равен косинусу дополнительного угла.
|
|
2) 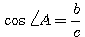 ; ; 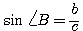 , т.е. косинус данного угла равен синусу дополнительного угла. , т.е. косинус данного угла равен синусу дополнительного угла.
|
|
3) 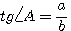 ; ; 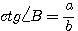 ,т.е. тангенс данного угла равен котангенсу дополнительного угла. ,т.е. тангенс данного угла равен котангенсу дополнительного угла.
|
|
4)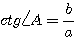 ; ; 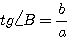 ,т.e. котангенс данного угла равен тангенсу дополнительного угла. ,т.e. котангенс данного угла равен тангенсу дополнительного угла.
|
|
Знание соотношений между тригонометрическими функциями дополнительных углов важно для понимания устройства тригонометрических таблиц.
|
|
5.СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ.
|
|
Пусть дан прямоугольный треугольник ABC. Обозначим его стороны через а, b и с. По определению тригонометрических функций:
|

|
|
a/c = sin / А; a/c = cos / В; b/c= sin / В; b/c == cos / А.
|
|
Отсюда а = с sin / А = с cos / В; b = c sin / B = с соs / A, т. е. катет прямоугольного треугольника равен гипотенузе, умноженной на синус угла, противолежащего этому катету, или на косинус угла, прилежащего к нему.
Из того же прямоугольного треугольника имеем, что a/b = tg / А , отсюда a = b tg / А;
b/a = ctg / А, откуда b = a ctg / А, т.е. катет прямоугольного треугольника равен другому катету, умноженному на тангенс угла, противолежащего первому катету, или на котангенс угла, прилежащего к первому катету.
6.РЕШЕНИЕ ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ.
|
|
Выведенные нами соотношения дают возможность решать прямоугольные треугольники, т. е. по некоторым данным элементам треугольника находить все остальные.
Рассмотрим несколько примеров.
1. Даны гипотенуза прямоугольного треугольника и один из его острых углов. Найти катеты этого треугольника и второй острый угол.
|
|
Пусть гипотенуза с = 82,0 см; / А = 42° . Вычислить длину катетов а и b и величину угла В.
Прежде всего определим величину / B,
/ В = 90o - / А = 90°- 42° = 48°.
Чтобы вычислить длину катета а, найдём по таблицам значение синуса угла в 42°.
sin 42° = 0,6691.
Так как а = с sin / А, получим:
а = 82,0 • 0,6691  54,9 (см). 54,9 (см).
|

|
| (Примечание. В наш век компьютерной техники вовсе не обязательно носиться в поисках математических таблиц, достаточно запустить стандартную встроенную программу "калькулятор", выбрать вид "инженерный" (или программу Excel), и найти значение любой тригонометрической функции для любого угла.) |
|
Второй катет треугольника можно вычислить различными способами. Используя значение угла А, находим: b = с cos 42°, или b = 82,0 • 0,7431  60,9 (см). 60,9 (см).
Все неизвестные элементы треугольника ABC вычислены.
Длину катета b можно найти из равенства b = с sin / В,
т. е. b = c sin 48°.
Пользуясь таблицами квадратов чисел (или встроенным в Windows калькулятором или в Excel), можно также вычислить катет b и на основании теоремы Пифагора:

2. Даны катет прямоугольного треугольника и один из его острых углов. Найти гипотенузу, второй катет этого треугольника и второй острый угол.
|
|
Пусть катет а равен 25 см, угол А равен 32°. Вычислите длину гипотенузы с, длину катета b и величину угла В. / В = 90° - / А = 90° - 32° = 58°;
|

|
|
а = c sin / А, откуда  ; ;  ; ;  (см); (см);
а = b tg / А ;  ; ;  (см) (см)
Все неизвестные элементы треугольника ABC вычислены. Можно было и в данной задаче применить иные способы решения.
Например: b = \/c2-a2  \/ 472 - 252 \/ 472 - 252  40 (cм). 40 (cм).
3. Даны два катета прямоугольного треугольника, найти его гипотенузу и величину острых углов.
|
|
Пусть катет а равен 21 см, а катет b равен 18 см . Вычислить длину гипотенузы с и величину углов А и В.
Найдём сначала (пользуясь теоремой Пифагора и таблицами квадратов чисел или рессурсами компьютерных программ) длину гипотенузы с:
|

|
|
c = \/a2+b2 ; \/ 212 + 182  28 (cм). 28 (cм).
|
|
Найдём величину одного из острых углов, используя равенство
|
|
a/b = tg / А ; tg / А = 21/18  1,1667 1,1667
|
|
Откуда / А  49° (с точностью до 1°), тогда / B 49° (с точностью до 1°), тогда / B  41°. 41°.
4. Даны катет и гипотенуза прямоугольного треугольника. Катет а = 52 см, гипотенуза с = 67 см. Решить треугольник (самостоятельно) .
|
|
7.УГОЛ ПРЯМОЙ С ПЛОСКОСТЬЮ.
|
|
При выполнении различных практических измерительных работ на местности часто приходится использовать углы, образуемые прямой с плоскостью.
|
|
Угол прямой с плоскостью определяется следующим образом. Пусть имеется плоскость и какая-нибудь прямая, пересекающая эту плоскость, например, прямая АВ пересекает плоскость Р в точке А. Чтобы определить угол этой прямой с данной плоскостью, из какой-нибудь точки С прямой А В опустим перпендикуляр СС' на данную плоскость Р.Через точки А и С проведём на плоскости Р прямую АС. / ВАС' и будет углом, образованным прямой АВ с данной плоскостью Р.
|

|
|
8.ПРАКТИЧЕСКИЕ ЗАДАЧИ С ПРИМЕНЕНИЕМ ТРИГОНОМЕТРИИ.
|
|
Знание тригонометрических функций позволяет нам решать практические задачи более совершенными методами и с большей точностью. Рассмотрим несколько таких задач.
|
|
1. Определить высоту предмета, к основанию которого подойти нельзя.
Например, нужно определить высоту телевизионной антенны, которая отделена от нас рекой.
Рассмотрим прямоугольный треугольник ACD. В этом треугольнике мы можем с помощью астролябии измерить угол А. Положим, он равен 42°.
|
|

|
|
В тpeyгольнике BCD измеряем / DBC, пусть он равен 47°.
|
|
Решение.
|
|
 ; ; 
|
|
  (точки A, B, С находятся на одной прямой) (точки A, B, С находятся на одной прямой)
|
|

|

|
|

|
|
Расстояние АС — ВС, т. е. АВ, может быть непосредственно измерено, пусть оно равно 12,0 м, тогда
12,0 = CD(1,1106 — 0,9325) = CD• 0,1781.
|
|
Откуда 
|
|
Для окончательного определения высоты антенны к 67,4 м следует прибавить высоту прибора, с помощью которого определяли углы А и В. Если высота прибора, например, составляла 1,40 м, то окончательно высота антенны будет равна 67,4 + 1,40 = 68,8 (м).
|
|
2. Определить расстояние между пунктами А и В, разделёнными препятствием.
|
 |
а) Пусть требуется найти расстояние от пункта А до пункта В, находящегося за рекой .Строим при помощи астролябии или эккера при точке А прямой угол ВАС, Взяв на прямой АС произвольную точку D, с помощью астролябии измеряем угол ADB; пусть он равен 44°. Измеряем расстояние AD; пусть оно составит 120 м.
Тогда  , или АВ = 120•tg 44o , или АВ = 120•tg 44o  120 • 0,9657 120 • 0,9657  116 (м). 116 (м).
|
|
б) Пусть нужно определить расстояние от пункта А до пункта В, между которыми находится водное пространство.Принимая точку А за вершину угла, строим прямой угол ВАМ. На прямой AM фиксируем какую-нибудь точку С, находящуюся от точки А на расстоянии, например, 200 м. С помощью астролябии определяем угол АСВ. Пусть он будет равен 48°. Тогда
 или или 
Откуда АВ = 1,1106• 200 222 (м). 222 (м).
|
 |
|
9.СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ.
|
|
1)Найдем соотношение между тангенсом и котангенсом.
tgA= a/b ; ctgA= b/a , следовательно
 и наоборот и наоборот 
|

|
|
2)Выразим тангенс и котангенс угла А через синус и косинус.
tgA= a/b ; sinA= a/c ; cosA= b/c отношение
a/b получим, если a/c разделим на b/c :
 , следовательно , следовательно
 , учитывая соотношение между тангенсом и котангенсом, найдем соответствующее выражение и для котангенса: , учитывая соотношение между тангенсом и котангенсом, найдем соответствующее выражение и для котангенса:

3) Найдем значение выражения sin2A + cos2A
|
|
|
|
 , но по теореме Пифагора a2 + b2 = c2,следовательно , но по теореме Пифагора a2 + b2 = c2,следовательно
|
|
sin2A + cos2A = 1
|
|
4) Докажем , что 

|
|
Аналогично можно доказать, что

|
| |
| |
| |
|




 называется синусом угла А,
называется синусом угла А,  называется косинусом угла А,
называется косинусом угла А,  называется тангенсом угла А,
называется тангенсом угла А,  называется котангенсом угла А,
называется котангенсом угла А, называется секансом угла А.
называется секансом угла А. называется косекансом угла А.
называется косекансом угла А. ;
;  ;
;  ;
;  .
.










 ,одновременно и
,одновременно и 













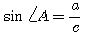 ;
; 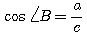 , т. e. cинус данного угла равен косинусу дополнительного угла.
, т. e. cинус данного угла равен косинусу дополнительного угла.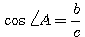 ;
; 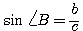 , т.е. косинус данного угла равен синусу дополнительного угла.
, т.е. косинус данного угла равен синусу дополнительного угла.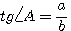 ;
; 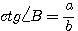 ,т.е. тангенс данного угла равен котангенсу дополнительного угла.
,т.е. тангенс данного угла равен котангенсу дополнительного угла.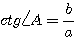 ;
; 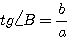 ,т.e. котангенс данного угла равен тангенсу дополнительного угла.
,т.e. котангенс данного угла равен тангенсу дополнительного угла.
 54,9 (см).
54,9 (см).


 ;
;  ;
;  (см);
(см); ;
;  (см)
(см)


 ;
; 

 (точки A, B, С находятся на одной прямой)
(точки A, B, С находятся на одной прямой)




 , или АВ = 120•tg 44o
, или АВ = 120•tg 44o  или
или 

 и наоборот
и наоборот 
 , следовательно
, следовательно , учитывая соотношение между тангенсом и котангенсом, найдем соответствующее выражение и для котангенса:
, учитывая соотношение между тангенсом и котангенсом, найдем соответствующее выражение и для котангенса:
 , но по теореме Пифагора a2 + b2 = c2,следовательно
, но по теореме Пифагора a2 + b2 = c2,следовательно

