|
ГЛАВА 9
РАЗНЫЕ ЗАДАЧИ
Разные задачи
942. Угол между двумя соседними лучами равен 2π/n. Обозначим через d1, d2, ... расстояния от А до оснований перпендикуляров, последовательно опускаемых на лучи, исходящие из точки А (рис. 7).
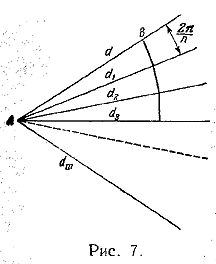
Очевидно, имеем:
dk = d (cos 2π/n)k ( k = 1,2, ...)
Длина k-го перпендикуляра равна
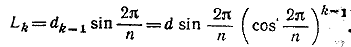
Полная длина ломаной из т звеньев будет
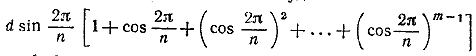
Длина L бесконечно завивающейся ломаной получится при неограниченном увеличении т и выразится суммой членов бесконечной убывающей геометрической прогрессии со знаменателем q = cos2π/n и первым членом d sin2π/n:
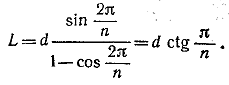
При увеличении n длина L, растет и при неограниченном увеличении п растет неограниченно.
__________________________________________________
943. Первое решение. Пусть 1abcde — искомое число (здесь буквы а, b, с, d, e обозначают цифры соответствующих разрядов).
Очевидно, е = 7, так как 1abcde • 3 = abcde1.
После умножения 7 на 3 двойка переходит в следующий разряд, поэтому произведение d • 3 должно оканчиваться цифрой 5. Значит, d = 5. Имеем 1аbс57 • 3 = аbс571. Рассуждая аналогично, находим, что с =8, b = 1 и, наконец, а = 4. Искомое число есть 142 857.
Второе решение. Пусть снова 1abcde—искомое число. Положим abcde = x, тогда искомое число равно 105 + x . По условию задачи имеем
(105 + x) • 3 =10x +1,
откуда x = 42 857. Следовательно, искомое число 142 857.
__________________________________________________
944. Так как р делится на 37, то можно написать
р =100a +10b + c =37k, где k—целое.
Очевидно, далее, что
q = 100b + 10с + а = 10р — 999а = 370k — 37•27а.
Следовательно, и q делится на 37.
Аналогичные рассуждения пригодны и для числа r.
__________________________________________________
945. Имеем: А = п3 + (п + 1)3 + (п + 2)3 = 3п3+9п2 +15п + 9.
Очевидно, достаточно показать, что В = 3п3 + 15п = 3п(п2+ 5) делится на 9.
Если п =3k, k — целое, то В делится на 9.
При п = 3k + l , п2 + 5 = 9k2 + 6k + 6;
при п = 3k + 2, п2 + 5 = 9k2 + 12k + 9. В обоих случаях п2 + 5 делится на 3. Следовательно, во всех случаях В делится на 9.
__________________________________________________
946. Первое решение. Сумму Sn можно представить в следующем виде
Sn = п3 + 3(п2 + 2п + l) — п = (п—1) • п • (п + 1) + 3(п+1)2 .
Первое слагаемое делится на 3, так как оно является произведением трех последовательных целых чисел (одно из них обязательно кратно трем). Следовательно, и Sn делится на 3.
Второе решение. Доказательство проведем по индукции. При п = 1 S1 =12 делится на 3. Допустим, что при каком-либо п сумма Sn делится на 3. Имеем:
Sn+1 = (п + l )3 + 3(п + l )2 + 5 (п + l ) +3 = Sn + 3(п2 + 3п + 3). Следовательно, Sn+1 также делится на 3.
__________________________________________________
947. В основании пирамиды шары уложены в виде равностороннего треугольника. Пусть сторона этого треугольника содержит п шаров. Тогда в основании пирамиды лежит
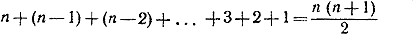 шaров. шaров.
Следующий, второй слой пирамиды содержит
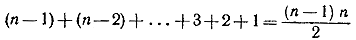 шаров. шаров.
Третий слой пирамиды содержит 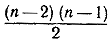 шаров и т. д. шаров и т. д.
Последний, самый верхний, слой состоит из одного шара. Всего в пирамиде 120 шаров. Следовательно,

Правая часть равенства равна  (см. задачу 923), следовательно, для определения п получаем уравнение (см. задачу 923), следовательно, для определения п получаем уравнение
п(п+ 1) (п+ 2) = 720. (1)
Это уравнение имеет очевидное решение п = 8. Для отыскания других решений этого уравнения переносим 720 в левую часть и получающийся там многочлен делим на п — 8. Частное от деления будет равно п2+11п + 90. Так как корни этого последнего многочлена невещественны, то уравнение (1) не имеет других целых решений, кроме п = 8. Итак, в основании
пирамидальной фигуры лежит 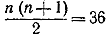 шаров шаров
__________________________________________________
948. Так как число наполненных ящиков равно т, то число вложенных ящиков будет равно mk. Отсюда вытекает, что количество всех ящиков (вместе с первым) равно mk+1. Следовательно, число пустых ящиков равно mk +1— m = m(k —1) + 1.
__________________________________________________
|