|
2. Пусть AD — биссектриса прямого угла А в /\ АВС и DE _|_ АС (рис. 9).
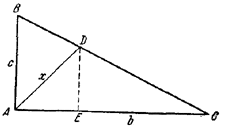
Рис. 9.
Так как
/ DAE = π/4, то АЕ = DЕ = x/√2
где x = AD — искомая длина. Очевидно,
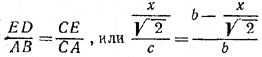
Отсюда
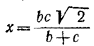
________________________________________________
3. В треугольнике ABC (рис. 10) О есть точка пересечения медиан AD и BE; AC = b, ВС = а. Найдем АВ = с.
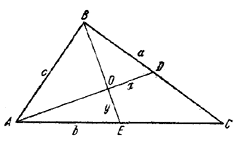
Рис. 10.
Пусть OD = x; ОЕ = у. Используя свойство медиан, из треугольников АОВ, BOD и АОЕ найдем:
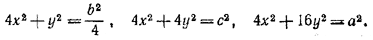
Исключив х и у, получим:
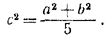
Условия существования треугольника со сторонами а, b, с принимают вид
5 (а + b)2 > а2 + b2, 5 (а — b)2 < а2 + b2.
Первое неравенство, очевидно, выполнено при любых а и b, а второе преобразуется в следующее:
а2 — 5/2 ab + b2 < 0.
Решив это неравенство относительно a/b , окончательно получим:
1/2 < a/b < 2
________________________________________________
4. Пусть / AСD = / DCE = / EСВ = α и СЕ = х, CD = y (рис. 11).
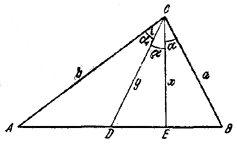
Рис. 11
Для площади треугольника ABC можно написать следующие три выражения:
SACD+ SDCB = 1/2 by sin α + 1/2 ay sin 2α,
SACЕ + SЕCB = 1/2 bx sin 2α + 1/2 ax sin α ,
SACD + SDCЕ + SЕCB = 1/2 by sin α + 1/2 xу sin α + 1/2 ax sin α.
Приравнивая друг другу левые части этих равенств и учитывая условие задачи, придем к системе трех уравнений:
2a cos α = х + а x/y ,
2b cos α = y + b y/x ,
x/y = m/n
Решив ее, получим:
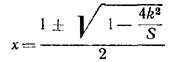
________________________________________________
5. Обозначим через S площадь данного треугольника ABC (рис. 12) и положим AD/AB = x
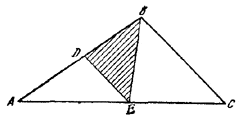
Рис.12
Тогда площадь /\ ADE будет равна x2S, а площадь /\ ABE равна xS. Условие задачи приводит к уравнению
xS — x2S = k2,
решив которое, получим:
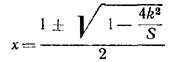
Задача разрешима, если S > 4k2, и имеет два или одно решение в зависимости от того, будет ли S > 4k2 или S = 4k2 соответственно.
________________________________________________
6. Обозначим через S площадь данного треугольника ABC. Полученные указанным в условии задачи построением треугольники с площадями S1, S2, S3 подобны /\ ABC (рис.13).
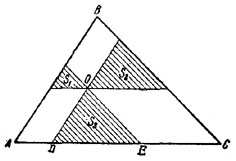
Рис.13.
Поэтому их площади относятся как квадраты сходственных сторон, откуда
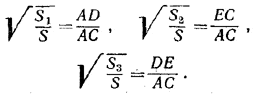
Сложив эти равенства почленно, найдем:
S = ( √S1 + √S2 + √S3 )2
________________________________________________
7. Третью сторону треугольника, равную опущенной на нее высоте, обозначим через х. Используя два выражения для площади данного треугольника, получим уравнение
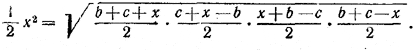
Решив его, найдем:
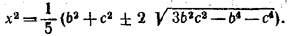 (1) (1)
Необходимым условием разрешимости задачи является условие
3b2c2 > b4 + с4. (2)
Если оно выполнено, то оба значения х2 в (1) положительны. Легко проверить, что при выполнении (2) будут также выполнены неравенства
b + с > х > |b — с | ,
причем знак равенства имеет место только в том случае, когда x = 0. Последнее имеет место, если в (1) при b = с взять перед корнем знак минус. Следовательно, в случае b = с задача имеет единственное решение
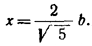
Если b =/= с, то треугольник существует лишь в том случае, когда выполнено неравенство (2). Решив его относительно b/c , найдем, что оно эквивалентно следующим неравенствам:
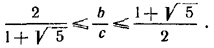 (3) (3)
Следовательно, при b =/= с существуют два треугольника, если оба неравенства (3) выполнены со знаком <, и один треугольник, если хотя бы одно из неравенств (3) выполнено со знаком =.
________________________________________________
8. Сначала предположим, что /\ ABC остроугольный (рис. 14).
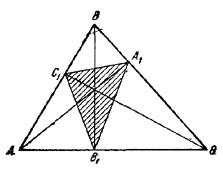
Рис.14.
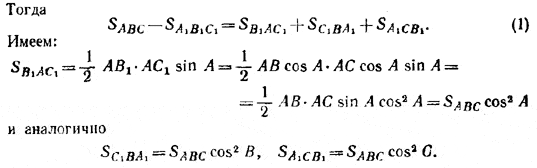
Подставив эти выражения в (1), после очевидных преобразований получим:
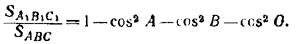 (2) (2)
Если /\ ABC тупоугольный (рис. 15),
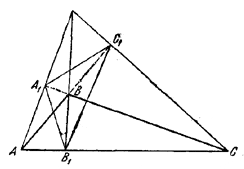
Рис.15.
то вместо (1) будем иметь:
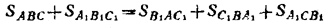
и, соответственно, вместо (2)
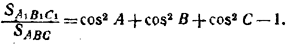 (3) (3)
Наконец, если /\ ABC прямоугольный, то 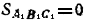 , что, как легко проверить, получается также из формул (2) или (3). , что, как легко проверить, получается также из формул (2) или (3).
________________________________________________
9. 1) Пусть ВО и СО — биссектрисы внутренних углов /\ ABC (рис. 16).
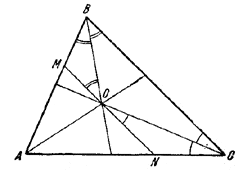
Рис.16.
Легко видеть, что треугольники ВОМ и CON равнобедренные.
Следовательно, MN= BM + CN.
2) Зависимость MN = BM + CN имеет место и в случае внешних биссектрис.
3) Если одна из биссектрис внутренняя, а другая—внешняя (рис. 17), то из внутренних треугольников ВМО и CNO находим MN = CN — BM, когда CN > ВМ,
и MN = BM — СN, когда CN < ВМ.
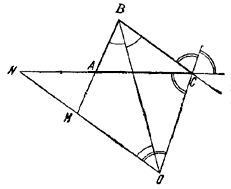
Рис.17.
Итак, в этом случае
MN = | CN — BM |.
Точки М и N совпадают только в случае (3), если /\ ABC равнобедренный (АВ = АС).
________________________________________________
10. Проведем через точку Р три прямые, параллельные сторонам треугольника (рис. 18).
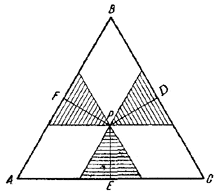
Рис.18.
Три образовавшихся треугольника (заштрихованные на рисунке) также правильные, и сумма их сторон равна стороне АВ = а треугольника ABC. Значит и сумма их высот равна высоте /\ ABC, так что
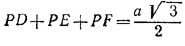
Сумма BD + CE + AF равна сумме сторон заштрихованных треугольников, сложенной с суммой половин этих же сторон, так что
BD + CE + AF = 3/2 а.
Следовательно,
PD + PE + PF = 1
BD + CE + AF √3
________________________________________________
11. Пусть О — точка пересечения медиан в /\ ABC (рис. 19).
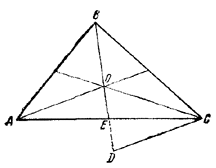
Pис. 19.
На продолжении медианы BE отложим ED = OE. По свойству медиан стороны /\ CDO равны 2/3 сторон треугольника, составленного из медиан. Обозначив площадь последнего через S1 будем иметь:
S1 = 9/4 SCDO
С другой стороны, /\ CDO составлен из двух, а /\ ABC— из шести треугольников, равновеликих /\ СЕО. Поэтому SCDO = 1/3 SABC Следовательно,
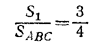
________________________________________________
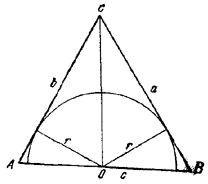
12. Пусть ABC — данный треугольник (рис. 20).
Pис. 20.
Площадь /\ СОВ равна 1/2 аr, а площадь /\ СОА равна 1/2 br. Складывая эти величины и выражая площадь /\ ABC по формуле Герона, получим:
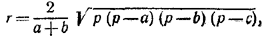
где р = 1/2 (а + b + с).
________________________________________________
13. Пусть R — радиус описанного круга и r —радиус вписанного.
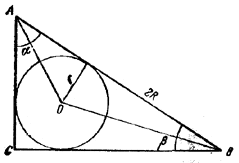
Рис.21.
Тогда (рис. 21) AB = 2R, а также
AB = r ctg α/2 + r ctg β/2.
Отсюда
ctg α/2 + ctg β/2 = 2R/r = 5
Кроме того, α/2 + β/2 = π/4 и ctg (α/2 + β/2) = 1 , т.е.
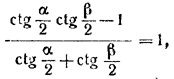
откуда
ctg α/2 ctg β/2 = 6.
Следовательно, ctg α/2 и ctg β/2 равны корням квадратного уравнения
х2— 5х + 6 = 0.
Окончательно получаем:
α = 2arctg 1/2 , β = 2arctg 1/3
________________________________________________
14. Обозначим через а и b стороны данного прямоугольника и через φ — угол между стороной описанного и данного прямоугольников (рис. 22).
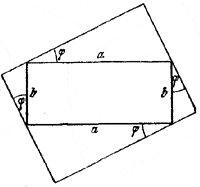
Рис.22.
Тогда стороны описанного прямоугольника будут равны
a cos φ + b sin φ и a sin φ + b cos φ.
По условию задачи
(a cos φ + b sin φ) (a sin φ + b cos φ) = m2,
откуда найдем:
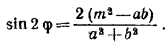
Условием разрешимости задачи будет 0 < sin 2φ < 1, что равносильно следующим неравенствам:
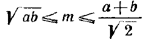
________________________________________________
15. Если /_ AED = /_DEC (рис. 23), то также /_CD£ = = /_DEC, откуда CE = CD.
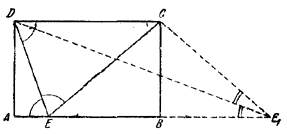
Рис.23.
Следовательно, Е есть точка пересечения стороны АВ с окружностью, описанной из центра С радиусом CD. Задача разрешима, если АВ > ВС, причем имеет два решения, когда АВ > ВС, и одно решение, когда АВ = ВС. (Точка E1 на рис. 23 соответствует второму решению).
________________________________________________
16. Боковая сторона видна из вершины нижнего основания под углом α/2 (рис. 24),
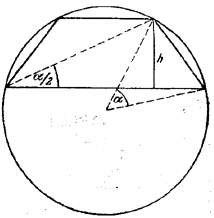
Рис.24.
а средняя линия равна отрезку от этой вершины до основания высоты, опущенной из противоположной вершины, т. е. h ctg α/2 .
Следовательно, площадь трапеции
S = h2 ctg α/2.
________________________________________________
17. Середины диагоналей Е и F трапеции лежат на ее средней линии MN (рис. 25).
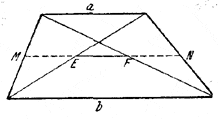
Рис.25.
Но ME = FN = a/2. Следовательно,
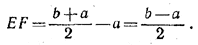
________________________________________________
18. Параллелограмм составлен из 8 треугольников, равновеликих треугольнику АОE. Фигура (восьмиугольник), полученная путем указанного построения, также составлена из 8 треугольников, равновеликих /\ POQ (рис. 26).
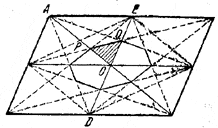
Рис.26.
Так как ОР = 1/3 ОА (по свойству медиан в /\ DAE) и OQ = 1/2 ОE, то
SPOQ = 1/6 SAOE
Следовательно, искомое отношение равно 1/6.
________________________________________________
19. Очевидно, что KLMN — параллелограмм (рис. 27), причем
KL= 2/5 AQ.
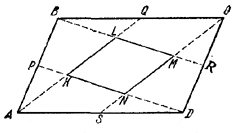
Рис.27.
Следовательно,
SKLMN = SAQCS = 2/5 • 1/2 a2 = 1/5 a2
________________________________________________
|