|
130. Если A—вершина прямого угла в /\ AВС, а С и В лежат на заданных параллельных прямых l1 и l2 (рис. 135),
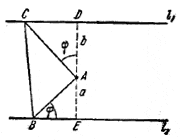
Pис. 135
то
Следовательно, площадь треугольника ABC равна
Отсюда следует, что SABC примет наименьшее значение, равное аb при φ = π/4.
______________________________________________
131. Если R - радиус описанной, а r - радиус вписанной окружности ( рис. 136),
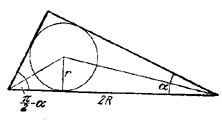
Рис. 136
то
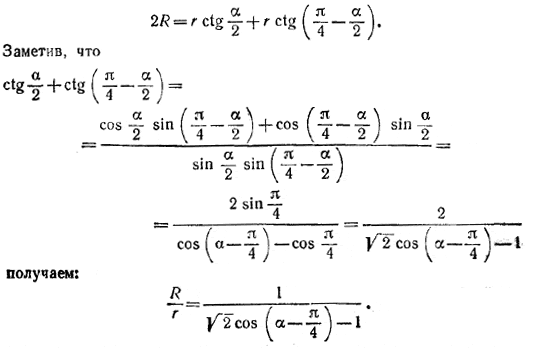
Величина R/r имеет наименьшее значение, когда cos ( α — π/4 ) = 1, т. е. (в силу ограничения 0 < α < π/2 ) когда α = π/4; в этом случае
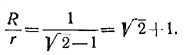
______________________________________________
132. Пусть от прямоугольника ABCD отсечен треугольник с вершиной С так, что получился пятиугольник ABEFD (рис. 137).
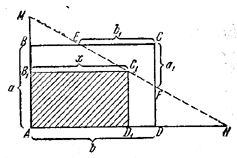
Pис. 137
Ясно, что искомый прямоугольник AB1C1D1 должен иметь вершину C1 на отрезке EF. Задача состоит в том, чтобы найти положение этой вершины.
Чтобы найти точку С1 , продолжим стороны АВ и AD прямоугольника до пересечения с продолжением отрезка EF, образовав треугольник AMN. Пусть
АМ = т, AN = n
и
B1C1 = AD1 = x.
Из подобия треугольников AMN и D1C1N имеем:
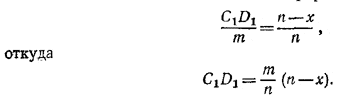
Следовательно, для площади S прямоугольника AB1C1D1 равной AD1•C1D1, получаем выражение
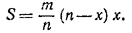
Преобразовав это выражение к виду
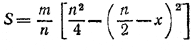 (1) (1)
заключаем, что наибольшее значение S будет иметь тогда, когда n/2 — х = 0, т. е. при х = n/2. Обозначим через С0 положение вершины С1 соответствующее х = n/2.
Заметив, что выражение (1) для S убывает с возрастанием | n/2 — х |, т. е. при движении точки С1 от точки С0 к вершине М или к вершине F, находим, что возможны следующие три случая:
1) Точка С0 лежит на отрезке EF; тогда вершина С1 искомого прямоугольника совпадает с С0.
2) Точка С0 лежит на отрезке ME; тогда С1 надо взять совпадающей с E.
3) Точка С0 лежит на отрезке FN; тогда С1 надо взять совпадающей с F.
Остается найти критерий для различения этих случаев с помощью данных в условии задачи величин а, а1 b, b1
Сначала найдем величину n. Из подобия треугольников ECF и NDF имеем:
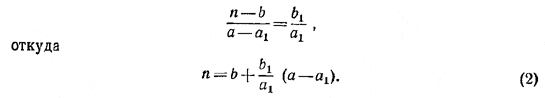
Теперь заметим, что точка С0 попадет внутрь отрезка EF, если выполняются неравенства
b — b1 < х < b.
Подставив сюда х = n/2 с известным значением п, получим:
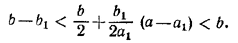
Эти неравенства нетрудно преобразовать к виду

При нарушении левого неравенства точка С0 попадает на отрезок ME, а правого—на FN.
Окончательно получаем следующий результат: если для данных а, b, а1 , b1 выполнены оба неравенства (3), то вершина С1 прямоугольника наибольшей площади лежит внутри отрезка EF, а сторона х этого прямоугольника вычисляется по формуле
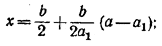
если нарушается левое неравенство (3), то вершина С1 совпадает с точкой Е, а если правое, — то с точкой F.
______________________________________________
133. Проведем окружность, проходящую через точки А и В и касающуюся второй стороны угла (рис. 138).
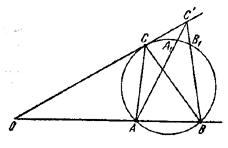
Pис. 138
Точка касания и будет искомой, так как для любой точки С на этой прямой угол АСВ измеряется полуразностью дуг АВ и A1B1, тогда как / АСВ измеряется половиной дуги АВ.
Заметим далее, что (ОС)2 = ОВ•ОА. Следовательно, задача свелась к известному построению среднего геометрического длин двух данных отрезков ОА и ОВ.
______________________________________________
134. Рассмотрим три возможных случая расположения отрезка А В относительно l.
а) АВ | | l. Для любой точки М прямой l имеем | АМ—ВМ | > 0, причем существует точка M0, для которой | АМ0 — ВМ0 | = 0. Эта точка является основанием перпендикуляра, опущенного из середины отрезка АВ на l.
Точки М, для которой величина | AM — ВМ | имела бы наибольшее значение, не существует. Это следует из того, что | AM — ВМ | < АВ и равенство возможно лишь в случае, когда А, В и М лежат на одной прямой.
б) AВ _|_ l. Так как | AM — ВМ | < АВ, то для точки пересечения прямой l с прямой АВ величина | AM — ВМ | примет наибольшее значение, равное длине АВ. Точки М, для которой величина | AM — ВМ | была бы наименьшей, не существует.
в) Прямая АВ не параллельна и не перпендикулярна к l. Ясно, что | AM—ВМ | примет наименьшее значение, если М есть точка пересечения l с перпендикуляром к отрезку АВ в его середине. Наибольшее значение | AM—ВМ | примет тогда, когда точка М будет точкой пересечения АВ с l.
______________________________________________
135. Пусть MN — какое-нибудь положение секущей, AP | | ON и AQ | | ОМ (рис. 139).
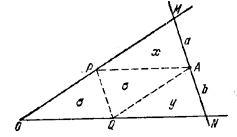
Pис. 139
Введем следующие обозначения:
х = площадь /\ АРМ,
y = площадь /\ AQN,
б = площадь /\ APQ,
S= площадь /\ OMN,
а = АМ, b = AN.
Имеем:
S = 2б + х + у.
Ясно, что
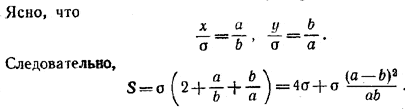
Наименьшее значение S = 4б получается при а = b, что и требовалось доказать.
______________________________________________
136. Пусть a + b = q (рис. 140).
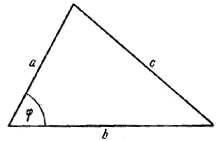
Pис. 140
По теореме косинусов
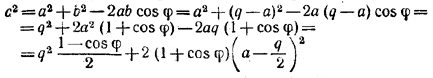
Так как q и φ неизменны, то наименьшее значение с будет при
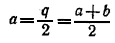 , т. е. при а = b. , т. е. при а = b.
______________________________________________
137. Первое решение. Рассмотрим /\ АВС с основанием АС и обозначим через а, b, с длины сторон, противолежащих соответственно углам А, В, С; положим а+b+ с = р.
Из соотношений
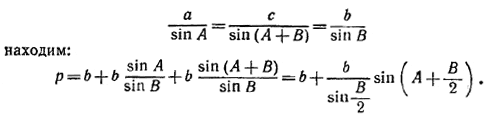
Так как b > 0 и sin B/2 > 0, то р примет наибольшее значение при
А + B/2 = π/2
В этом случае A = С и /\ ABC равнобедренный.
Второе решение. Построим на данном основании АВ сегмент, вмещающий данный угол φ (рис. 141),
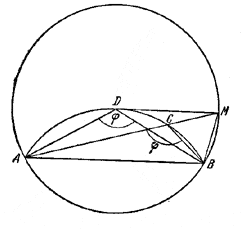
Pис. 141
и рассмотрим два треугольника, вписанных в этот сегмент: равнобедренный /\ ADB, неравнобедренный /\ АСВ. Из точки D радиусом AD = DB опишем окружность, продолжим АС до пересечения с окружностью в точке М и соединим М с D и В. Получим:
AD + DB = AD + DM > АМ = АС + СМ.
Но в /\ ВСМ
/ СВМ = / АСВ — / СМВ = / СМВ,
так как / АСВ = / ADB и измеряется дугой АВ, а / АМВ измеряется половиной дуги АВ. Следовательно, СМ = СВ и AD + DB > АС + СВ
______________________________________________
138. Обозначим через R1 и R2 радиусы окружностей, описанных соответственно около /\ ACD и /\ BCD, а также положим / ADC = φ, AC = b, BC = a (рис. 142).
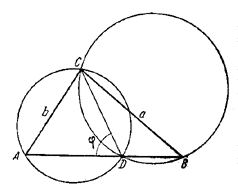
Pис. 142
Имеем:
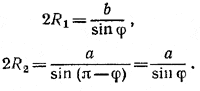
Отсюда 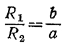 . Радиусы R1 и R2 будут наименьшими тогда, когда φ = π/2; в этом случае D — основание высоты CD. . Радиусы R1 и R2 будут наименьшими тогда, когда φ = π/2; в этом случае D — основание высоты CD.
______________________________________________
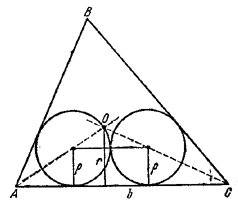
139. Каждый из вырезаемых кругов должен касаться двух сторон /\ AВС (рис. 143);
Pис. 143
кроме того, круги должны касаться друг друга. В противном случае радиус можно увеличить. Поэтому центры кругов лежат на двух биссектрисах внутренних углов, например, АО и СО, где О—центр вписанной в /\ AВС окружности. Если r — радиус вписанного в /\ AВС круга и ρ — радиус вырезанных кругов, то из /\ АОС имеем
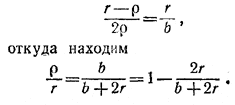
Из этой формулы следует, что ρ будет наибольшим, когда в качестве b взята наибольшая сторона.
______________________________________________
|