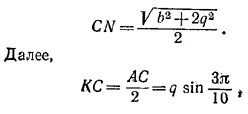|
|
|
|
|
ГЛАВА 6 СТЕРЕОМЕТРИЯ ЗАДАЧИ НА ВЫЧИСЛЕНИЕ Ответы и решения |
|
140. Пусть а — сторона основания, d — диагональ боковой грани призмы, l — боковое ребро (рис. 144).
рис. 144 Имеем:
Из /\ А1ВС1 следует, что 1/2 a = d sin α/2 . Поэтому
и, следовательно,
______________________________________________ 141. Пусть Н — высота пирамиды, а — длина стороны основания.
рис. 145 Рассматривая подобные треугольники OMS и ABS (рис. 145), найдем:
Аналогично из треугольников OKS и CBS получим:
Разделив почленно равенство (1) на (2), будем иметь:
откуда
Подставив это выражение в (1), легко найдем:
В итоге для объема V получаем выражение
______________________________________________ 142. Пусть Н — высота пирамиды, х — высота боковой грани, проведенная из вершины пирамиды, R — радиус круга, вписанного в основание, r —радиус круга, описанного около основания, а — сторона основания.
рис. 146 Из подобия треугольников СА1В1 и CAB (рис. 146) получаем:
Но из /\ ADB имеем Так как, далее, для площади основания и объема имеем следующие формулы:
Подставляя сюда найденное выражение для H, находим:
Так как, далее, х = √ R2 + H2 и a/2 = r sin π/n , то боковая поверхность равна n 1/2 xa = nr sin π/n√ R2 + H2 или окончательно
______________________________________________ 143. Пусть М и N—середины ребер ES и DS (рис. 147);
рис. 147 легко видеть, что AMNC—трапеция, ибо MN | | ED, a ED | | AC. Очевидно также, что MN = 1/2 q Используя формулу (1) для квадрата ¦ медианы треугольника в решении задачи 79, найдем:
ибо / АВК = 3π/10. Если KL—отрезок, соединяющий середины оснований трапеции ACNM, то ( мы воспользовались здесь тем, что Sсеч. = 1/2 (MN + AC) KL = q/16 (2 + √5) √4b2 +3q2 ______________________________________________ 144. Пусть E и F—середины ребер правильной треугольной пирамиды SABC, D — середина отрезка EF (рис. 148).
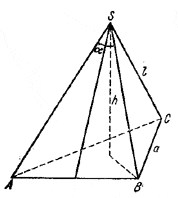
рис. 148 Так как сечение перпендикулярно грани CSA, то / SDB—прямой. Продолжив SD до пересечения с прямой АС в точке М, рассмотрим треугольник MBS. Точка D, очевидно, делит отрезок SM пополам. Так как, кроме того, BD_|_MS, то треугольник МBS равнобедренный; SB = MB. Пусть сторона основания пирамиды равна а. Тогда
Высота боковой грани
______________________________________________ 145. Пусть а — длина стороны квадрата, лежащего в основании призмы, l — длина бокового ребра призмы, d — диагональ боковой грани (рис. 149).
рис. 149 Обозначим через Sсеч. площадь сечения; легко видеть, что полная поверхность призмы равна 4 (S — Sсеч.); поэтому достаточно определить Sсеч.. Имеем:
В итоге после упрощений находим, что полная поверхность призмы равна
______________________________________________ 146. Сторона основания пирамиды равна a = 2r sin α (по известной лемме к теореме синусов).
рис. 150 Боковое ребро (рис. 150)
Поэтому высота пирамиды равна
и следовательно, объем пирамиды равен
______________________________________________ 147. Пусть ABC'D'—указанное сечение пирамиды OABCD. Через вершину О пирамиды и середину ее ребер АВ и CD проведем вспомогательную плоскость OPN (рис. 151).
рис. 151 Легко видеть, что плоскость OPN перпендикулярна к АВ и CD, а отрезки ОР и ON равны. Применяя теорему синусов к треугольнику ОРМ, находим:
Так как D'C' | | DC, то
Применяя теорему синусов к треугольнику PMN, находим
Теперь получаем искомую площадь сечения ABC'D':
______________________________________________ 148. Пользуясь обозначениями рис. 152, рассмотрим 1/8 часть чердака OSBMN. Она состоит из двух пирамид.
рис. 152 Первая пирамида имеет основание SBM и вершину О; ее объем равен
Вторая пирамида имеет основание BMN и вершину О; ее объем будет Таким образом, объем чердака равен ______________________________________________ 149. Пусть ВМ и СМ — перпендикуляры, опущенные из вершин основания В и С ( рис. 153) на боковое ребро SA.
рис. 153 Образованный ими / ВМС является искомым. Обозначим его через β. Очевидно, sin β/2 = BK/ВM (1) Пусть а—сторона основания пирамиды. Тогда
Из равнобедренного треугольника ASB легко находим его высоту ВМ:
______________________________________________ 150. Проведем плоскость через ребро SA и точку N—основание перпендикуляра AN к отрезку ВС (рис. 154).
рис. 154 Пусть NM—высота треугольника ASN. Отрезок NM, будучи перпендикулярен к AS и ВС, очевидно, равен d. Обозначим через а сторону основания пирамиды. Тогда
______________________________________________ 151. Пусть AD = a, BC = b (рис. 155).
рис. 155 Проведем отрезок EF, соединяющий середины оснований трапеции. Очевидно, что двугранный угол, прилегающий к AD, меньше угла, прилежащего к ВС. Пусть / SEO = α , тогда / SFO = 2α. Имеем; SO = OF • tg 2α = OE • tg α. Но OF = b/2 tg φ/2 ; OE = a/2 tg φ/2 и мы приходим к уравнению a tgα = b tg 2α, решив которое, найдем:
*) Этот результат показывает, что в случае a < 2b задача теряет смысл. Далее, получаем:
и, наконец, объем пирамиды равен
______________________________________________ 152. Пусть SL_|_AB, SK _|_ AC и SM— перпендикуляр к плоскости Р (рис. 156).
рис. 156 По условию SA = 25 см, SL = 7 см и SK = 20 см. По теореме Пифагора легко находим, что АК=15см и AL = 24 см. Продолжим отрезок КМ до пересечения в точке Q со стороной АВ. Легко видеть, что / AQK = 30°, следовательно, AQ = 30 см. Поэтому LQ = 6 см, a LM = 6 tg 30° = 2 √3 см. Из прямоугольного треугольника SML теперь находим, что SM =√72 —(2√3 )2 = √37 см. ______________________________________________ 153. Пусть S — вершина пирамиды, SO—высота, BN = NC (рис. 157).
рис. 157 Обозначим сторону основания пирамиды через а. Временно положим SM/SN= λ. Тогда из подобия треугольников легко находим, что
а из /\ МКO получаем
Площадь сечения равна
Площадь основания, как площадь правильного шестиугольника со стороной а, равна
Следовательно, задача сводится к нахождению λ. Для этой цели положим / SNO = φ . Тогда по теореме синусов из /\ SOM получим:
______________________________________________
|










 , и поэтому
, и поэтому