|
197. Пусть S — полная поверхность конуса, S1—поверхность шара, r1 и r — радиусы верхнего и нижнего оснований конуса, l —длина его образующей. Пусть далее CMDL—трапеция, полученная в осевом сечении конуса, О — центр вписанного шара, AB _|_ LD и OF _|_ MD (рис. 200).
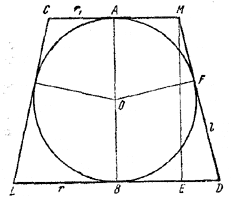
рис. 200
Имеем:
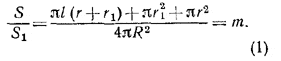
Легко видеть, что AM = MF и BD = FD, так как О — центр вписанного в трапецию круга, поэтому
l = r + r1 (2)
Воспользовавшись этим равенством, из равенства (1) получим:
l2 + r2 + r12 = 4mR2. (3)
Из треугольника MED, далее, следует:
l2 = ( r — r1)2 + 4R2. (4)
Исключая l из равенств (2) и (4), найдем:
r r1 = R2. (5)
С помощью этого равенства, исключив l из (2) и (3), мы получим:
r2 + r12 = R2(2m—1). (6)
Решив теперь систему (5), (6), найдем:
r = R/2 ( √2т + 1 + √2т —3);
r1 = R/2 ( √2т + 1 — √2т —3);
Таким образом, при т < 3/2 задача не имеет решения; при m = 3/2 усеченный конус превращается в цилиндр.
______________________________________________
198. Возможны два случая: 1) вершина конуса и шар лежат по разные стороны от касательной плоскости; 2) вершина конуса и шар лежат по одну сторону от касательной плоскости.
Рассмотрим первый случай. Проведем плоскость через ось конуса и образующую конуса ВС, о которой говорится в условии задачи (рис. 201).
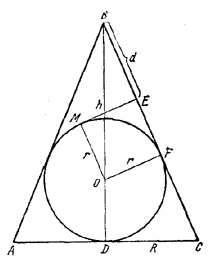
рис. 201
Эта плоскость в сечении с конусом даст треугольник ABC, в сечении с шаром—окружность С центром О; плоскость, перпендикулярная к ВС, будет пересечена по прямой ME (М.—точка касания).
Проведем BD_|_AC и OF _|_ВС Пусть BD = h, OD = OF = r, CD = R. Очевидно, OMEF — квадрат, поэтому
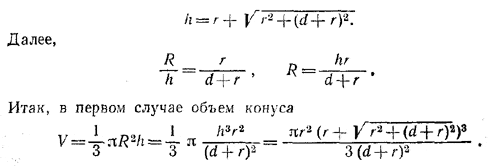
Во втором случае задача решается аналогично. Объем конуса оказывается равным
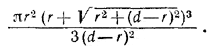
______________________________________________
199. Рассмотрим осевое сечение ABC конуса. Пусть BF — высота в треугольнике ABC, N и М — точки касания круга, вписанного в треугольник ABC, со сторонами АВ и ВС, О — центр круга, Е — точка пересечения меньшей дуги MN с отрезком BF, D — точка пересечения отрезков MN и BF (рис. 202).
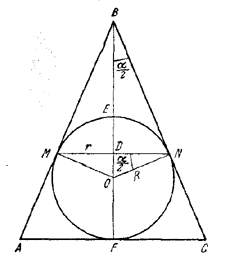
рис. 202
Положим DM = r, DE = H, BD = h. Искомый объем равен
V = 1/3 πr2h — 1/3πH2 (3R — H).
Но
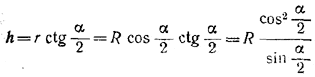
и
H = R — R sin α/2;
следовательно,
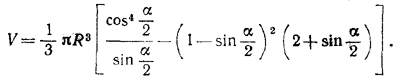
______________________________________________
200. Обозначим через r и r1 радиусы шаров и рассмотрим сечение шаров плоскостью, проходящей через их центры О и О1;
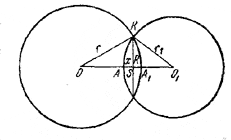
рис. 203
пусть АА1 = 2а, KS = R и AS = x (рис. 203); тогда A1S = 2a — x.
Полная поверхность линзы равна
2xar1 + (2a — x)2ar = S. (1)
Из треугольника OKS имеем
r2 = R2 + [r —(2а — x)]2
или
R2—2r (2а — x) + (2а — x)2 = 0. (2)
Аналогично из треугольника O1KS имеем r1 = R2 + (r1—х)2 или
R2 — 2r1х + x2 = 0. (3)
Из (2) и (3) находим:
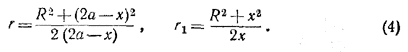
Подставив эти выражения для r и r1 в равенство (1), получим уравнение
π(R2 + х2) + π[R2 + (2а — х)2] = S
или
х2—2ах + R2 + 2а2 — S/2π= 0,
откуда
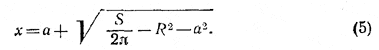
Подставив это значение х в формулы (4), после упрощений получим:
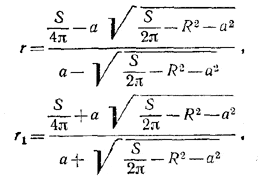
Выбор другого знака перед корнем в (5) сводится к перемене обозначений r и r1.
______________________________________________
201. Пусть V1 и V2 суть соответственно объемы меньшего и большего шаровых сегментов, на которые разбивает шар плоскость, проходящая через линию касания шара с конусом. Пусть, далее, R—радиус шара, h — высота меньшего сегмента, Н — высота конуса, r — радиус его основания (рис. 204).
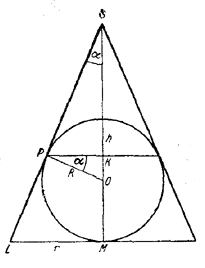
рис. 204
Тогда
V1 = 1/3πh2 (3R— h), V2 = 4/3πR3 — π/3 h2(3R — h).
Задача сводится к нахождению отношения h/R . Обозначив через α угол между осью конуса и образующей, из /\ РKО находим:
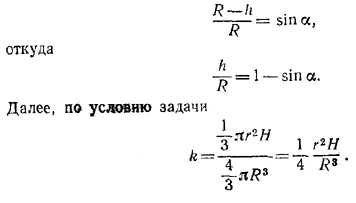
Выразим теперь r и R через R и α. Имеем:
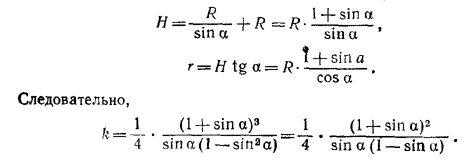
Подставляя сюда sin α = l — h/R, получаем уравнение относительно h/r= z
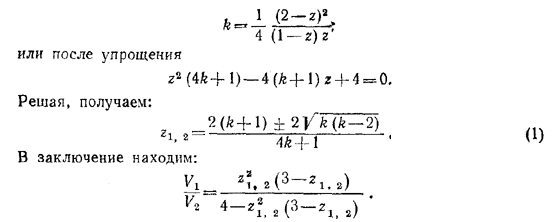
Задача имеет два решения, так как оба корня квадратного уравнения при k > 2 имеют смысл.
______________________________________________
202. Радиус r каждой из восьми вписанных сфер мы найдем, рассмотрев треугольник АОС в плоскости, проходящей через центры этих сфер и центр О сферы S (рис. 205, а).
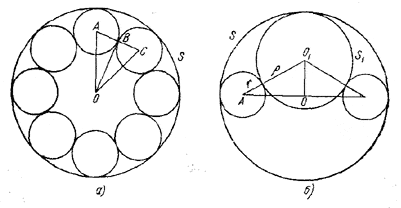
рис. 205
Имеем:
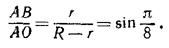
Отсюда
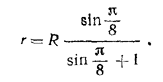
Проведя сечение через центр О сферы S, центр О1 сферы S1 и центры двух противолежащих сфер радиуса r (рис. 205, б), мы получим из прямоугольного треугольника АОО1:
АО12 = AO2 + OO12
или
( r + ρ )2 = ( R — r )2 + ( R — ρ )2
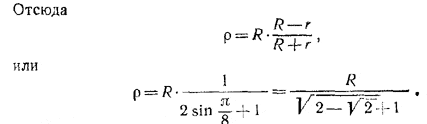
______________________________________________
203. Так как вписанные сферы равны между собой, то их центры одинаково удалены от центра О сферы S. Следовательно, центр симметрии указанного в условии задачи куба совпадает с центром О сферы S (рис. 206).
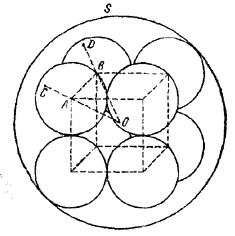
рис. 206
Пусть х — искомый радиус сфер. Легко видеть, что тогда ребро куба будет АВ = 2х, а половина диагонали куба
AO = CO — CA = R — x.
Так как, с другой стороны,
АО = 1/2 • 2х√3 ,
то получаем уравнение R— х = х√3 , откуда
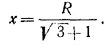
______________________________________________
204. Пусть r — радиус основания каждого из двух вписанных конусов. Их общая часть состоит из двух равных усеченных конусов. Обозначим через r1 и r2 соответственно радиусы верхнего и нижнего оснований усеченного конуса и через Н—его высоту. Искомое отношение объемов равно
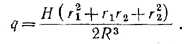
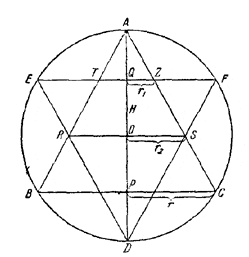
рис. 207
Из подобия треугольников AQZ, AOS, АРС (рис. 207) имеем:
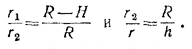
Так как, кроме того, H = h — R и
r = √R2 — H2 = √2Rh2 — h2,
то два предыдущих равенства позволяют выразить r1 и r2 через R и h:
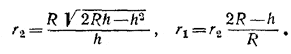
Так как по условию задачи h/R = k, то
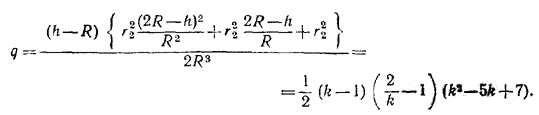
______________________________________________
205. Пусть радиусы круговых сечений с площадями S1 и S2 равны R1 и R2 , а расстояния от центра шара до этих сечений соответственно равны l1 и l2 (l1< l2). Обозначим через R радиус шара, через r — радиус искомого сечения, а через l — расстояние от этого сечения до центра шара.
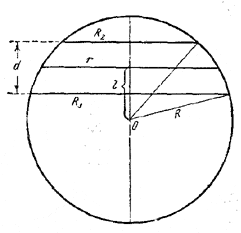
рис. 208
Тогда (рис. 208)
l2 — l1 = d (1)
и l12 + R12 = l22 + R22 = R2
Из этих двух уравнений находим:
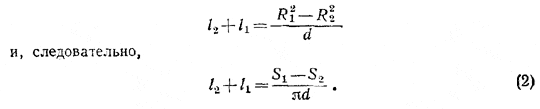
Из уравнений (1) и (2) получаем:
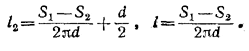
Поэтому искомая площадь равна
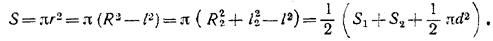
______________________________________________
206. Обозначим через r искомый радиус основания конуса. Рассмотрим фигуру, получающуюся в сечении, проведенном через центр одного из шаров и ось конуса (рис. 209).
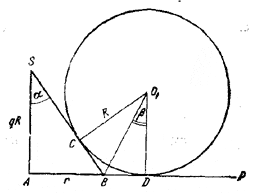
рис. 209
Заметим, что расстояние между центрами двух касающихся шаров равно 2R. Используя легко доказуемый факт, что центр основания конуса А расположен на одинаковом расстоянии от всех трех точек касания сфер с плоскостью Р, находим:
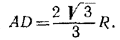
Легко видеть, что / SB A = / СО1О = 2β и, следовательно,
2β = π/2 — α
Взяв тангенсы углов, стоящих в обеих частях этого равенства, получаем:
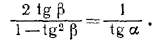 (1) (1)
Из рис. 209 видно, что 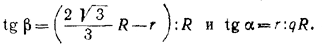
Если теперь положить r/R = х , то равенство (1) приведет нас к следующему уравнению относительно х :
3(q — 2) х2— 4√3 (q — 1) х + q = 0.
Отсюда при q = 2 получаем х = √3/6 , следовательно, r = √3/6 R. Если же q =/= 2, то
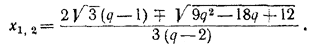
Так как  то в указанной формуле следует взять знак минус. Второй корень при q > 2, как нетрудно показать, больше, чем то в указанной формуле следует взять знак минус. Второй корень при q > 2, как нетрудно показать, больше, чем  , и отвечает конусу, касающемуся сфер извне; при q < 2 второй корень отрицателен. , и отвечает конусу, касающемуся сфер извне; при q < 2 второй корень отрицателен.
______________________________________________
207. Центры четырех первых шаров лежат в вершинах правильного тетраэдра, так как расстояния между центрами любых двух касающихся шаров равны 2R. Нетрудно показать, что центры пятого и шестого шаров совпадают с центром тяжести тетраэдра (рис. 210).
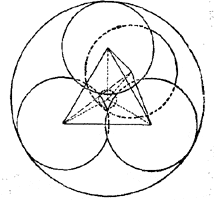
рис. 210
Пусть r — радиус пятого (большего) шара, а ρ — радиус шестого шара. Очевидно,
r = ρ + 2R. (1)
Пользуясь тем, что расстояние от центра тяжести до вершины рассматриваемого тетраэдра равно √6/2 R получаем:
ρ + R = √6/2 R. (2)
Отсюда ρ = R ( √6/2 — 1 ) , а из формулы (1) r = R ( √6/2 + 1 ) .
Таким образом, искомое отношение объемов равно
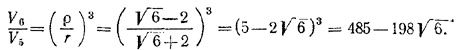
______________________________________________
208. Пусть А, В, С— центры шаров радиуса R, А1, B1, C1 — проекции этих центров на плоскость, О — центр четвертого шара, радиус r которого нужно найти (рис. 211).
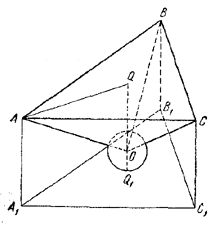
рис. 211
Соединив центры всех шаров, мы получим, очевидно, правильную треугольную пирамиду ОАВС, у которой AB = BC = AC = 2R, АО = ВО = СО = R + r, OQ = R— r. Отрезок AQ есть радиус описанной около /\ ABC окружности, поэтому
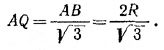
Из треугольника AQO по теореме Пифагора находим:
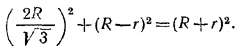
Решив это уравнение, получаем r = R/3.
______________________________________________
209. Пусть А, В, С, D — центры больших шаров. Рассмотрим проекцию всех шаров на плоскость А, В, С, D (рис. 212).
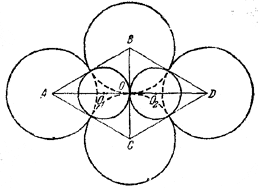
рис. 212
Так как центры малых шаров равноудалены от центров соответствующих больших шаров, они спроектируются в центры тяжести O1 и О2 равносторонних треугольников ABC и BCD. Так как, кроме того, радиусы малых шаров по условию равны, то отрезок, соединяющий их центры, параллелен рассматриваемой плоскости и делится точкой касания шаров пополам. Ввиду этого проекция точки касания окажется на отрезке ВС. Отсюда следует, что малые шары спроектируются в круги, вписанные в треугольники ABC и BCD. Поэтому радиус малых шаров равен
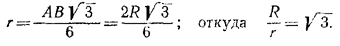
______________________________________________
|