|
233. Пусть Р—одна из плоскостей, проходящих через данную точку A, а М — проекция данной точки В на плоскость Р. Пусть, далее, С — середина отрезка АВ (рис. 238).
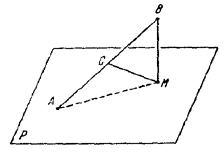
рис. 238
Так как треугольник АМВ прямоугольный, то СM = 1/2 АВ.
Таким образом, все точки М находятся от точки С на одном и том же расстоянии 1/2 АВ и, следовательно, расположены на сфере радиуса 1/2 АВ с центром в точке С. Легко видеть, кроме того, что любая точка указанной сферы совпадает с одной из проекций точки В. Таким образом, искомое геометрическое место есть сфера с диаметром АВ.
______________________________________________
234. Пусть О — центр дадаого шара. Проведем через данную прямую l некоторую плоскость Р, пересекающую сферу по окружности с центром в точке М (рис. 239).
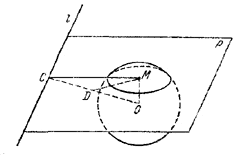
рис. 239
Как известно, ОМ _|_Р. Проведем, далее, через точку О плоскость Р1, перлендакулярную к прямой l. Точку пересечения плоскости Р1 и прямой l обозначим через С. Так как плоскости Р1 и Р перпендикулярны, то отрезок ОМ содержится в плоскости Р1.
Рассмотрим теперь прямоугольный треугольник ОМС. Точка С не зависит от выбора секущей плоскости Р, и гипотенуза ОС прямоугольного треугольника ОМС есть величина постоянная. Если D — середина ОС, то MD = OC/2 . Следовательно, если l не имеет со сферой общих точек, то искомое геометрическое место есть часть дуги окружности радиуса OC/2 , заключенная внутри сферы (дуга лежит в плоскости P1 и проходит через центр сферы). Если l касается сферы, то искомое геометрическое место — окружность радиуса R/2 , где R — радиус сферы. Наконец, если l пересекает сферу, то геометрическое место точек М — окружность радиуса OC/2.
______________________________________________
235. Искомым геометрическим местом является поверхность вращения, которая получается в результате вращения дуги окружности или полной окружности (см. решение предыдущей задачи) вокруг ее диаметра ОС.
______________________________________________
236. Докажем, что искомое геометрическое место есть сфера радиуса R√6/2 и что центр этой сферы совпадает с центром данной сферы.
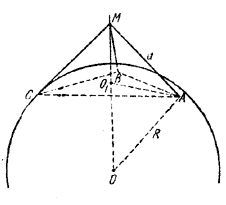
рис. 240
Пусть М — произвольная точка искомого геометрического места; отрезки MA, MB и МС (рис. 240), будучи отрезками касательных, проведенных к сфере из одной общей точки, равны между собой. Поэтому прямоугольные треугольники АМС, СМВ и АМВ равны. Следовательно, /\ ABC равносторонний. Очевидно, что отрезок ОМ пересечет его в центре тяжести О1.
Пусть AM= а, тогда АС = а √2 и АО1 = a√6/3 . Подставляя эти значения в равенствоOM•AO1 = OA•AM (мы пользуемся здесь тем, что /\ ОAM прямоугольный, и записываем двумя способами его площадь), получим:
ОM • a √6/3= Ra
Отсюда
OM = √6/2 R
Таким образом, точка М лежит на указанной выше сфере. Вращая данный шар вместе с касательными AM, СМ и ВМ вокруг центра О, мы убедимся в том, что любая точка сферы принадлежит рассматриваемому геометрическому месту.
______________________________________________
237. Данную точку пространства обозначим через А, точку пересечения прямых—через В, основание перпендикуляра, опущенного из А на плоскость, — через С.
Возьмем, далее, любую прямую, проходящую через точку В, и опустим на нее перпендикуляр AD (рис. 241).
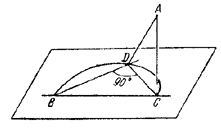
рис. 241
Тогда по известной теореме CD_|_BD.
Следовательно, точка D лежит на окружности, диаметром которой является отрезок ВС. Легко показать, что и, обратно, любая точка указанной окружности есть основание перпендикуляра, опущенного из точки А на некоторую прямую рассматриваемого семейства. Поэтому искомое геометрическое место есть окружность с диаметром ВС.
______________________________________________
238. Возможны два случая.
1) Прямая АВ не параллельна рассматриваемой плоскости Р. Обозначим через D соответствующую точку пересечения АВ и Р (рис. 242).
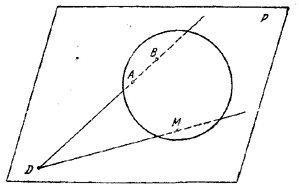
рис. 242
Пусть М — точка касания плоскости с одной из сфер рассматриваемой совокупности. Через прямые АВ и DM проведем плоскость. Последняя пересечет сферу по окружности, касающейся прямой DM в точке М. По известному свойству касательной и секущей, проведенных из одной точки к окружности, имеем: DB•DA = DM2. Следовательно, отрезок DM имеет постоянную длину √DB•DA, не зависящую от выбора сферы, и, значит, все точки М лежат на окружности радиуса r = √DB•DA с центром в точке D. Обозначим эту окружность через С. Пусть теперь, наоборот, М есть некоторая точка окружности С; докажем, что она принадлежит рассматриваемому геометрическому месту.
Проведем через точки А, В и М вспомогательную окружность и центр ее обозначим через О1 (рис. 243).
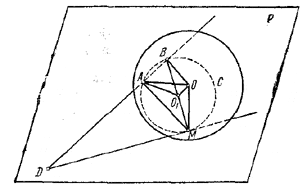
рис. 243
Так как в наших условиях DB•DA = DM2, то прямая DM является касательной к этойокружности и, следовательно, О1М_|_DM. Восставим теперь в точке М перпендикуляр к плоскости Р, а в точке О1 —перпендикуляр к плоскости вспомогательной окружности. Эти два перпендикуляра лежат в плоскости, перпендикулярной к прямой DM в точке М и не параллельны (в противном случае точка O1 , а вместе с ней и точки А и В оказались бы в плоскости Р). Поэтому эти перпендикуляры пересекаются в некоторой точке О. Легко видеть, что О А = OВ = OМ, ибо проекции этих отрезков О1А, О1В и О1М равны между собой как радиусы окружности. Поэтому если построить сферу с центром в точке О и радиусом ОМ, то она коснется плоскости Р и пройдет через точки А и В. Таким образом, обратно, любая точка окружности С принадлежит нашему геометрическому месту. Следовательно, искомое геометрическое место есть окружность С.
2) В случае, когда прямая АВ параллельна плоскости, искомое геометрическое место представляет собой прямую, которая лежит в плоскости Р, перпендикулярна к проекции отрезка АВ на плоскость Р и делит ее пополам.
______________________________________________
239. Случай а). Пусть D — середина отрезка АВ (рис. 244), С — подвижная точка, Q — центр тяжести /\ AВС, Q'—центр тяжести /\ ASB. Так как точка Q делит отрезок DC в отношении 1:2, то геометрическое место этих точек есть, очевидно, луч, параллельный ребру SE и проходящий через точку Q'—центр тяжести /\ ASВ.
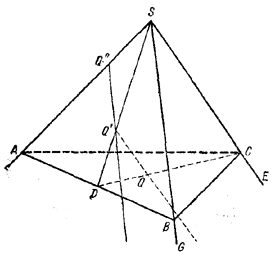
рис. 244
Случай б). Если теперь и точка В перемещается по ребру SG, то центры тяжести Q' треугольников ASB расположатся на луче, параллельном ребру SG и проходящем через точку Q", которая делит отрезок AS в отношении 2:1, считая от А к S, а соответствующие каждому фиксированному положению точки В лучи, рассмотренные в случае а), заполнят сечение трехгранного угла плоскостью, проходящей через точку Q" параллельно ребрам SG и SE.
______________________________________________
|