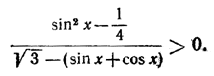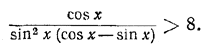ГЛАВА   4

ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ  ФУНКЦИИ

241.   Решить неравенство sin x > cos² x.    Решение

242.   При каких х выполняется неравенство

4 sin² x + 3 tg x — 2 sec² x  > 0?    Решение

243. Решить неравенство

sin x sin 2x  < sin 3х sin 4х,       если 0 < х < ^π/₂.  Решение

244. Решить неравенство

  Решение

245.  Найти все значения х, большие нуля, но меньшие 2π, для которых выполняется неравенство

cos x — sin x — cos 2x > 0.   Решение

246. Решить неравенство

  Решение

247.  Решить неравенство

cos³ x cos 3x — sin³ x sin 3x  > ⁵/₈ .    Решение

248.  Доказать при 0  <  φ <  ^π/₂ неравенство

ctg ^φ/₂ > l + ctg φ.    Решение

249. Доказать справедливость неравенства

(1 —  tg² x) (1 — 3 tg² x) (1 + tg 2x tg 3x) > 0

для всех значений х, при которых левая часть имеет смысл.  Решение

250.  Доказать справедливость неравенства

(ctg² x — 1) (3 ctg² x — 1) (ctg 3x tg 2x — 1 )  < — 1

для всех значений х, при которых левая часть имеет смысл. Решение

251.  Полагая tg θ = n tg φ    (n  > 0), доказать, что

   Решение

252.  Доказать неравенство

При каких значениях х достигается равенство?   Решение

253. Доказать, что при 0  <  φ <  ^π/₂  выполняется неравенство

cos sin φ > sin соs φ.   Решение

254. Пусть n — целое положительное число, большее 1, и угол α удовлетворяет   неравенству    Показать, пользуясь методом полной индукции, что тогда

tg nα > п tg α.    Решение

255.  Пусть 0 < α₁  < α₂  < . . . < α_n  <  ^π/₂.    Доказать, что тогда

 Решение

256. Доказать, что если А, В, С—углы треугольника, то

  Решение

257. Доказать, что при 0 < х < ^π/₄   справедливо неравенство

  Решение