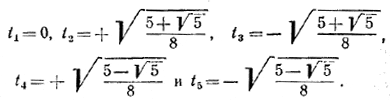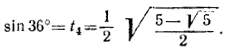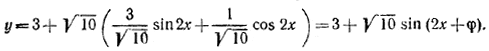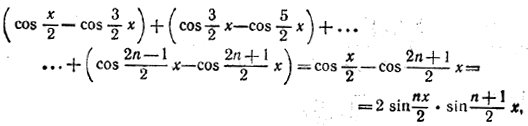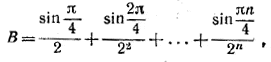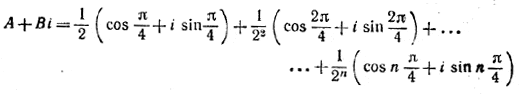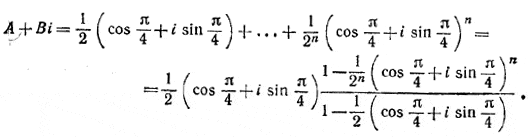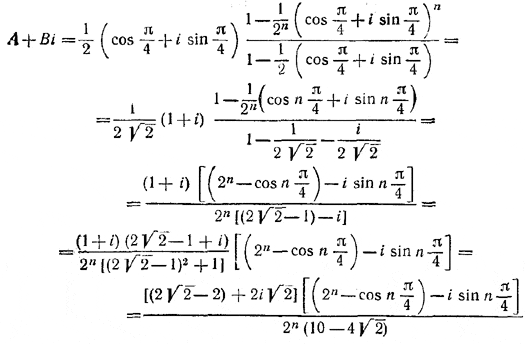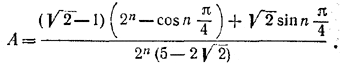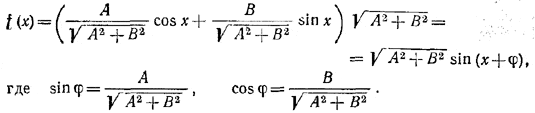|
|
|
|
|
ГЛАВА 6 РАЗНЫЕ ЗАДАЧИ Ответы и решения |
|
258. Положим arctg 1/5 = α, arctg 5/12 = β и рассмотрим tg (2α — β ). Пользуясь формулой для тангенса разности двух углов, получаем: Но так как tg α = 1/5 , то sin (2α — β) = sin ( 2 arctg 1/5 — arctg 5/12 ) = 0. ________________________________________________ 259. Покажем, что tg (α + 2β ) = l. Для нахождения tg (α + 2β ) применим формулу
Предварительно вычислим tg 2β по формуле
Нужно найти cos β и cos 2β. Но cos β = + √1 — sin2 β = 3/√10 (так как β — угол первой четверти), а cos 2β = cos2β — sin2 β = 4/5. Следовательно, tg 2β = 3/4. Подставив найденное значение tg 2β в (1), получим tg (α + 2β ) = l Докажем теперь, что α + 2β = π/4. Так как Отсюда находим, что 0 < α + 2β < 3/4 π. Но единственный угол, заключенный между 0 и 3/4 π, тангенс которого равен 1, есть угол π/4. Итак, α + 2β = π/4. ________________________________________________ 260. Необходимо, чтобы cos х =/= 0, sin х =/= 0, sin х =/= — 1, откуда х =/= kπ/2 (k—целое). При всех значениях х, кроме х =kπ/2, у имеет смысл и Из (1) следует, что у > 0, так как при х =/= kπ/2 cos х < 1 и sin х < 1. ________________________________________________ 261. Преобразуя произведение sin α • sin 3α в сумму, по формуле (13) , получим sin α • sin 3α = 1/2 sin 2α (cos 2α — cos 4α) = 1/4 sin 4α —1/2 sin 2α • cos 4α <1/4 + 1/2 < 4/5 ________________________________________________ 262. Так как sin 5х = sin 3х cos 2х + cos 3х sin 2х, тo используя формулы (5) — (8) , найдем после несложных вычислений sin5x = 5sin x —20 sin3 x + 16 sin5 x. (1) Полагая в формуле (1) х = 36°, получим уравнение 16t5 —20t3 + 5t = 0 для определения sin 36°. Это уравнение имеет следующие корни
Из них положительными являются корни t2 и t4 Но sin 36° =/= t2, ибо
________________________________________________ 263. Используя тождество, доказанное в задаче 50, получим , ________________________________________________ 264. В результате простых преобразований получаем y = l — cos 2x + 2( l + cos 2x) + 3sin 2x = 3 + 3sin 2x + cos 2x. Вводя вспомогательный угол φ = arctg 1/3, будем иметь
Следовательно, наибольшее значение у равно 3 + √10, а наименьшее равно 3 — √10. ________________________________________________ 265. Если п — целое число, удовлетворяющее условию задачи, то при всех х имеем: cos п (х + 3π) • sin 5/n (х + 3π) = cos nx • sin 5/n х. (1) Полагая, в частности, х = 0, мы из (1) заключаем, что п должно удовлетворять уравнению sin 15π/n = 0. Этому уравнению удовлетворяют только те целые числа, которые являются делителями числа 15. n = ±1, ±3, ±5, ±15. (2) Непосредственной проверкой убеждаемся в том, что при каждом из этих значений функция cos nx • sin 5/n х имеет период 3π. Формулой (2) исчерпываются все искомые значения n. ________________________________________________ 266. Так как исследуемая сумма равна нулю при х = x1, то а1 cos (α1 + х1) + ... + аn cos (αn + x1) = = (а1 cos α1+ ... + аn cos αn) cos х1 — (а1 sin α1 + ... + аn sin αn) sin х1= 0. (1) Но по условию задачи а1 cos (α1 + х1) + ... + аn cos (αn + x1) = 0. (2) Кроме того, sin х1 =/= 0, так как х1 =/= kπ. Из (1) и (2) получаем а1 sin α1 + ... + аn sin αn = 0. (3) Пусть теперь х —любое число. Тогда а1 cos (α1 + х) + ... + аn cos (αn + x) = = (а1 cos α1+ ... + аn cos αn) cos х — (а1 sin α1 + ... + аn sin αn) sin х = 0. так как в силу (2) и (3) суммы, стоящие в скобках, равны нулю. ________________________________________________ 267. Предположим противное, т. е. допустим, что существует Т =/= 0 такое, что при всех х > 0 будет cos √x +T = cos √x (1) (ограничение х > 0 необходимо потому, что при х < 0 радикал √x будет мнимым). Положим сначала в формуле (1) х = 0; тогда cos √T = cos 0 =1 (2) и, стало быть, √T = 2kπ. (3) Затем подставим в (1) значение х = Т. Тогда, очевидно, будем иметь согласно (1) и (2): cos √2T = cos √T = 1, откуда cos √2T = 2lπ Так как по предположению Т =/= 0, то, разделив (4) на (3), получим √2 = l/k , где l и k —целые числа. Последнее, как известно, невозможно. ________________________________________________ 268. Первое решение. Рассмотрим сумму S = (cos x + i sin x) + (cos 2x + i sin 2x) + ... + (cos nx + i sin nx) и, пользуясь формулой Муавра, (cos x + i sin x)n = cos nx + i sin nx , вычислим S как сумму геометрической прогрессии. Получим
Сумма sin x + sin 2x + ...+ sin nx равна мнимой части S. Второе решение. Умножив левую часть на 2 sin x/2 и при менив формулу (13) , получим
откуда и следует нужная формула. ________________________________________________ 269. Обозначим искомую сумму через А и прибавим к ней вторую сумму
умножив ее предварительно на i. Получим
Применив формулу Муавра, находим
В последнем выражении использована формула для суммы членов геометрической прогрессии. Искомая сумма А может быть найдена как вещественная часть полученного выражения. Заметив, что cos π/4 = sin π/4 — 1/√2 последовательно находим
Выделяя вещественную часть, получаем
________________________________________________ 270. Утверждение будет доказано, если мы установим, что A = В = 0. Пусть A2 + В2 =/= 0, т. е. по крайней мере одно из чисел А, В отлично от нуля. Тогда
Пусть теперь x1 и x2—два указанных в задаче значения аргумента; тогда f (x1) = f (x2) = 0, и так как √A2 + B2 =/= 0, то sin ( x1 + φ )= sin ( x2 + φ ) = 0. Отсюда x1 + φ = mπ, x2 + φ = nπ и, следовательно, x1—x2 = kπ при некотором целом k. Это равенство приводит к противоречию, так как по условию x1—x2 =/= kπ. Следовательно, A2 + В2 = 0, откуда А = В = 0. ________________________________________________ |
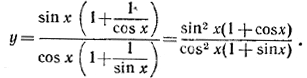(1)
Подставляя tg 2α и tg β в формулу (1), находим tg (2α — β) = 0. Тогда
(1)
и, кроме того, по условию задачи α и β — углы первой четверти, то 0 < α < π/4 и 0 < β < < π/4. 
(1)
и, следовательно, t2 > 1/√
, откуда следует, что наибольшее значение φ (х) равно 1, а наименьшее 1/4.
