ИЗМЕНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.

Изменение функций sin φ и cos φ
Изменение функций tg φ и ctg φ

Изменение функций sin φ и cos φ

Используя тригонометрический круг, выясним, как с изменением аргумента φ изменяются функции sin φ и cos φ.

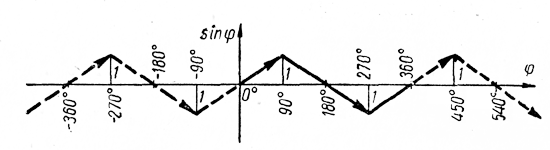
Изменение функции sin φ

Пусть угол φ непрерывно возрастает от 0° до 90°. Тогда ордината соответствующего вектора  будет непрерывно возрастать от 0 до 1. Следовательно, при увеличении угла от 0° до 90° синус его возрастает от 0 до 1.

Если угол φ непрерывно возрастает от 90° до 180°, то ордината соответствующего вектора будет непрерывно уменьшаться от 1 до 0. Следовательно, при увеличении угла φ от 90° до 180° синус его уменьшается от 1 до 0.

Точно так же можно установить, что при возрастании угла φ от 180° до 270° синус его уменьшается от 0 до —1 , а при возрастании угла φ от 270° до 360° синус его увеличивается от —1 до 0 .

Если угол φ оканчивается в 1-й или во 2-й четверти , то ордината соответствующего вектора положительна. Поэтому синусы углов, оканчивающихся в 1-й и во 2-й четвертях, положительны.

Если же угол φ оканчивается в 3-й или в 4-й четверти , то ордината соответствующего вектора отрицательна. Поэтому и синусы этих углов отрицательны.

Схематично поведение функции sin φ при изменении угла φ в интервале от 0° до 360° представлено сплошной линией . Пунктирная линия схематично показывает изменение функции sin φ в других интервалах. Она получена посредством периодического   продолжения  сплошной  линии   влево  и   вправо.

Из отмеченных выше свойств следует особо подчеркнуть следующее Свойство острых углов: чем больше острый угол, тем больше его синус. Так, sin 55° > sin 54°; sin 13° 56' >  sin 13°54' и т. д.

Это утверждение, верное для острых углов, не распространяется на произвольные углы. Например, угол в 180° больше угла в 0°. Однако sin 180° = sin 0° = 0.

Аналогично тому, как мы изучили функцию sin φ, может быть рассмотрена и функция cos φ.

Изменение функции cos φ

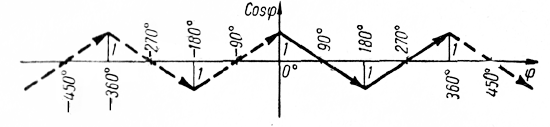
При увеличении угла от 0° до 90° косинус  его уменьшается от 1 до 0; при увеличении угла от 90° до 180° косинус его уменьшается от 0 до —1; при увеличении угла  от  180° до 270°  косинус его увеличивается от —1 до 0;    при   увеличении    угла   от 270° до 360° косинус его увеличивается от 0 до 1.

Косинусы углов, оканчивающихся в 1-й или в 4-й четвертях, положительны; косинусы углов, оканчивающихся во 2-й или в 3-й четвертях, отрицательны.

Схематично поведение функции у = cos x при изменении аргумента φ в интервале от 0° до 360° представлено сплошной линией . Пунктирная линия схематично показывает изменение φ функции cos φ в других интервалах. Такая картина обусловлена периодичностью косинуса.

Следует особо подчеркнуть следующее свойство косинусов острых углов: чем больше острый угол, тем меньше его косинус. Так, cos 55° < cos 54°; cos 13° 56'<cos 13°54' и т. д.

Это утверждение, верное для острых углов, не распространяется на произвольные углы. Например, угол в 270° больше угла в 180°. Вместе с тем cos 270° > cos 180° (0 > —1).

Упражнения

1. Определить    знаки   следующих   выражений:

1)  sin  153°;           4) sin  (—402°);       7) cos (— 1230°);

2)  sin  273°;           5) cos  73°;               8) cos 140°;

3)  sin   301°;           6) sin   910°;             9) sin 1000° · cos 1000°.

2.  Доказать неравенства:

1)  sin 61° > sin 60°;                              5) cos 79° < cos 78°;

2)  sin 92° < sin 91°;                              6) cos 102° > cos   150° ;

3)  sin 196° > sin 201°;                           7) cos  190° < cos 200° ;

4)  sin 353° < sin 359°;                             8) cos 290° < cos 310°.

3. Какое число больше:

а)  sin 735° или  sin  (—1066°);

б)  sin (—313°) или sin 790°;

в)  cos 860° или  cos  510°;

r) cos  (—20°) или cos (—10°)?

4. В каких четвертях может оканчиваться угол φ, если:
a) sin φ cos φ > 0; б) sin φ cos φ < 0?

5. В каких четвертях может оканчиваться угол φ, если:
a) cos 2φ > 0, sin 2φ < 0;          б) cos 2φ < 0, sin 2φ > 0?

6. В каких четвертях может оканчиваться угол а, если:

а)  |sin а| = —sin а;
б)  |cos а| = cos а;
в)  |sin  (—а)| = —sin а ?

7. Расположить  в  порядке возрастания  величины;

а)  sin (—55°); sin 600°; sin 1295°;
б)  cos 654°; cos (—67°); cos 295°.

8.Как изменяется sin 2φ при изменении угла φ:

а)  от 0° до 45°;                 и) от 135° до 180°;

б)  от 90° до 135° ;              г) от 5760° до 5805°?

9.  Как изменяется cos 3φ при изменении угла  φ от   3660° до 3690°?

Изменение функций tg φ и ctg φ

Изменение функций tg φ

Для полного исследования функции tg φ достаточно изучить ее лишь в интервале от —90° до 90°.

При φ = ±90° tg φ не определен. Но если угол φ, оставаясь в пределах от —90° до 90°, хоть немного отличается от ±90°, то выражение tg φ уже определено. Посмотрим, как же ведет себя функция tg φ, когда ее аргумент φ близок к ± 90°.

По мере того как угол φ приближается к 90°, оставаясь меньше 90°, ордината соответствующей точки на оси тангенсов  неограниченно возрастает.

Какое бы большое число N мы ни взяли, всегда можно указать такой угол φ₀ , что для всех острых углов φ, больших φ₀, будет: tg φ > N. Этосвойство тангенсов условно записывается так:

lim tg φ = + ∞
φ —>90°
(φ<90°)

(читается: предел тангенса φ, когда φ стремится к 90°, оставаясь при этом меньше 90°, равен плюс бесконечности).

По мере того как угол φ приближается к—90°, оставаясь при этом больше—90°, ордината соответствующей точки на оси тангенсов, будучи отрицательной, неограниченно возрастает по абсолютной величине .

Какое бы большое число N мы ни взяли, всегда можно указать такой угол φ₀ , что для всех углов φ, меньших φ₀, но больших— 90°, будет: | tg φ| > N, причем tg φ <0.

Это свойство тангенса условно записывается так:

lim tg φ = — ∞
φ —>  —90°
(φ >  —90°)

(читается: предел тангенса φ, когда φ стремится к —90°, оставаясь при этом больше — 90°, равен минус бесконечности).

Мы исследовали поведение функции tg φ вблизи конечных точек интервала (—90°, 90°). Исследовать tg φ внутри этого интервала весьма просто. Как уже указывалось, tg φ может принимать любые числовые значения.

Из рисунка  легко понять, что, чем больше значение аргумента φ в интервале (—90°, 90°), тем больше будет ордината соответствующей точки на оси тангенсов. Следовательно, из двух произвольных углов этого интервала большему соответствует больший   тангенс.

Углам, оканчивающимся в 1-й и 3-й четвертях, соответствуют точки на оси тангенсов с положительными ординатами . Поэтому тангенсы этих углов положительны.

Углам, оканчивающимся во 2-й и 4-й четвертях, соответствуют точки на оси тангенсов с отрицательными ординатами . Поэтому тангенсы этих  углов отрицательны.

Принято говорить, что
при увеличении угла от —90° до + 90° тангенс его возрастает от —∞ до+∞

Схематично поведение функций tg φ в интервале—90° < φ <  90° изображено сплошной линией на рисунке. Пунктирные линии на том же рисунке дают представление об изменении функции tg φ в других интервалах изменения аргумента φ. Такая картина объясняется периодичностью тангенса.

Необходимо особо отметить следующее. Если угол φ приближается к 90°, оставаясь при этом меньше 90°, то tg φ неограниченно возрастает. Если же угол φ приближается к 90°, оставаясь при этом больше 90° , то tg φ неограниченно убывает. Аналогично можно сформулировать и закон изменения функции tg φ, когда φ —> — 90°.

Изменение функций ctg φ

Аналогично можно  исследовать и функцию ctg φ.    

Нетрудно видеть , что

lim ctg φ = + ∞
φ —>0°
(φ > 0°)

lim ctg φ = — ∞
φ —> 180°
(φ < 180°)

Из двух углов,  заключенных в интервале (0°, 180°), большему соответствует    меньший    котангенс.

Котангенсы углов, оканчивающихся в 1-й и 3-й четвертях, положительны; котангенсы углов, оканчивающихся во 2-й и 4-й четвертях, отрицательны.

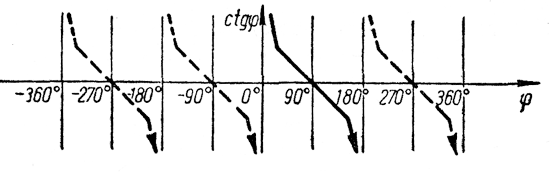
Принято говорить, что при увеличении угла от 0° до 180° котангенс его уменьшается от +∞ до — ∞

Схематично поведение функции ctgφ представлено на рисунке.

Упражнения

1. Определить   знаки   следующих   выражений:

1)  tg   153°;           4) ctg   (- 402°) • tg   1°;   7) tg (-1230°);
2)  ctg 270°;           5) tg 73°;                           8) tg 140° • ctg 240°;
3)  tg  301°;           6) ctg   (-910°);                 9) tg 546° - 1.

2. Какое число больше:

1)  tg 92°     или tg 91°;     5) ctg 102°         или ctg 150°;
2)  tg 61°     или tg 60°;      6) ctg (—313°)    или ctg 790°;
3)  tg  353°   или  tg  359°;  7) ctg   (—20°)     или  ctg   (—10°);
4) ctg 290°  или ctg 310°,   8) tg  407°           или ctg -497°?

3.   В каких четвертях может оканчиваться угол φ, если:

а)  |tg φ| = tg φ;                        в) tg 2φ > 0;
б)  |ctg (—φ)| = —ctg φ;           г) ctg 2φ < 0?

4.  В каких четвертях имеют одинаковые знаки:

а)  sin φ и tg φ;           в) cos φ и tg φ;

б)  cos φ и ctg φ;         г) tg φ и ctg φ?

5.  Какие  пары  тригонометрических функций  имеют одинаковые знаки  во всех  четвертях?

6.  Данные выражения расположить в порядке возрастания:

а)  tg (—55°); tg 600°; tg 1295°;
б)  ctg 295°; ctg (—67°); ctg 654°.

7.    Какие   тригонометрические   функции   внутреннего  угла треугольника могут принимать отрицательные   значения и когда именно?

8.   Могут ли быть отрицательными  значения  тригонометрических  функций:

а)  половины внутреннего  угла треугольника;
б)  полусуммы двух внутренних углов треугольника;
в)  полуразности двух внутренних углов треугольника?