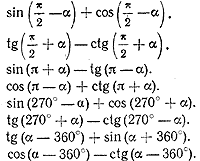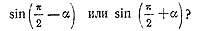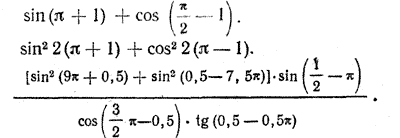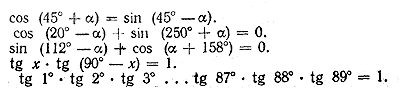ФОРМУЛЫ ПРИВЕДЕНИЯ.

Теорема.   Для любого угла φ

sin (90° — φ) = cosφ.                                      (1)

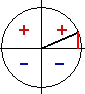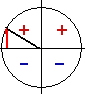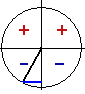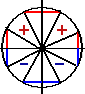
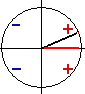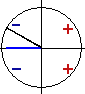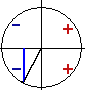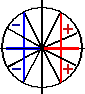
Доказательство. Если угол φ оканчивается в 1-й четверти, то угол 90° + φ должен оканчиваться во 2-й четверти.   Используя   единичный   круг, получаем:

sin (90° + φ) = BD, cos φ  = ОС.

Но треугольники ОАС и BOD равны; поэтому BD = ОС.  Отсюда и вытекает равенство (1).

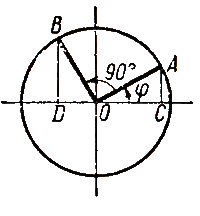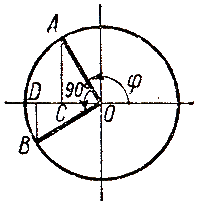
Если угол φ оканчивается во 2-й четверти, то угол 90° +φ должен оканчиваться в 3-й четверти. Используя единичный круг, получаем:

sin (90°+φ) = — BD, cos φ = —ОС.

Треугольники ОАС и BOD равны; поэтому BD = ОС. Следовательно, —BD = —ОС, или sin (90° +φ) = cos φ.

Аналогично можно рассмотреть случаи, когда угол φ оканчивается в 3-й или в 4-й четверти. Тождество (1) легко проверить и в случае, когда конечная сторона угла φ лежит на какой-нибудь оси координат. Предлагаем учащимся самостоятельно убедиться в этом.

Из доказанного тождества (1) вытекает ряд других важных тождеств. Заменив в (1) φ на — φ, получаем:

sin (90° — φ) = cos (—φ) = cos φ.                      (2)

Чтобы получить аналогичную формулу для cos (90° — φ), заменим в (2) φ на 90° — φ. В результате получаем:

или                sin  [90° — (90° — φ)] = cos   (90° — φ),

Итак,                            sin φ = cos (90° — φ).

cos (90° — φ) = sin φ.                            (3)

Из (2) и (3) вытекает:

tg (90° — φ) = ctg φ.        .                              (4)

Аналогично,                  

Формулы      

sin (90° — φ) = cos φ,    tg  (90° — φ) == ctg φ,

cos  (90° — φ) = sin φ,    ctg (90° — φ) = tg φ.

иногда называют формулами дополнительного угла. Это связано с тем, что углы 90° — φ и φ дополняют друг друга до прямого угла. Эти формулы очень просто запомнить: одна функция заменяется на другую, сходную с ней (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).

Например, sin 40° = cos 50°; tg 70° = ctg 20° и т. д.

Теперь получим формулы для угла 90° + φ. Одну из таких формул мы уже доказали выше:

sin   (90° + φ) = cos φ.

Остальные формулы легко получаются из формул дополнительного угла и свойства четности (нечетности) тригонометрических функций. Имеем:

cos (90° + φ) = cos [90° — (— φ)] = sin (— φ) = —sin φ;

 tg  (90° + φ) = tg [90°— (— φ)] = ctg(— φ) = —ctg φ;

ctg (90° + φ) = ctg [90° — (— φ)] = tg (— φ) = — tg φ.

Исходя из этих формул, можно получить формулы для углов 180° ± φ.  Например,

sin (180° + φ) = sin [90° + (90°+ φ)] = cos (90° + φ) = —sin φ;

sin (180° — φ) = sin [90° + (90° — φ)] = cos (90° — φ) = sin φ.

Аналогично доказываются формулы

cos (180° + φ) = — cos φ; cos (180° — φ) =  — cos φ.

Чтобы получить соответствующие формулы для тангенса и котангенса, можно воспользоваться выведенными соотношениями

для синуса и косинуса, учитывая, что tg φ = ^{sin φ}/_{cos φ}, ctg φ = ^{cos φ}/_{sin φ}.

Однако в данном случае лучше всего исходить из того, что угол 180° является периодом функций tg φ и ctg φ. Отсюда сразу же получаем:          

tg (180° + φ) = tg φ,

tg (180° — φ) == tg (—φ) = — tg φ,

ctg (180° + φ) = ctg φ,

ctg (180° — φ) =  ctg (— φ) = — ctg φ.

Из формул для углов 180° ± φ можно получить аналогичные формулы для  углов 270° ± φ.

Формулы для углов 360° ± φ легко получаются, если учесть, что угол 360° является общим периодом тригонометрических функций. Подробно останавливаться на этом мы не будем. В таблице приведены нужные нам формулы.

Заучивать эти формулы нет нужды. Достаточно помнить следующее:

1)  если в формуле содержатся углы 180° и 360° (π и 2π), то наименование функции не изменяется;

если же в формуле  содержатся  углы  90° и 270° (^π/₂ и ^3π/₂), то наименование функции меняется на сходное (синус на косинус, тангенс на котангенс и т. д.);

2)  чтобы определить знак в правой части формулы (+ или—), достаточно, считая угол  φ острым, определить знак  выражения, стоящего в левой части формулы.

Пусть, например, нужно определить tg (90° + φ). Прежде всего мы замечаем, что в формуле содержится угол 90°. Поэтому в правой части искомой формулы должен стоять   ctg φ.    
Чтобы определить знак перед ctg φ, предположим, что угол φ острый. Тогда угол 90° + φ должен оканчиваться во 2-й четверти. Но тангенс угла, оканчивающегося во 2-й четверти, отрицателен. Поэтому перед ctg φ нужно взять знак —.

Итак,

tg (90° + φ) = — ctg φ.

Аналогично устанавливается формула

cos (180° — φ) = — cos φ.

Поскольку в формуле содержится угол в 180°, наименование функции не изменяется. Если угол φ острый, то угол 180°—φ должен оканчиваться во 2-й четверти. Но косинус угла, оканчивающегося во 2-й четверти, отрицателен. Поэтому в правой части формулы должен стоять знак —.

Полученные выше формулы носят название формул приведения. Причины такого названия будут выяснены далее.

Упражнения

1.Упростить выражения

2.  Доказать, что если прямые у = k₁x и у = k₂x взаимно перпендикулярны, то k₁k₂ = — 1.
3.  tg x = 3. Чему равен тангенс дополнительного угла?
4.  sin φ = 0,6.  Чему равен  синус дополнительного  угла?
5. Что  больше:

6.Упростить выражения

7. Доказать тождества

8.   Доказать,   что  синус  суммы  двух   углов  треугольника равен синусу третьего угла.
9. 1) Доказать, что площадь любого четырехугольника равна   половине   произведения его   диагоналей    на    синус    угла  между  ними.
2)  Доказать, что из всех прямоугольников с  данной  диагональю наибольшую площадь имеет квадрат.
3)   Какой четырехугольник с диагоналями d₁ и d₂ имеет максимальную площадь?

10. Что больше:

а)  sin 26° или cos 40°;      в) sin 0,63 или cos 0,87 ;

б)  tg57° или ctg20°;        г) tg ³/₈ π или ctg ⁵/₁₆ π?    .