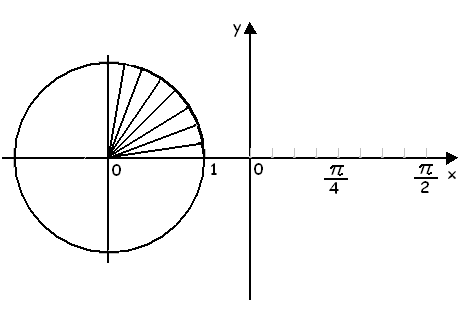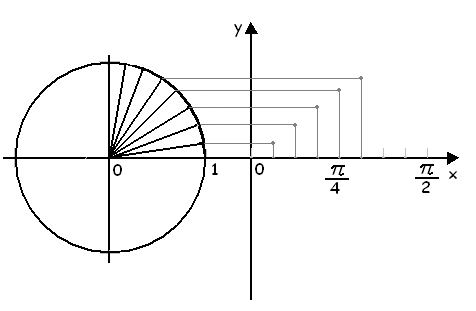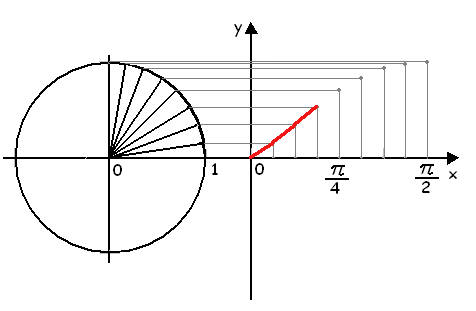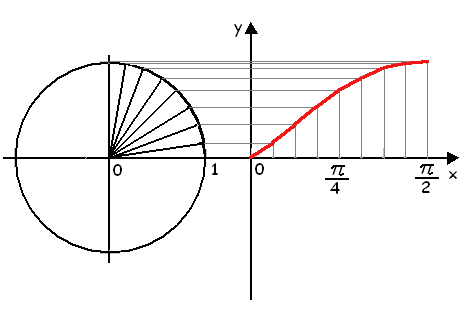График функции   у = sin x

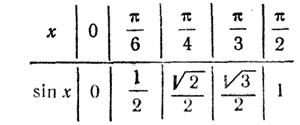
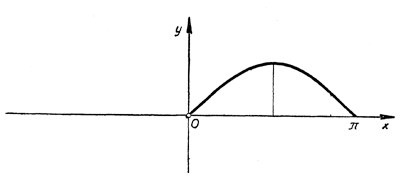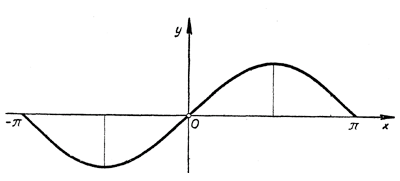
В разделе "Определение  значений тригонометрических функций любого угла" мы выяснили, что поведение тригонометрических функций, и функции у = sin х в частности, на всей числовой прямой (или при всех значениях аргумента х) полностью определяется ее поведением в  интервале    0 < х < ^π/₂ .

Поэтому прежде всего мы построим график функции у = sin х именно в этом интервале.

Составим следующую таблицу значений нашей функции;

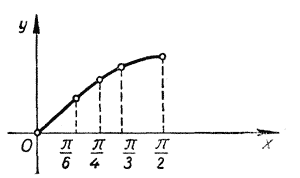
Отмечая соответствующие точки на плоскости координат и соединяя их плавной линией, мы получаем кривую, представленную на рисунке

Полученную кривую можно было бы построить и геометрически, не составляя таблицы значений функции у = sin х.

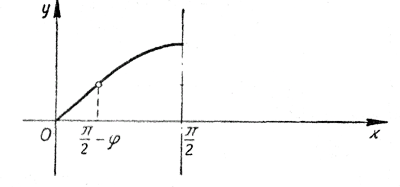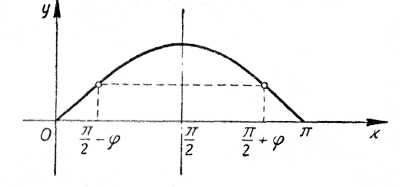
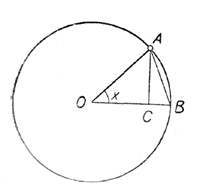
1.Первую четверть окружности радиуса 1  разделим на 8 равных частей.Ординаты точек деления окружности представляют собой синусы   соответствующих   углов.

2.Первая  четверть   окружности соответствует углам от 0 до ^π/₂. Поэтому на оси х возьмем отрезок    [0 , ^π/₂ ] и разделим его на 8 равных частей.

3.Проведем прямые, параллельные оси х, а из точек деления восставим перпендикуляры до пересечения с горизонтальными прямыми.

4.Точки пересечения соединим плавной  линией.

Теперь обратимся к интервалу ^π/₂ < х < π.
Каждое  значение аргумента  х из этого  интервала   можно   представить   в   виде

x = ^π/₂ + φ

где 0 <φ < ^π/₂ . По формулам приведения

sin ( ^π/₂ + φ) = соsφ = sin ( ^π/₂ — φ).

Точки оси х с    абциссами ^π/₂ + φ и  ^π/₂ — φ   симметричны    друг другу относительно точки оси х с абсциссой ^π/₂, и синусы в этих точках одинаковы. Это позволяет получить график функции у = sin х в интервале [^π/_{2 ,} π ] путем простого симметричного отображения графика этой функции в интервале  [0 , ^π/₂ ] относительно прямой х = ^π/₂.

Теперь,  используя свойство  нечетности функции  у = sin х,

sin  (— х) = — sin х,

легко   построить   график  этой  функции  в   интервале   [— π, 0].

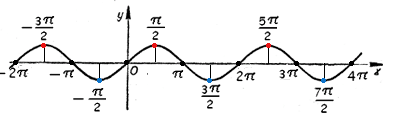
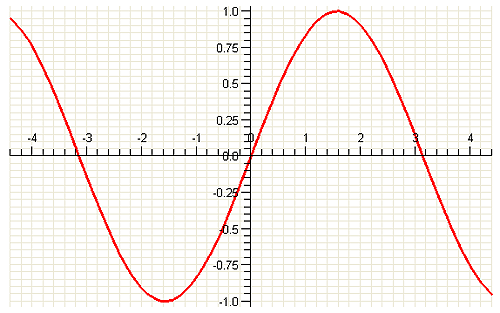
Функция у = sin х периодична с периодом 2π;. Поэтому для построения всего графика этой функции достаточно кривую, изображенную на рисунке, продолжить влево и вправо периодически  с  периодом   2π.    

Полученная в   результате   этого кривая  называется синусоидой. Она и представляет собой график функции у = sin х.

Рисунок  хорошо иллюстрирует все те свойства функции у = sin х, которые раньше были доказаны нами. Напомним эти свойства.

1)   Функция у = sin х определена для всех значений х, так что областью ее определения является совокупность всех действительных чисел.

2)   Функция у = sin х ограничена. Все значения, которые она принимает, заключены в интервале от —1 до 1, включая эти два  числа.  Следовательно,   область   изменения   этой   функции определяется неравенством  —1< у < 1. При х = ^π/₂ + 2kπ функция принимает   наибольшие   значения,   равные  1,   а   при   х = — ^π/₂ + 2kπ — наименьшие значения, равные — 1.

3)   Функция у = sin х   является нечетной (синусоида симметрична относительно начала координат).

4)  Функция у = sin х периодична с периодом 2π.

5)  В интервалах 2nπ < x < π + 2nπ (n — любое целое число) она   положительна,   а   в   интервалах   π + 2kπ < х < 2π + 2kπ (k — любое целое число) она отрицательна. При х = kπ функция обращается в нуль. Поэтому эти значения аргумента х (0; ±π; ±2π; ...) называются нулями функции у = sin x

6)   В интервалах   — ^π/₂ + 2nπ < х < ^π/₂  + 2nπ  функция у = sin x монотонно   возрастает,   а  в   интервалах  ^π/₂ + 2kπ < х < ^3π/₂  + 2kπ  она   монотонно убывает.

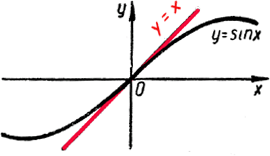
Cледует    особо   обратить   внимание на поведение функции у = sin x вблизи точки х= 0.

Как видно из рисунка , в окрестности точки х = 0 синусоида почти сливается с биссектрисой 1-го и 3-го координатных углов. Поэтому при малых углах х, выраженных в радианах, или при малых по абсолютной величине числовых значениях х (как положительных, так и отрицательных) sin x ≈  x.

Например, sin 0,012 ≈ 0,012; sin (—0,05) ≈ —0,05;

sin 2° = sin   ^{π • 2}  /₁₈₀ = sin  ^π/₉₀  ≈ 0,03 ≈ 0,03.

Вместе с тем  следует   отметить,   что   при   любых   значениях   х

| sin x |  <  | x |.                             (1)

Действительно, пусть радиус окружности, представленной на рисунке, равен 1,
a   /  AОВ = х.

Тогда sin x = АС. Но АС < АВ, а АВ, в свою очередь, меньше длины дуги АВ, на которую опирается угол х. Длина этой дуги равна, очевидно, х, так как радиус окружности равен 1.  Итак,  при 0 < х < ^π/₂

sin х < х.

Отсюда в силу нечетности функции у = sin x легко показать, что при — ^π/₂ < х < 0

| sin x |  <  | x |.  

Наконец,  при x = 0

| sin x | = | x |.

Таким образом, для | х | < ^π/₂ неравенство (1) доказано. На самом же деле это неравенство верно и при  | x | > ^π/₂  в силу того, что | sin х | < 1,   а  ^π/₂ > 1

Упражнения

1.По графику функции у = sin x определить: a) sin 2;  б) sin 4; в) sin (—3).

2.По графику функции  у = sin x определить,   какое число из интервала
[ —  ^π/_{2 ,}  ^π/₂] имеет синус, равный:  а) 0,6;   б) —0,8.

3.  По графику функции  у = sin x определить,   какие числа имеют   синус,  
 равный ¹/₂.

4.  Найти приближенно (без использования таблиц): a) sin 1°;   б) sin 0,03;   
в) sin (—0,015);   г) sin (—2°30').