График функции   у = cos x

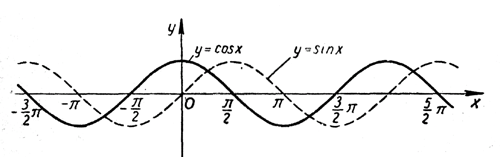
Как мы   знаем,   cos х = sin (х + ^π/₂).

Поэтому если cos x принимает некоторое значение а при х = х₀, то при х = х₀ + ^π/₂ это же значение а примет и sin x. Если аргумент х толковать как время, то можно сказать, что значения функции   у = sin x  как   бы   «запаздывают»,   или   «отстают»   от соответствующих значений функции у = cos x на ^π/₂.      

Отсюда можно заключить, что график функции у = cos x получается посредством сдвига графика функции у = sin x вдоль оси абсцисс влево на расстояние ^π/₂.

Итак, график функции у = cos x есть синусоида, сдвинутая влево на ^π/₂. Иногда такую кривую называют косинусоидой.

Косинусоида хорошо иллюстрирует все основные свойства функции у = cos х, которые раньше были нами доказаны. Предлагаем учащимся еще раз сформулировать эти свойства и дать им графическую интерпретацию.

Упражнения

1.По графику функции у = cos х определить: a) cos 3;  б) cos 4; в) cos (—2).

2.  По графику функции у = cos х определить, какое число из интервала  [0, π] имеет косинус, равный:  а) 0,6;  б)  —0,8.

3.По графику функции у = cos x определить, какие числа имеют косинус,  равный ¹/₂.

4.   При малых  (по абсолютной величине) значениях х косинусоида у = cos х имеет примерно такой же вид, как и парабола  у = 1 — 0,5x² (Сделайте чертеж!) Поэтому для малых значений х

cos x ≈ 1 — 0,5x².

Используя  эту формулу,  вычислите приближенно:

a) cos 1°; б) cos 0,03;. в) cos (—0,015); г) cos (—2°30'). Полученные результаты сравните с результатами вычислений на калькуляторе или в программе Excell .