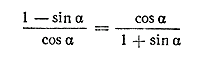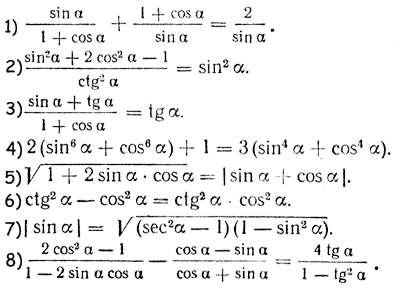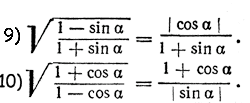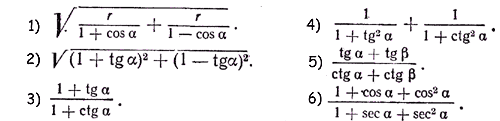| 3ГОНОМЕТРИЯ В НАЧАЛО |
|
Доказательство тригонометрических тождеств При доказательстве любых тождеств, и в частности тригонометрических, обычно используют следующие способы: 1) выражение, стоящее и одной части равенства, с помощью тождественных преобразований приводят к выражению, стоящему в другой части равенства; 2) выражения, стоящие в левой и правой частях тождества, с помощью тождественных преобразований приводят к одному и тому же виду; 3) доказывают, что разность между левой и правой частями данного тождества равна нулю. Поясним это на некоторых частных примерах. Пример 1. Доказать тождество sin4α — cos4α = sin2 α — cos2 α . Используя формулу для разности квадратов двух чисел, получаем: sin4α — cos4α = (sin2α + cos2α) (sin2α — cos2α). Ho sin2α + cos2α = 1. Поэтому sin4α — cos4α = sin2α — cos2α, что и требовалось доказать. |
|
Пример 2. Доказать тождество
Это тождество мы будем доказывать путем преобразования выражения, стоящего в правой части. Способ 1.
Поэтому Способ 2. Прежде всего заметим, что ctg α =/= 0; в противном случае не имело бы смысла выражение tg α = 1/ctg α. Но если ctg α =/= 0, то числитель и знаменатель подкоренного выражения можно умножить на ctg α, не изменяя значения дроби. Следовательно,
Используя тождества tg α • ctg α = 1 и 1+ ctg2α = cosec2 α , получаем
Поэтому Замечание. Следует обратить внимание на то, что левая часть доказанного тождества (sin α) определена при всех значениях α, а правая — лишь при α =/= π/2 n. Поэтому только при всех допустимых значениях α Пример 3. Доказать тождество sin (3/2 π + α ) + cos ( π - α ) = cos ( 2π + α ) - 3sin (π/2 - α ) Преобразуем левую и правую части этого тождества, используя формулы приведения: sin (3/2 π + α ) + cos ( π - α ) = — cos α — cos α = — 2 cos α; cos ( 2π + α ) - 3sin (π/2 - α ) = cos α — 3 cos α = — 2 cos α. Итак, выражения, стоящие в обеих частях данного тождества, приведены к одному и тому же виду. Тем самым тождество доказано. Пример 4. Доказать тождество sin4 α + cos4 α — 1 = — 2 sin2α cos2α. Покажем, что разность между левой и правой частями. данного тождества равна нулю. Имеем: (sin4 α + cos4 α — 1) — (— 2 sin2α cos2α) = (sin4 α + 2sin2α cos2α + cos4 α) — 1 = = (sin2α + cos2α)2 — 1 = 1 — 1 = 0. Тем самым тождество доказано. Пример 5. Доказать тождество
Это тождество можно рассматривать как пропорцию. Но чтобы доказать справедливость пропорции a/b = c/d, достаточно показать, что произведение ее крайних членов ad равно произведению ее средних членов bc. Так мы поступим и в данном случае. Покажем, что (1 — sin α) (1+ sin α) = cos α • cos α. Действительно, (1 — sin α) (1 + sin α) = 1 —sin2α = cos2α. По поводу этого примера можно было бы сделать замечание, аналогичное замечанию к примеру 2. Упражнения I . Доказать тождества
II . Упростить выражения
III. 1). Найти значение выражения 2). Найти значение выражения 3). Найти значение выражения IV. Доказать тождества
|
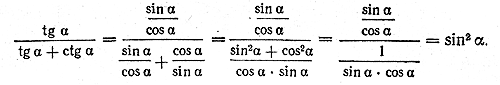
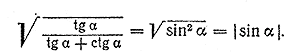
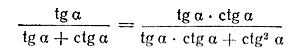
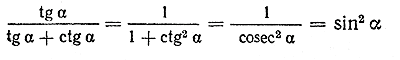
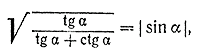 что и требовалось доказать.
что и требовалось доказать.