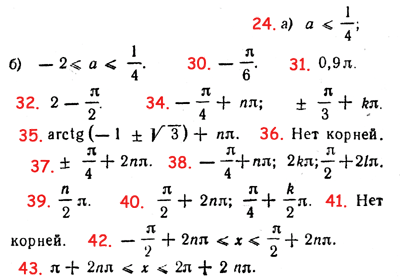Задачи на повторение

Доказать тождества

1.   (r cos α )² + (r sin α sin β)²+ (r sin α cos β)² = r².

2.      

3.          

4.  1 + (ctg²α — tg²α) • cos²α = ctg²α.

Решить данные    неравенства  относительно острого   угла  α:

5.     cos(α — 120°) > sin (64° + α).

6.* tg (65° — 2α) > ctg (40°— α).

7*.   sin  (α + 30°) > cos  (72° — 2α).

8.   Найти косинус, тангенс и котангенс угла φ, если   известно,  что sin φ = 0,28.

9.  Найти синус, тангенс и котангенс угла φ, если известно, что cos φ = —0,96 и угол φ оканчивается не в 3-й четверти.

10.  Найти синус, косинус и котангенс угла φ, если известно, что этот угол оканчивается в 3-й четверти и tg φ = ¹/₃

Найти синусы,  косинусы, тангенсы и котангенсы следующих углов:

11.  arcsin 0,28 и  arcsin (—0,28).

12.  arccos 0,96 и arccos (—0,96).

13.  arctg ⁵/₁₂    и   arctg  (— ⁵/₁₂)

14.  arcctg 1 ¹/₃   и arcctg ( — 1 ¹/₃ )

Упростить данные выражения :

15.  sin ( ^π/₂  — arccos 0,б) .

16.  cos[ ^π/₂  + arccos (— 0,8) ].

17. tg [ ^3π/₂ — arcsin ( — ⁵/₁₃ )]

18. sin (arctg 0,75 — ^3π/₂ ).

19. a) sin α = sin β. Можно ли сказать, что α = β?

б)  sin α = sin β, причем углы α и β оканчиваются в одной  и той же четверти. Можно ли сказать, что α = β?

в)  sin α = sin β, причем  0 < α <π и 0 < β < π. Можно ли сказать,  что α = β?

г)  sin α = sin β, причем  — ^π/₂< α <^π/₂     и   — ^π/₂ <β< ^π/₂   Можно ли сказать, что α = β?

20. Чем отличаются друг от друга функции у = х и у = sin (arcsin х)?
Сравните  графики  этих функций.

21*. Построить график функции у = arccos (cos x).

22*. На плоскости хОу найти множество всех точек,   координаты  (х,  у)   которых  удовлетворяют  условию    sin (х + у) = 0.

23. При каких значениях α определены выражения:

24. При каких значениях а данные уравнения имеют корни:

a) tg² х + tg x + а = 0;          б) sin²x + sin x + а = 0?

Проверить данные равенства :

25. arcsin (sin 1) = 1.

26. arcsin (sin 2) = π — 2.

27. arccos (cos 1,5) = 1,5.

28. arccos  (cos 2,5) = 2,5.

29.   Доказать тождества:

а)  arcsin x + arccos x = ^π/₂;

б)  arctg x + arcctg x = ^π/₂

Вычислить :

30.  arctg (ctg  ^2π/₃ ).

31.  arcctg (tg 0,6π).

32.  arccos (sin 2).

33.   Что   больше:

а)  arccos ²/₃   или   arcsin ³/₄

б)  arccos (— ⁴/₅)  или arccos (— ⁵/₆)

в)   arctg 3 или  arctg 4?

Решить данные уравнения :

34.   tg³ x + tg² x — 3tg x = 3.

35.   3sin² x + 2 sin x cos x = 2.

36.  sin x — cos 2x + sin 4x = 3.

37.  cos x = \/2 sin 2x.

38.  sin x + cos x = 1 + 2 sin x cos x.

39.  sin (π cos x) = 0.

40.  cos 2x sin x = cos 2x.

41.

42.  \/ 1 - sin² x   = cos x.

43.   \/ 1 - cos² x   = — sin x.

44.   Доказать,   что   уравнение

sin x + sin 2x +  sin 3x + ... + sin 100x = 100

не имеет корней.

ОТВЕТЫ