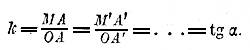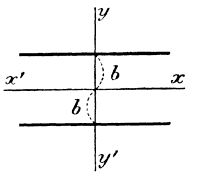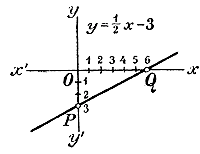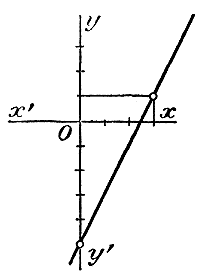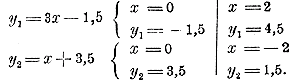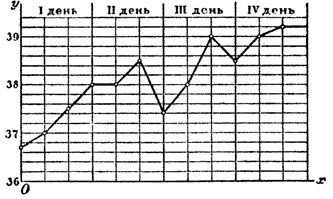
ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ФУНКЦИЙ.

106. Понятие о функции. Если какая-нибудь величина зависит от некоторой другой величины, то принято говорить, что первая величина есть функция второй (или от второй). Так вес воды, наполняющей какой-нибудь сосуд, конечно, зависит от вместимости этого сосуда (при изменении вместимости изменяется и вес воды); поэтому можно сказать, что этот вес есть функция вместимости сосуда; вес керосина, сгорающего в лампе, есть функция от времени, в течение которого горит лампа; длина хорды, проведенной в круге, есть функция расстояния этой хорды от центра круга, и т. д.

Если величина, от которой другая величина есть функция, может быть изменяема произвольно, то она называется переменной независимой (величиной).Пеpемeнная независимая называется также аргументом функции.; сама же функция может быть названа переменной зависимой .

Если, напр., мы рассматриваем зависимость длины хорды данного круга от ее расстояния от центра, то это расстояние есть величина переменная независимая, а длина хорды, которая есть функция от этого расстояния, представляет собой переменную зависимую. Те величины, которые предполагаются неизменяющимися, называются величинами постоянными. Напр., при исследовании зависимости между длиною хорды круга от ее расстояния от центра мы предполагаем, что длина радиуса этого круга не меняется; тогда эту длину можно рассматривать как постоянную.

Функции бывают не только от одной переменной независимой, но и от двух, трех и более. Напр., длина пути, пройденного поездом железной дороги, зависит и от скорости, с какою движется этот поезд, и от времени, в течение которого был пройден путь; значит, длина пути в этом случае есть функция от двух переменных независимых: скорости и времени.

Зависимость между функцией и переменными независимыми часто может быть выражена формулой, связывающей между собою числа, измеряющие эти величины. Так, мы видели, что прямая пропорциональная зависимость выражается формулой: y = kx, обратная пропорциональная зависимость выражается формулой: у = ^k_/x , и т.п.

Если функция зависит от одного переменного независимого числа (о таких функциях мы и будем теперь говорить), то это число обозначается большею частью буквою х, а сама функция — буквою у. Числа, которые предполагаются постоянными, мы будем обозначать первыми буквами алфавита: а, b, с.

Когда мы рассматриваем зависимость между функцией и переменным независимым числом x, нам важно ясно представлять себе не только то, что функция изменяется при изменении переменного независимого числа, но и то, как происходит это изменение. При этом нет надобности, чтобы функция была задана в виде какого-либо алгебраического выражения; она может быть задана несколькими своими значениями, найденными, положим, из опыта. Примеры таких эмпирических (опытных) функций указаны в следующем параграфе.

107. Графики температуры, влажности и пр. При лечении многих болезней доктору очень важно знать, как изменяется температура больного в течение хода болезни. Для этого пользуются особым медицинским термометром Цельсия, на котором проставлены градусы (от 35° до 42°), разделенные на десятые доли. Термометром этим измеряют температуру больного по несколько раз в день, напр, утром, среди дня и вечером, и результаты измерения записывают. Положим, напр., температура больного за первые 4 дня болезни была следующая :

Чтобы процесс изменения температуры в зависимости от времени сделать наглядным, прибегнем к графическому его изображению.

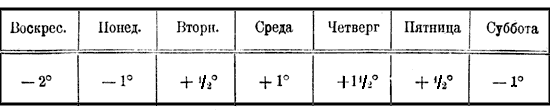
Для этого на горизонтальной прямой Ох отложим произвольной длины равные деления, которые будут у нас означать промежутки времени между двумя последовательными измерениями температуры. На другой прямой Оу, перпендикулярной Ох, также отложим произвольной длины равные деления и условимся, что каждое из них будет соответствовать, положим, 0,2 градуса температуры. Внизу поставим 36° (предполагая, что температура больного не будет ниже 36°), затем через 5 делений 37°, потом снова через 5 делений 38° и т. д. Проведя затем из всех точек, разграничивающих деления, прямые, параллельные линиям Ох и Оу, мы легко нанесем на полученную таким образом сетку точки, соответствующие наблюденным температурам. Так, на первомслева перпендикуляре возьмем точку соответствующую (приблизительно) 36,7°, на втором перпендикуляре — точку, соответствующую 37°, и т. д. Проведя через все полученные точки ломаную линию, мы получим график (чертеж) температуры больного; этот график наглядно изображает нам процесс изменения температуры за 4 первых дня болезни.

В приведенном нами примере температуры больного отрезки, откладываемые на прямых Ох и Оy, выражались положительными числами. Но иногда бывает необходимо откладывать и отрицательные отрезки. Положим, напр., мы наблюдали температуру наружного воздуха в течение недели ежедневно в полдень и результаты записали в такой таблице:

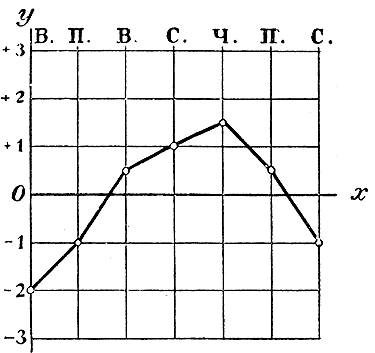
Чтобы выразить изменение этих температур графиком, придется откладывать температуры — и положительные, и отрицательные. Это можно сделать, если условимся положительные температуры откладывать вверх от точки О, а отрицательные вниз от нее. Тогда мы получим такой график

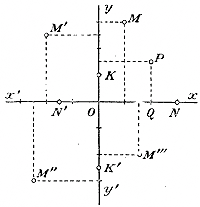
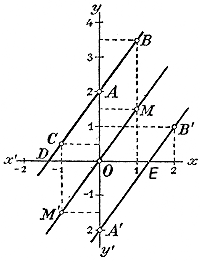
Подобно этому часто составляют графики влажности воздуха, графики атмосферногодавления и пр. Существуют даже самопишущие приборы, которые, раз пущенные в ход, сами собой вычерчивают на особой бумаге кривую температуры воздуха или кривую атмосферного давления и т. п.

Мы перейдем теперь к более подробному рассмотрению графического изображения функций; мы увидим при этом, что изображенные на чертеже функции представляются нам значительно яснее, чем мы их представляли себе без чертежа.

Ознакомимся сначала с тем, что называется координатами точки, расположенными где-нибудь на данной плоскости.

108. Координаты точки. Возьмем две взаимно перпендикулярные прямые хх' и yy' , пересекающиеся в точке О.

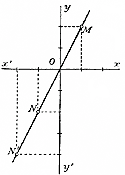
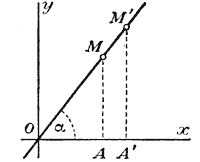
Примем, далее, какой-нибудь отрезок прямой (равный,, напр., сантиметру) за единицу длины и условимся откладывать значения переменного независимого числа х на прямой хх', начиная от точки О, как начала, причем положительные значения х будем откладывать вправо от О, а отрицательные — влево от О. Таким образом, отрезок ОА выразит нам значение х, равное +1, отрезок ОВ — значение х, равное + 2, отрезок OC —значение х, равное — 3, и т. п. Сама точка О представляет значение, равное нулю. Значения функции у, соответствующие этим значениям x , мы условимся откладывать на прямых, проведенных через точки A, B, С,... параллельно уу' (иначе сказать, на перпендикулярах к прямой хх'), причем положительные значения функции мы будем откладывать вверх от прямой хх' а отрицательные — вниз от нее. Если, напр., при х = ¹/₂ значение функции у будет + 1¹/₄, то на прямой хх' мы возьмем отрезок ОD = + ¹/₂, и восстановим перпендикуляр DE, равный + 1¹/₄ тогда получим точку Е, которая выразит нам значение y = + 1¹/₄ при x = + ¹/₂. Равным образом, точка К выразит значение у, равное—1³/₄ при х = — 2¹/₂ и т. п.

Заметим, что точки Е, К,... мы можем получить несколько иначе, а именно, вместо того, чтобы на перпендикулярах DE, FK,... откладывать отрезки, выражающие значения у, мы можем их откладывать на прямой уу' начиная от точки О, и затем из концов этих отрезков проводить прямые, параллельные хх' до пересечения с соответствующими перпендикулярами.

Так, OL = + 1¹/₄ и проведя LE || Ох, мы получим точку Е, т. е. ту самую, точку, которую раньше мы получили, отложив DE = + 1¹/₄

To же самое можно сказать о точке K и о всех других подобных точках. Вот почему горизонтальнyю прямую принято обозначать буквами хх' а вертикальную — буквами уу': на первой откладываются значения переменного независимого числа х, на второй можно откладывать значения функции у.

Отрезки OD, OF, ..., откладываемые на прямой хх' и выражающие значения переменного независимого числа х, называются абсциссами (ОD — абсцисса точки Е, OF — абсцисса точки К и т. д.); отрезки DE, FK,..., откладываемые на перпендикулярах к хх' (или на прямой уу') и выражающие значения функции у, называются ординатами (DE -ордината точки Е, FK - ордината точки К и т.д.); те и другие совместно называются координатами точек Е, К.

Неограниченная прямая хх' ,на которой откладываются абсциссы, называется осью абсцисс или осью x-ов (ось иксов); неограниченная прямая уу', на которой (или параллельно которой) откладываются ординаты, называется осью ординат или осью y-ов (ось игрекoв); та и другая прямая совместно называются осями координат. Точка О называется началом координат .(Определение положения точки на плоскости посредством двух указанных координат введено было французским математиком Рене Декартом (1590 г.— 1650 г.), почему координаты эти называются декартовыми.)

Очевидно, что при данных координатных осях и при данной единице длины каждой паре чисел, принятых за координаты, соответствует на плоскости одна определенная точка.

Например, как видно из чертежа , следующим парам чисел (1, 3), (—2, 2¹/₂), (—2¹/₂,—3), (1¹/₂, —2) (принято из двух чисел, поставленных в скобках, первое число принимать за абсциссу, а второе — за ординату) соответствуют точки: М, М' М", М'''. И, наоборот, каждой точке плоскости соответствует определенная пара чисел, которую можно принять за координаты этой точки.

Например, если возьмем какую-нибудь точку Р, то, опустив из нее на ось x - ов перпендикуляр PQ и измерив принятой единицей отрезки OQ и PQ, мы получим абсциссу и ординату этой точки (на нашем чертеже у точки Р абсцисса оказывается + 2 и ордината + ¹/₂). Если возьмем точку на оси x - ов, то ордината ее, очевидно, будет нуль, а абсцисса—положительное или отрицательное число, измеряющeе ее расстояние от точки О; таковы, например, точки N (3,0) и N' (—1¹/₂, 0). Если точка взята на оси у-ов, то ее абсцисса равна нулю, а ордината есть число, измеряющее ее расстояние от О; таковы, например, точки К (0, +1) и К' (0,—2¹/₂).

У начала координат абсцисса и ордината, очевидно, равны нулю.

Покажем теперь, как, пользуясь такими координатами, можно наглядно изобразить изменение данной функции при помощи ее графика. Начнем с самой простой функции.

График пропорциональной зависимости (прямой и обратной).

109. График пропорциональной зависимости. Как мы видели (отдел2§ 103), пропорциональная зависимость (прямая) выражается формулой у = kх, в которой k есть постоянное число (коэффициент пропорциональности). Предположим, что k = 2 и мы желаем графически изобразить функцию: у=2х. Для этого дадим переменному числу х какие-нибудь частные значения, например такие: х = 0, 1, 2, 3,... и вычислим соответствующие значения функции y. Для ясности расположим те и другие в такой таблице:

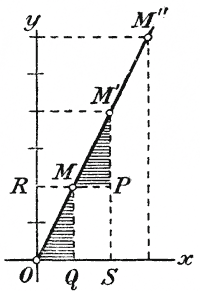
Конечно, мы не можем поместить в таблице всевозможные значения х и у, так как всех значений, очевидно, бесчисленное множество. Однако мы легко можем сообразить, что если х изменяется, положим, от 2 до 3 непрерывно (т. е. переходя через все возможные числа, заключенные между 2 и 3), то у будет изменяться тоже непрерывно (переходя через все возможные числа, заключенные между 4 и 6). Например, при таком изменении числа х функция у может сделаться равной 4,1; для этого нужно только, чтобы число х сделалось равным 4,1 : 2, т. е. 2,05, что непременно произойдет при непрерывном изменении х от 2 до 3. Таким образом, хотя наша таблица содержит только некоторые значения х и у, мы из нее все-таки видим, что когда х получит какое-нибудь значение, промежуточное между указанными в таблице, то и у получит значение, промежуточное между указанными в таблице.

Теперь, начертив координатные оси и выбрав единицу длины (положим OQ ), построим точки О, M, M', М'',..., координатами которых служат значения х и у, помещенные в нашей таблице.

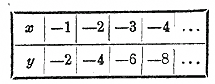
Так, О будет точка, имеющая координаты х = 0, у = 0, точка М имеет координаты х = 1, y= 2, и т. д. Сколько бы мы таких точек ни построили, все они должны лежать на одной и той же прямой. Для доказательства этого возьмем какие-нибудь 3 соседних точки, например О, М и M', и, соединив прямыми точку О с M и затем точку М с М' покажем, что прямая ММ' составляет продолжение прямой ОМ.

Для этой цели проведем МР (продолжение MR) и сравним между собою 2 прямоугольных тр-ка (покрытые штрихами).

У них OQ = MP = l и MQ = M'P = 2, и потому тр-ки равны, и, следовательно, / М'МР= / MOQ; поэтому прямая ММ' составляет продолжение прямой ОМ. Значит, три точки О, М и М' лежат на одной прямой. Все сказанное об этих трех точках может быть повторено о всяких других трех соседних точках; значит, все точки должны лежать на одной прямой.

Чтобы сделать доказательство общим, можем рассуждать так. Назначим для х два произвольных числа: х = а и х = b; тогда для у получим два соответствующих значения: y = kа и y = kb.

Пусть OQ = a, OS = b, QM=ka и SM' = kb. Проведя прямые OM и OM', мы получим два тр-ка OQM и OQM', которые подобны, так как они содержат по равному углу (прямому), лежащему между пропорциональными сторонами (OQ :OS = a и QM : SM' = ka : kb = а:b). Вследствие этого / MOQ = / M'OS, и потому точки О, М и M' лежат на одной прямой. Таким образом, всякие две точки (M и M'), удовлетворяющие формуле y = kx, оказываются лежащими на прямой, проходящей через О.

Итак, график пропорциональной зависимости (у = kх) есть прямая, проходящая через начало координат и через точку (M), у которой абсцисса есть 1, а ордината равна коэффициенту пропорциональности (в нашем примере она равна 2).

110. Замечание. Если в функции у=2х мы будем давать числу х отрицательные значения, например такие:

Тогда график функции будет прямая ON', расположенная в угле x'Oy' и составляющая продолжение прямой ОМ, построенной нами раньше.

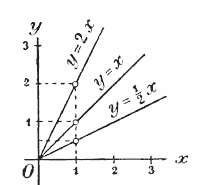
111. Изменение положения прямой в зависимости от коэффициента пропорциональности. Построим еще на одном и том же чертеже прямые, выражающие функции:

у которых коэффициенты положительные и притом возрастают.

Из чертежа мы видим, что по мере возрастания коэффициента пропорциональности прямая отклоняется все более и более от оси x- ов, приближаясь к оси у-ов. Таким образом, коэффициент k в функции у = kх характеризует собою угол, составленный прямою с полуосью Ох; поэтому число k называется также угловым коэффициентом прямой, выражающей графически функцию у = kх.

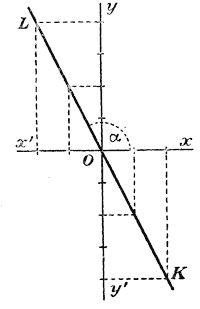
Так как из этой функции видно, что k = ^y/_x,то можно сказать, что угловой коэффициент равен отношению какого-нибудь значения функции (какой-нибудь ординаты) к соответствующему значению переменного независимого (к соответствующей абсциссе), так что если функция изображается прямою ОМ , то

(Как известно из геометрии, в прямоугольном тр-ке отношение одного катета к другому катету равняется тангенсу угла α, противолежащего первому катету.)

Полезно заметить, что если k =1, т. е. если функция имеет вид: у = х, то прямая, изображающая ее, есть биссектриса прямого угла хОу (тогда тр-к ОАМ, равнобедренный, и /_ α = 45°). Если k = 0, т. е. если функция имеет вид: у = 0, то прямая сливается с осью Ох.

Положим теперь, что коэффициент k будет отрицательное число, например у = — 2х. Тогда положительным значениям х будут соответствовать отрицательные значения у, и наоборот:

Тогда мы получим прямую KL, расположенную в углах х'Оу и xOy'.

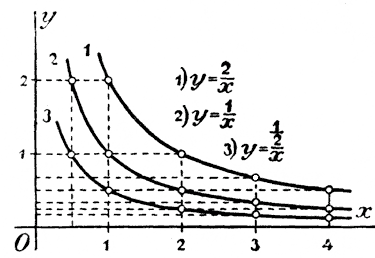
В этом случае угол, образованный прямой с полуосью Ох, будет тупой LOx, и тангенс его равен —2.

Значит, когда коэффициент k положительный, тогда прямая подымается вверх (от точки О вправо), когда же коэффициент отрицательный, прямая опускается вниз.

112. График обратной пропорциональности. Такая пропорциональность выражается, как мы видели (отдел2 § 105), формулой:

Построим график частного случая, когда k = 6 , т. е, когда функция будет: у = ⁶/_x.

Составим таблицу значений этой функции, например такую:

По поводу этой таблицы мы и здесь можем сделать такое же замечание, какое делали раньше, когда говорили о графике функции у = 2х, а именно: если х будет переходить через все возможные значения, промежуточные между указанными в таблице, например через значения, заключающиеся между 1 и 2, то и у будет получать промежуточные значения, заключающиеся между 6 и 3. 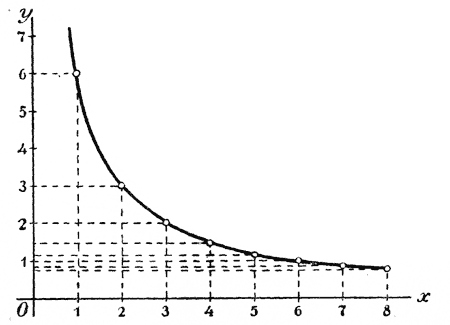Например, у может при этом сделаться равным 5¹/₂; для этого надо только, чтобы число х получило значение, при котором ⁶/_x= 5¹/₂, т. е. чтобы
х = 6: 5¹/₂, = 6 : ¹¹/₂ = ¹²/₁₁ = 1¹/₁₁что, конечно, произойдет при непрерывном изменении x от 1 до 2.

Нанеся значения, указанные в таблице, на чертеж и обведя все полученные на графике точки непрерывной кривой (от руки или помощью особой чертежной линейки, называемой лекалом), мы получим график обратной пропорциональной зависимости у = ⁶/_x .

Обратим внимание на следующие особенности этого графика: при неограниченном увеличении абсциссы х (х = 9, 10, 11, 12,...), ордината кривой все уменьшается, приближаясь к нулю, так что кривая, по мере ее продолжения направо, все ближе и ближе подходит к оси x-ов, но, однако, никогда ее достигнуть не может (дробь ⁶/_x никогда не может сделаться равной нулю). Равным образом, если для х будем брать дроби ¹/₂, ¹/₄, ¹/₈ и т.д. все приближающиеся к нулю, то у будет все более и более возрастать (y=12, 24, 48,...), так что ветвь кривой, при продолжении ее налево, неограниченно подымается вверх, приближаясь в то же время все более и более к оси y-ов, но достигнуть ее никогда не может (при х = 0 дробь ⁶/_x перестает существовать).

Чертеж , сделанный в более крупных единицах, чем предыдущий чертеж, представляет три графика функции у = ^k/_xпри k = 2, 1, ¹/₂ .Они имеют те же особенности, как и график предыдущего чертежа, отличаясь друг от друга только большею или меньшею вдавленностью к вершине прямого угла.

Вообще, график функции у = ^k/_xесть так называемая гипербола, со свойствами которой мы ознакомимся впоследствии. Заметим, что для таких чертежей всего удобнее брать так называемую канвовую (сетчатую) бумагу, которая равноотстоящими горизонтальными и вертикальными прямыми разделена на малые квадратики (например на квадратные миллиметры; тогда бумага называется миллиметровою). Прямые Ох и Оу надо брать на этой бумаге так, чтобы они совпадали с какими-либо ее прямыми. За единицу длины тогда берут одно или несколько делений бумаги (например на миллиметровой бумаге — миллиметр или сантиметр).

113. Задача. Длина железного стержня при температуре 0° составляет 1 метр; определить, какая длина l окажется у этого стержня, когда он будет нагрет до t°, если известно, что о каждым градусом нагревания длина стержня увеличивается на 0,000012 той длины, которую стержень имеет при 0°.

При нагревании на один градус длина стержня, равная при 0° одному метру (= 100 см), должна увеличиться на 100 • 0,000012 см, т. е. 0,0012 см. Удлинение при нагревании на t° должно быть в t раз более, чем при нагревании на один градус; поэтому все удлинение будет 0,0012t см. Приложив это удлинение к начальной длине стержня (при 0°), т. е. к 100 см, получим длину при температуре t

Если температуру t, до которой нагрет стержень, будем рассматривать как переменную величину, то длину l мы можем рассматривать как функцию температуры. Обозначая, по общепринятому, переменную независимую величину через х, а функцию буквою у, мы можем зависимость между длиною стержня и его температурой выразить такою формулой:

114. Двучлен первой степени. Алгебраическое выражение, представляющее собою двучлен, в котором один член содержит переменное число (в первой степени), а другой член есть число постоянное, называется двучленом первой степени. В приведенной выше задаче длина стержня выражается двучленом первой степени относительно температуры. Функции такого рода часто встречаются при решении многих задач и вопросов. Общий вид двучлена первой степени может быть выражен так:

где буквы а и b обозначают постоянные числа, положительные или отрицательные (иногда и нуль), а x — переменное число, способное принимать всевозможные численные значения; буква у означает величину самого двучлена, соответствующую взятой величине х.

Корнем двучлена называется то значение переменного числа х, при котором двучлен обращается в нуль. Чтобы найти такое значение, надо приравнять двучлен нулю и решить получившееся от этого уравнение.

Так, корень двучлена 1¹/₂x + 2 получится, если решим уравнение 1¹/₂x + 2 = 0:

115. График двучлена первой степени. Возьмем какой-нибудь частный случай двучлена, например:

Отбросим пока число 2 и возьмем более простую функцию y = 1¹/₂x. Функция эта выражает пропорциональную зависимость между у и х и потому графически изобразится, как мы знаем (§ 109), прямою, проходящею через начало координат и через точку М, у которой абсцисса есть 1, а ордината 1¹/₂.

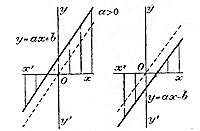
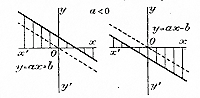
Если переменному числу х будем давать не только положительные значения, но и отрицательные, то прямая эта продолжится вниз, проходя через точку M', у которой абсцисса есть — 1 и ордината — 1¹/₂. Если теперь восстановим отброшенное прежде число + 2, т. е. возьмем функцию y = 1¹/₂x + 2, то увидим, что все ординаты этой функции будут более соответственных ординат функции y = 1¹/₂x на 2 единицы. Значит, график функции y = 1¹/₂x + 2 мы получим из графика функции y = 1¹/₂x если прямую линию MM' перенесем параллельно самой себе вверх на 2 единицы. Для этого отложим на оси Оу отрезок OA = 2 и через точку А проведем прямую, параллельную MM'. Эта прямая и будет служить графиком функции y = 1¹/₂x + 2. Абсцисса OD точки, в которой эта прямая пересекается с осью х-ов, равна корню двучлена, так как при этой абсциссе ордината у (т.е. величина самого двучлена) равна нулю (на нашем чертеже OD = —1¹/₃ ). Если возьмем функцию

то отрезок ОА пришлось бы отложить вниз от точки О, так как тогда все ординаты функции y = 1¹/₂x пришлооь бы уменьшить на 2 единицы. Мы получили бы тогда прямую
А'В', параллельную ММ' и отсекающую от оси у-ов отрезок ОА' = — 2. Корень этого двучлена равен абсциссе ОЕ точки, в которой прямая А'В' пересекается с осью x-ов (на чертеже OE = +1¹/₃).

Если в функции у = ах + b коэффициент а будет число отрицательное
(например y = —1¹/₂x + 2), то вспомогательная прямая, выражающая график функции
y = —1¹/₂x, пройдет через углы х'Оу и xOy', сообразно чему изменится и направление прямой ВС.

Таким образом, график двучлена у = ах + b есть прямая линия, параллельная прямой, выражающей функцию у = ах, и отсекающая от оси у - ов отрезок, равный b.

Вследствие того, что график функции у = ах + b есть прямая линия, сама эта функция называется линейной.

Для краткости речи в дальнейшем изложении вместо того, чтобы говорить: „прямая, выражающая функцию у = ах + b", мы будем говорить короче: „прямая у = ах + b".

Угол, образуемый прямою у = ах + b с осью x-ов, равен, конечно, углу, составляемому с осью x-ов прямою у = ах; следовательно, этот угол зависит только от величины коэффициента а, и поэтому коэффициент этот и в общем виде двучлена ах + b называется угловым.

Число b в двучлене ах + b есть так называемая начальная ордината, соответствующая начальному значению х = 0; она представляет собою отрезок оси y -ов, отсекаемый прямой, выражающей двучлен.

Коэффициент, как мы видели (§ 111), равен тангенсу угла, образованного с положительным направлением оси x-ов прямою у = ах (и, следовательно, параллельною ей прямою
у = ах + b ).

116. Изменение двучлена у = ах + b с изменением х. Прямая у = ах, параллельно которой проводится прямая у = ах + b, проходит через углы хОу и х'Оу' если а > 0, и через углы х'Оу и хОу', если а <0 (§§ 109, 110).

Следовательно, в первом случае прямая у = ах + b, если рассматривать ее в направлении слева направо,

подымается вверх,

черт. а

а во втором случае она опускается вниз

черт. b

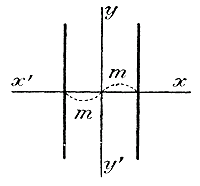
Если примем во внимание, что отрицательные числа тем больше, чем меньше их абсолютные величины, то мы можем скаэать, что при возрастании абсцисcы х (например, когда х переходит через ряд значений: ... — 4, — 3, —2,— 1, 0,1, 2, 3, 4...) ординаты возрастают, если а > 0 (черт.а), и убывают, если а < 0 (черт. b), причем это возрастание или убывание безгранично (конечно, если представлять себе прямые продолженными в обе стороны бесконечно) и притом равномерно, т. е. с увеличением х на одно и то же число (положим, на m) функция возрастает или убывает также на одно и то же число (положим, на n).

117. Замечания. I. Если угловой коэффициент а равен нулю, тогда двучлен обращается в одночлен у = b.

Это значит, что в графическом изображении должна получиться такая прямая, у которой все точки имеют одну и ту же ординату, равную b, а абсцисса может быть какая угодно. Такая линия, очевидно, есть прямая, параллельная оси х-ов и отсекающая от оси у-ов отрезок, равный b. Значит, при b положительном эта прямая расположится над осью х-ов, а при b отрицательном — под нею ; и в том и в другом случае при изменении х функция остается постоянной (равной b).

В частности, если при а = 0 еще и b = 0, т. е. если линейная функция будет y = 0, то график функции будет ось x-ов (для всякой точки этой оси ордината y = 0, а абсцисса произвольная).

II. Если какая-нибудь прямая параллельна оси у-ов , то тогда ординаты точек этой прямой могут иметь произвольные значения, абсциссы же для всех точек одинаковы, а именно: равны положительному или отрицательному отрезку m, который отсекается прямою от оси x-ов.

Следовательно, такую прямую можно выразить уравнением так: х = m (ордината у, не входящая в уравнение, остается произвольной). В частности, если m = 0, то получается уравнение х = 0, выражающее, что абсцисса всякой точки есть 0, а ордината какая угодно. Такая прямая есть ось у-ов.

118. Построение прямой у = ах + b по двум точкам. Чтобы построить прямую у = ах + b, можно было бы сначала построить вспомогательную прямую, выражающую функцию у = ах, и потом провести параллельную прямую, отсекающую от оси у-ов отрезок b. Но проще построить прямую у = ах + b, найдя предваритeльно какие-нибудь две точки этой прямой. Положим, например, надо построить прямую:

Для этого найдем координаты каких-нибудь двух точек, принадлежащих искомой прямой, например, координаты тех точек, в которых прямая пересекается с осями координат. Для нахождения их положим в данном уравнении х = 0 и определим соответствующее значение у, а затем положим у = 0 и определим х; тогда найдем:

Точка с абсциссой 0 и ординатой 3 есть точка Р (черт. 32); точка с абсциссой 6 и ординатой 0 есть Q значит, искомый график будет прямая PQ, проходящая через эти две точки.

Если точки пересечения с координатными осями (или одна из них) не помещаются в пределах чертежа, то можно подыскать другие точки, которые помещались бы на чертеже.

Замечание. Для уменьшения погрешности при черчении прямой желательно, чтобы две точки, через которые проводится прямая, отстояли друг от друга по возможности дальше, тогда некоторая неточность в положении линейки (избегнуть которую очень трудно) не так много отразится на направлении проводимой прямой.

119. Графическое решение уравнения. Пусть требуется решить графическим путем уравнение:

Способ 1-й. Перенеся все члены в левую часть, сделаем приведение подобных членов:

В таком виде уравнением требуется найти такое значение числа х, при котором двучлен 2х — 5 обращается в нуль; другими словами, требуется найти корень этого двучлена. Для этого, как мы видели, достаточно построить график двучлена и найти на чертеже величину абсциссы той точки, в которой график пересекается с осью x-ов. График двучлена

есть прямая линия, которую мы можем построить по двум точкам, например таким:

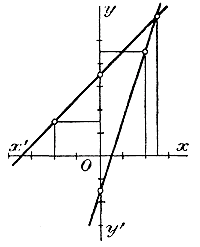
На чертеже мы получили прямую, которая пересекается о осью x-ов в точке c абсциссой + 2¹/₂; это и будет корень уравнения 2х — 5 = 0.

Способ 2-й. Части данного уравнения, взятые отдельно, представляют собою два двучлена:

Уравнение требует найти такое значение числа х, при котором оба двучлена имели бы одинаковую численную величину. Для нахождения такого значения построим на одном и том же чертеже графики обоих двучленов, например по таким точкам:

Две построенные по этим точкам прямые пересекаются в точке, абсцисса которой составляет + 2¹/₂;. Это и будет корень данного уравнения, так как при х = + 2¹/₂; ординаты y₁ и y₂ равны между собою и, следовательно,

3x —1,5 = x + 3,5.

Замечание. Графический способ решения уравнений первой степени не представляет каких-либо преимуществ с алгебраическим приемом решения, так как такие уравнения решаются весьма просто и без графиков. Но для решения уравнений более сложных графический метод иногда бывает весьма полезен (впоследствии мы увидим этому примеры).