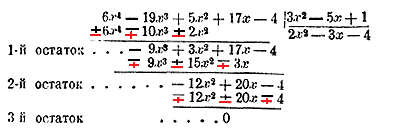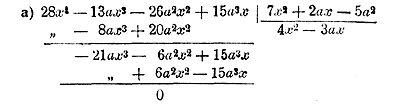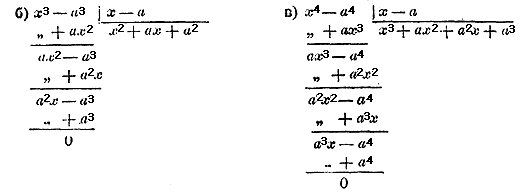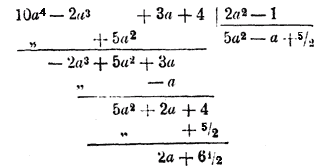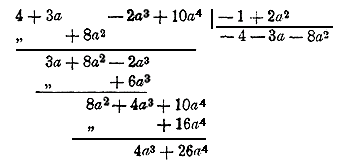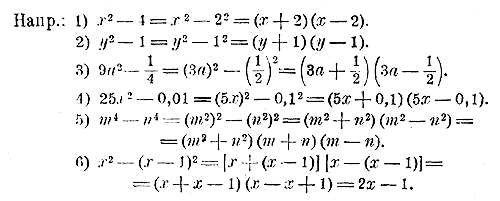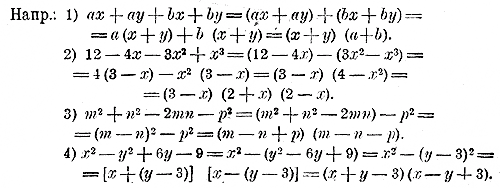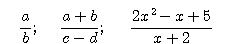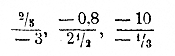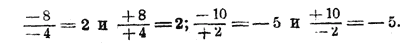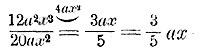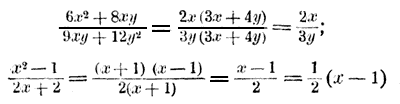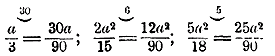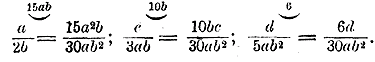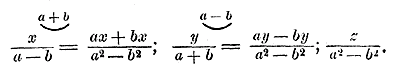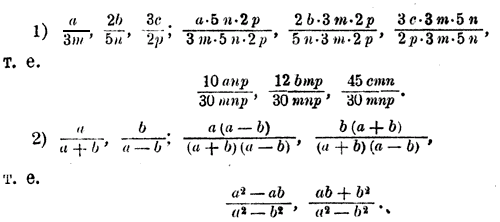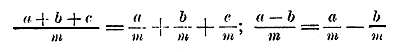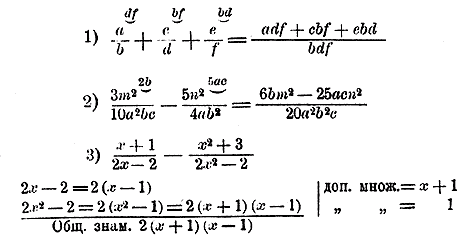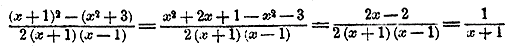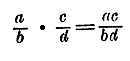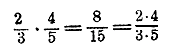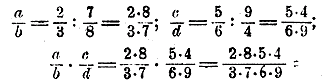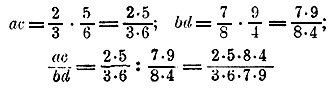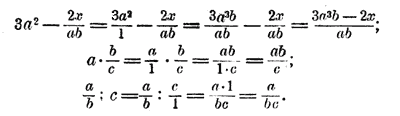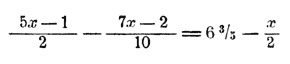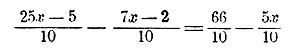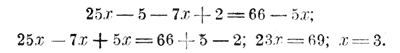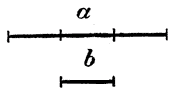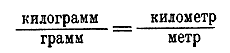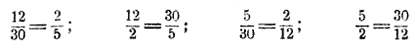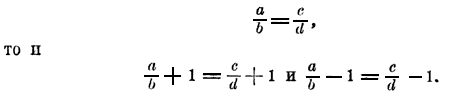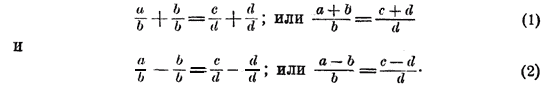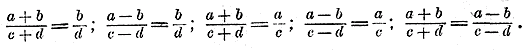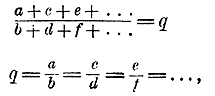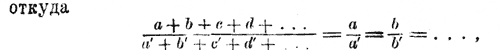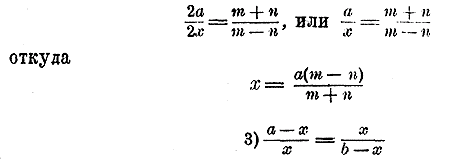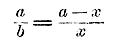| АЛГЕБРА В НАЧАЛО |
|
ОТДЕЛ ВТОРОЙ. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ (ПЕРВЫЕ ЧЕТЫРЕ АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ). Глава первая. Многочлен и одночлен. Многочлен и одночлен. 42. Многочлен и одночлен. Алгебраическое выражение, составленное из нескольких других выражений, соединенных между собою знаками + или —, называется многочленом. Таково, напр., выражение:
Отдельные выражения, от соединения которых знаками + или — получился многочлен, называются его членами. Обыкновенно члены многочлена рассматриваются вместе с теми знаками, которые стоят перед ними; напр., говорят: член — а, член + b2 и т. п. Перед первым членом, если перед ним не поставлено никакого знака, можно подразумевать энак + ; так, в нашем примере первый член есть аb или + аb. Выражение, состоящее только из одного члена, называется одночленом, из двух членов —двучленом, из трех — трехчленом и т. п. Одночлен представляет собой или отдельное число, выраженное буквой или цифрами (напр. — а, + 10), или произведение (напр. аb), или частное (напр. а-b/2 ) или степень (напр. b2); но одночлен не должен представлять собою ни сумму, ни разность, так как в противном случае это был бы двучлен, трехчлен, вообще многочлен. Если одночлен представляет собою частное, то он называется дробным одночленом; все другие одночлены называются ц е л ы м и. Так, в нашем примере одночлен а-b/2 есть дробный, а все остальные члены многочлена целые. Так как в начале алгебры мы будем говорить только о целых одночленах, то для краткости мы будем их называть просто „одночленами". Если все члены многочлена целые, то он также называется ц е л ы м. 43. Коэффициент. Положим, дано произведение: a 3ab (— 2), в котором некоторые сомножители выражены цифрами, другие— буквами. Такие произведения можно преобразовать (пользуясь сочетательным и переместительным свойствами умножения), соединив в одну группу все сомножители, выраженные цифрами, в другую группу - все сомножители, выраженные буквою а, и т. д.: 3 (— 2) (аа)b, что можно написать короче: — 6a2b;. Подобно этому: — l0 axx ( — 2) = + 20ах2, и т. п. Выраженный цифрами сомножитель, поставленный впереди буквенных сомножителей, называется коэффициентом одночлена. Так, в одночлене — 6a2b число — 6 есть коэффициент 1). Заметим, что если коэффициент есть целое положительное число, то он означает, сколько раз повторяется слагаемым то буквенное выражение, к которому он относится; так, 3ab = 3(ab) =(ab)•3=ab + ab + ab. Если коэффициент есть дробь, то он выражает, какая дробь берется от численной величины буквенного выражения. Так: 44. Свойства многочлена. Всякий многочлен можно рассматривать как алгебраическую сумму его членов. Напр., многочлен 2а — b + с есть сумма: 2а + (— b) + (+ с ) так как выражение + (— b) равносильно выражению — b и выражение + (+ с ) означает то же, что и + с. Вследствие этого все свойства суммы относительных чисел (отдел1§ 25) принадлежат также и многочлену. Напомним главнейшие из этих свойств: а) Переместительное свойство: численная величина многочлена не изменяется при перемещении его членов (с их знаками). Положим, напр., мы находим численную величину многочлена 2а2 — аb + b2 — 1/2 а при а = — 4 и b = — 3. Для этого предварительно вычислим каждый член отдельно: 2а2 = 2(— 4)2 = 2(— 4)(— 4) = 32; — аb = — (— 4) (— 3)= —12; b2 =(— 3)2 = (— 3)(— 3)= +9; — 1/2 а = — 1/2 (— 4)= +2. Теперь сложим все полученные числа или в той последовательности, в какой написаны члены многочлена: 32 — 12 + 9 + 2 = 31, или в каком-нибудь ином порядке,— всегда получим одно и то же число 31. б) Сочетательное свойство: численная величина многочлена не изменится, если какие-либо его члены мы заменим их алгебраической суммой. Так, если во взятом сейчас многочлене мы заменим члены — аb, + b2 и — 1/2 а их алгебраической суммою, т. е. возьмем этот многочлен в таком виде: 2а2 + (— аb + b2 — 1/2 а ) то при а = — 4 и b = — 3 получим: 32 + (— 12 + 9 + 2) = 32 + (— 1) = 31, т. е. получим то же самое число 31, которое получили прежде. Заметим еще следующее важное свойство многочлена: в) Если перед каждым членом многочлена переменим знак на , противоположный, то численная величина многочлена изменит также знак на противоположный, а абсолютная величина ее не изменится. Напр., численная величина многочлена 2а2 — аb + b2 — 1/2 а 45. Приведение подобных членов. Иногда в многочлене вcтречаются такие члены, которые отличаются друг от друга только коэффициентами, или знаками, или даже и совсем не отличаются; такие члены называются подобными. Напр., в многочлене
первый член подобен третьему (они подчеркнуты одной чертой), второй член подобен четвертому и шестому (подчеркнуты двумя чертами), а пятый член не имеет себе подобных. Если в многочлене встречаются подобные между собой члены, то их можно соединить в один член. Так, в приведенном сейчас примере мы можем (основываясь на сочетательном свойстве многочлена) соединить члены в такие группы: (4а + 0,5a) + (— 3x + 8x — 2х) + 3ax. Но очевидно, чго 4 каких-нибудь числа да 0,5 такого же числа составляют 4,5 этого же числа. Значит, 4а + 0,5a = 4,5a. Равным образом — 3x + 8x = 5х и 5х — 2х =3х. Значит, многочлен можно изобразить так: 4,5a + 3х + 3ax. Заметим, что соединение всех подобных между собою членов многочлена в один член принято называть приведением подобных членов многочлена. Замечание. Два подобных члена о одинаковыми коэффициентами, но о разными (знаками взаимно уничтожаются, таковы, напр., члены + 2а и —2а, или —1/2 х2 и +1/2 х2. Примеры.
Алгебраическое сложение и вычитание. 46. Что представляют собою „алгебраические действия". В арифметике действия производятся над числами, и в результате получается одно новое число. В алгебре действия производятся не над числами, а над алгебраическими выражениями, и в результате получается новое алгебраическое выражение. Напр., умножить одночлен 3a на одночлен 2а — значит, во-первых, указать умножение принятыми знаками: (3а) (2а) и, во-вторых, преобразовать, если возможно, полученное алгебраическое выражение в другое, более простое. В нашем примере преобразование можно выполнить, рассуждая так: чтобы умножить какое-нибудь число на произведение 2 • а, можно умножить это число сначала на 2, а потом результат умножить на а. Значит: (3а) (2а) = (3а) 2а. В последнем выражении мы можем скобки отбросить, так как от этого смысл выражения не изменяется; тогда получим 3а 2а.. Теперь, пользуясь сочетательным свойством умножения, сгруппируем сомножители так: (3 • 2) (аа), что, очевидно, составляет 6а2. Какое бы число буква а ни означала, численная величина выражения (3а) (2а) всегда равна численной величине выражения 6а2, т. е. эти выражения тождественны. Таким образом, алгебраическое действие в нашем примере умножения состоит, во-первых, в указании этого действия принятыми в алгебре знаками и, во-вторых, в преобразовании, если возможно, полученного алгебраического выражения в другое, тождественное ему. 47. Сложение одночленов. Пусть требуется сложить несколько одночленов: 3а, — 5b, + 0,2а, — 7b и с. Их сумма выразится так: 3а + ( — 5b) + (+ 0,2а) + ( — 7b) + с Но выражения: + ( — 5b), + (+ 0,2а) и + ( — 7b) равносильны выражениям: — 5b, + 0,2а и — 7b поэтому сумму данных одночленов можно переписать проще так:
что после приведения подобных членов даст: 3,2а — 12b + с. Значит, чтобы сложить несколько одночленов, достаточно написать их один за другим с их знаками и сделать приведение подобных членов. 48. Сложение многочленов. Пусть требуется к какому-нибудь числу или алгебраическому выражению m прибавить многочлен а — b + с. Искомую сумму можно выразить так: m + (а — b + с). Чтобы преобразовать это выражение, примем во внимание, что многочлен m + (а — b + с) = m + а + (— b ) + с Но прибавить — b все равно, что вычесть b; поэтому: m + (а — b + с) = m + а — b + с Правило. Чтобы к какому-нибудь альебраическому выражению прибавить многочлен, надо приписать к этому выражению все члены многочлена один за другим с их знаками (причем перед первым членом многочлена, если перед ним не стоит никакого знака, надо подразумевать знак +) и сделать приведение подобных членов, если они окажутся. Пример. 3а2 — 5ab + b2 + (4ab — b2 + 7a2). Первое слагаемое, которое мы обозначали сейчас одной буквой m, дано в этом примере в виде многочлена 3а2 — 5ab + b2 . Применяя указанное правило, найдем: 3а2 — 5ab + b2 + (4ab — b2 + 7a2) = 3а2 — 5ab + b2 + 4ab — b2 + 7a2 = 10а2 — ab Если данные для сложения многочлены содержат подобные члены (как в нашем примере), то слагаемые полезно писать одно под другим так, чтобы подобные члены стояли под подобными:
49. Вычитание одночленов. Пусть требуется из одночлена 10ax вычесть одночлен —3ax. Искомая разность выразится так: 10ax — (— 3ax). Согласно правилу вычитания, вычитание — 3ax можно заменить прибавлением числа, противоположного числу — 3ax. Такое число ecть + 3ax, поэтому: 10ax — (— 3ax) = 10ax + (+ 3ax) = 10ax + 3ax = 13ax. Значит, чтобы вычесть одночлен, достаточно приписать его к уменьшаемому с противоположным знаком (и сделать приведение подобных членов, если они окажутся). 50. Вычитание многочленов. Пусть требуется из какого-нибудь числа или алгебраического выражения m вычесть многочлен а — b + с, что можно обозначить так: m — (а — b + с). Для этого, согласно правилу вычитания (Отдел1§ 22), достаточно прибавить к m число, противоположное числу а — b + с. Такое число есть — а + b — с (§ 44, в); значит: m — (а — b + с) = m + (— а + b — с) Применяя теперь правило сложения многочленов, получим: m — (а — b + с) = m — а + b — с. Значит, чтобы из какого-нибудь алгебраического выражения вычесть многочлен, достаточно к этому выражению приписать все члены вычитаемого многочлена с противоположными знаками (и сделать приведение). Если требуется вычесть из одного многочлена другой многочлен и в этиx многочленах имеются подобные члены, то вычитаемый многочлен полезно писать под уменьшаемым, переменяя знаки у вычитаемого многочлена на противоположные, и так, чтобы подобные члены стояли под подобными. Напр., вычитание
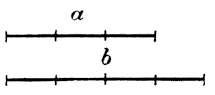
(в вычитаемом многочлене верхние знаки поставлены те, какие были заданы, а внизу они переменены на противоположные). 51. Раскрытие скобок, перед которыми стоит знак + или—. Пусть в выражении 2а + (а —3b + с) — (2а — b + 2с) требуется раскрыть скобки. Это надо понимать так, что требуется над многочленами, стоящими внутри скобок, произвести те действия, которые указаны знаками, стоящими перед скобками. В нашем примере перед первыми скобками стоит знак +, перед вторыми знак—. Произведя сложение и вычитание по данным нами правилам, получим выражение без скобок: 2а + а —3b + с — 2а + b — 2с = а — 2 b — с Таким образом, мы должны помнить, что, раскрывая скобки, перед которыми стоит знак +, мы не должны изменять знаки внутри скобок, а раскрывая скобки, перед которыми стоит знак —, мы должны перед всеми членами, стоящими внутри скобок, переменить знаки на противоположные. Пусть еще требуется раскрыть скобки в выражении: 10р — [3p + (5p — 10) — 4]. Для этого всего удобнее раскрыть сначала внутренние скобки, а потом внешние: 10р — [3p + 5p — 10 — 4] = 10р — 3p — 5p + 10 + 4] = 2p + 14. 52. Заключение в скобки части многочлена. Для преобразования многочлена иногда бывает полезно заключить в скобки совокупность некоторых его членов, причем перед скобками иногда желательно поставить + т. е. изобразить многочлен в виде суммы, а иногда знак —, т.е. изобразить многочлен в виде разности. Пусть, напр., в многочлене а + b — с мы желаем заключить в скобки два последних члена, поставив перед скобками знак +. Тогда пишем так: а + b — с = а +( b — с), т. е. внутри скобок оставляем те же знаки, какие были в данном многочлене. Что такое преобразование верно, убедимся, если раскроем скобки по правилу сложения; тогда получим снова данный многочлен. Пусть в том же многочлене требуется заключить в скобки два последние числа, поcтавив перед скобками знак минус. Тогда напишем так: а + b — с = а — ( — b + с) = а — ( с — b ), т. е. внутри скобок перед всеми членами переменяем знаки на противоположные. Что такое преобразование верно, убедимся, если раскроем скобки по правилу вычитания; тогда получим снова данный многочлен. Замечание. Можно и весь многочлен заключить в скобки, поставив перед ними знак + или —. Напр., можно написать: а — b + с = + (а — b + с) и а — b + с = — (— а + b — с). Алгебраическое умножение. 53. Умножение степеней одного и того же числа. Пусть надо умножить а3 на а2, что можно обозначить так: а3а2, или подробнее: (ааа) (аа). Здесь произведение ааа умножается на другое произведение аа. Но чтобы умножить какое-нибудь число на произведение, можно умножить это число на первый сомножитель, полученный результат умножить на второй сомножп тель, и т. д.; поэтому: а3а2 = (ааа)(аа) = (ааа) аа, что может быть написано и без скобок, так как порядок действий остается и без скобок такой же, какой указан скобками: а3а2 = ааааа = а5. Значит, при умножении степеней одного и того же числа показатели их складываются. Таким образом: х3х = х4, m2m3 = m5, y2 y y3 = y6, и т. д. 54. Умножение одночленов. Мы уже говорили раньше (§ 46), как можно преобразовать произведение одночленов (3а) (2а) в одночлен 6а2. Повторим теперь сказанное тогда на другом примере. Пусть дано умножить: 3ах2(— 5аbх) 2). Так как одночлен — 5аbх есть произведение, то достаточно умножить множимое на первый сомножитель —5, результат умножить на второй сомножитель а, и т. д. Значит: 3ах2(— 5аbх) = 3ах2(— 5)аbх. В этом произведении, пользуясь сочетательным свойством умножения, сгруппируем сомножители в такие группы: (+3)(— 5) (аа) b (х2х). Произведя умножение в каждой группе, получим: — 15 a2b х3. Значит, чтобы умножить одночлен на одночлен, надо перемножить их коэффициенты, сложить показатели одинаковых букв, а те буквы, которые входят только во множимое или только во множитель, перенести в произведение с их показателями. Примеры. 1) 0,7a3х (3a4х2у2) = 2,1a7х3у2 2) ( 1/2 m х3 )2 = 1/2 m х3 ( 1/2 m х3 ) = 1/4 m2 х6 3) —3,5 х2у ( 3/4 х3) = — 21/8 х5у 55. Умножение многочлена на одночлен. Пусть дано умножить многочлен а + b — с на одночлен m, что можно выразить так: (а + b — с) m. Многочлен а + b — с есть сумма относительных чисел а + b + (— с). Но, чтобы умножить сумму, можно умножить каждое слагаемое отдельно и результаты сложить (распределительное свойство); значит: (а + b — с) m = [ а + b + (— с) ] m = аm + bm + (— с)m . Но (— с)m = — cm и + (—cm) = — cm; поэтому (а + b — с) m = аm + bm — сm. Правило. Чтобы умножить многочлен на одночлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить. Так как произведение не изменяется от перестановки мест сомножителей, то это правило применимо также и к умножению одночлена на многочлен; таким образом: m(а + b — с) = mа + mbm— mс. Примеры. 1) (3x2 — 2ах + 5а2) (—4ах). Здесь умножение членов многочлена на данный одночлен надо производить по правилу умножения одночленов, принимая во внимание также и правило знаков: одинаковые знаки при умножении дают +, а разные знаки дают —. Умножаем отдельно каждый член многочлена на одночлен: (3x2)(—4ах) = — 12аx3; (— 2ах) (—4ах) == + 8а2x2; (+ 5а2) (—4ах) = — 20а3x . Теперь сложим полученные результаты: — 12аx3 + 8а2x2 — 20а3x. 2) (а2 — ab + b2) (3а) = а2 (3а) — (ab) (3а) + b2 (3а) = 3а3 — 3а2b + 3ab2 3) ( 7x3 + 3/4 ах — 0,3) (2,l а2x) = (7x3) (2,l а2x) + ( 3/4 ах ) (2,l а2x) — 0,3 (2,l а2x) = 4) 2а (3а — 4 ах + 1/2 x2) = 6а2 — 8а2x + аx2 56. Умножение многочлена на многочлен. Пусть требуется произвести умножение: (а + b — с) (m — n). Рассматривая множитель m — n как одно число (как одночлен), применим правило умножения многочлена на одночлен: а (m — n) + b (m — n) — с (m — n). Рассматривая теперь выражение m — n как многочлен (двучлен), применим правило умножения одночлена на многочлен: (am — an) + (bm — bn) — (cm — cn). Наконец, раскрыв скобки по правилам сложения и вычитания, окончательно найдем: (а + b — с) (m — n) = am — an + bm — bn — cm + cn Правило. Чтобы умножить многочлен на многочлен, надо умножить каждый член первого многочлена на каждый член второго многочлена и полученные произведения сложить. Конечно, при умножении членов первого многочлена на члены второго многочлена нужно руководствоваться правилами знаков: одинаковые знаки дают + разные знаки —. Пример, (а2 — 5аb + b2 — 3) (а3 — 3аb2 + b3 ) Умножим сначала все члены множимого на 1-й член множителя: (а2 — 5аb + b2 — 3) а3 = а5 — 5а4b + а3b2 — 3а3 Затем умножим все члены множимого на 2-й член множителя: (а2 — 5аb + b2 — 3) ( — 3аb2) = — 3а3b2 + 15а2b3 — 3аb4 + 9аb2 Далее, умножим на третий член множителя: (а2 — 5аb + b2 — 3) (b3 ) = а2b3 — 5аb4 + b5 — 3b3 Наконец, сложим все полученные произведения и сделаем приведение подобных членов; окончательный результат будет: а5 — 5а4b — 2а3b2 — 3а3 + 16а2b3 — 8аb4 + 9аb2 + b5 — 3b3 Замечания. 1) Чтобы при умножении многочлена на многочлен не пропустить ни одного из произведений членов, полезно всегда держаться какого-нибудь одного порядка yмножения; напр., как это мы сейчас делали, умножить сначала все члены множимого на 1-й член множителя, затем умножить все члены на 2-й член множителя, и т. д. 2) В применении к арифметическим числам правило умножения многочленов может быть наглядно истолковано геометрически. Возьмем, напр., 4 отрезка прямой а, b, m и n и построим два прямоугольника: один с основанием а + b и высотою m + n, другой с основанием а + b ,и высотою m — n.
Площадь первого равна (а + b) (m + n), а площадь второго будет (а + b) (m — n). Из чертежей непосредственно видно, что первая площадь равна am + bm + an + bn, а вторая равна am + bm — an — bn. Примеры. 1) (а — b) (m — n — р) = am — bm — an + bn — аp + bр. 2) (x2 — у2) (x + у) = x3 — xу2 + x2 у — у3 3) (3аn + 2n2 — 4a2) (n2 — 5an) = 3аn3 + 2n4 — 4a2n2 — 15a2n2 — 10an3 + 20a3n = 4) (2a2 — 3)2 = (2a2 — 3) (2a2 — 3) = (2a2)2 — 3 (2a2) — (2a2) 3 + 9 = 57. Расположенный многочлен. Расположить многочлен по степеням какой-нибудь буквы — значит, если возможно, написать его члены в такой последовательности, чтобы показатели этой буквы увеличивались или уменьшались от первого члена к последнему. Так, многочлен 1 + 2х + x2 — x3 расположен по в о з р астающим степеням буквы х. Тот же многочлен будет расположен по убывающим степеням буквы х, если члены его напишем в обратном порядке: — x3+ x2 + 2х +1. Буква, по которой расположен многочлен, называется главной его буквой. Член, содержащий главную букву с наибольшим показателем, называется высшим членом многочлена; член, содержащий главную букву с наименьшим показателем или не содержащий ее вовсе, называется низшим членом многочлена. 58. Умножение расположенных многочленов всего удобнее производить так, как будет указано на следующем примере. Умножить 3х — 5 + 7x2 — x3 на 2 — 8x2 + х. Расположив оба многочлена по убывающим степеням буквы х, пишут множитель под множимым и под ними проводят черту:
Умножают все члены множимого на 1-й член множителя (на — 8x2) и полученное произведение пишут под чертою. Умножают затем все члены множимого на 2-й член множителя (на + х) и полученное второе произведение пишут под первым так, чтобы подобные члены стояли под подобными. Также поступают и далее. Под последним произведением (на + 2) проводят черту, под которою пишут полное произведение, складывая все остальные произведения. Можно также оба многочлена расположить по возрастающим степеням главной буквы и затем производить умножение в том порядке, как было сейчас указано. 59. Высший и низший члены произведения. Из рассмотрения этих примеров следует: Высший член произведения равен произведению высшего члена множимого на высший член множителя. Низший член произведения равен произведению низшего члена множимого на низший член множителя. Остальные члены произведения могут получиться от соединения нескольких подобных членов в один. Может даже случиться, что в произведении, после приведения подобных членов, все члены уничтожатся, кроме первого и последнего (высшего и низшего), как это видно на следующем примере:
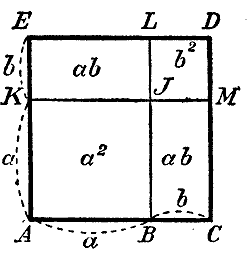
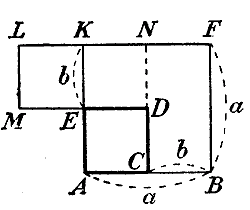
60. Число членов произведения. Пусть во множимом будет пять членов, а во множителе три члена. Умножив каждый член множимого на 1-й член множителя, мы получим 5 членов произведения; умножив затем каждый член множимого на 2-й член множителя, мы получим еще б членов произведения и т. д.; значит, всех членов в произведении окажется 5•3, т. е. 15. Вообще, число членов произведения, до соединения в нем подобных членов, равно произведению числа членов множимого на число членов множителя. Так как высший и низший члены произведения не могут иметь себе подобных членов, а все прочие члены могут уничтожиться, то наименьшее число членов произведения после приведения в нем подобных членов равно 2. 61. Некоторые формулы умножения двучленов. Полезно запомнить следующие формулы умножения двучленов: а) (а + b)2 = (а + b) (а + b) = a2 + аb + аb + b2 = a2 + 2аb + b2. Напр.: 172 = (10 + 7)2 = 102 + 2 • 10 • 7 + 72 = 100 + 140 + 49 = 289. Таким образом, квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа. б) (а — b)2 = (а — b) (а — b) = a2 — аb — аb + b2 = a2 — 2аb + b2. Напр.: 192 = (20 —1)2 = 202 — 2 • 20 • 1 + 12 = 400 — 40 + 1 = 361 Таким образом, квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа. Замечание. Полезно заметить, что возвышение в степень по отношению к сложению и вычитанию не обладает распределительным свойством; так, (2+3)2 не равно в) (а + b) (а — b) = a2 + аb — аb — b2 = a2 — b2 Напр.: 25 • 15 = (20 + 5) (20 — 5) = 202— 52 = 400 — 25 = 375. Таким образом, произведение суммы двух чисел на их разность равно разности квадратов этих чисел. г) (а + b)3 = (а + b)2 (а + b) = (a2 + 2аb + b2)(а + b) = Напр.: 123 = (10 + 2)3= 103 + 3•102•2 + 3•10•22 + 23 = 1000 + 600 + 120 + 8=1728. Таким образом, куб суммы, двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведенне первого числа на квадрат второго, плюс куб второго числа. д) (а — b)3 = (а — b)2 (а — b) = (a2 — 2аb + b2)(а — b) = Напр.:193 = (20 — 1)3 = 203 — 3•202•1 + 3•20•12 — 13 = 8000 —1200 + 60 — 1= 6869. Таким образом, куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведенне первого числа па квадрат второго, минус куб второго числа. 62. Геометрическое истолкование некоторых из этих формул. а) Отложим отрезок прямой АВ = а и к нему приложим отрезок ВС = b , затем построим квадраты: ACDE и ABJK, которых площади будут равны (а + b)2 и а2 . Продолжив прямые BJ н KJ до пересечения с ED и CD, мы разобьем больший квадрат на 4 части, которых площади будут: а2, b2, ab и ab.
Значит: (а + b)2 = a2 + аb + аb + b2 = a2 + 2аb + b2. б) Отложим АВ = a и из AВ вычтем ВС=b; затем построим квадраты ACDE, ABFK и KLME, которых площади будут (а — b)2 , а2 и b2. Продолжив CD до точки N, мы получим: пл. ACDE = пл. AВFK + пл. EKLM— пл. CBFN — пл. DNLM.
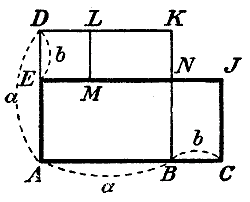
Значит: (а — b)2 = a2+ b2— аb — аb = a2 — 2аb + b2. в) Отложив (черт. 13) АВ = а, BG = b, AD = a и DE = b, построим прямоугольник ACJE и квадраты ABKD и DEML.
Тогда пл. ACJE = пл. ABKD + пл. BCJN — пл. DEML — пл. LMNK. Но прямоугольники BCJN и LMNK равны, и потому их площади в написанном нами равенстве взаимно уничтожаются: пл. ACJE = пл. ABKD — пл. DEML, т. е. (а + b)(а—b) = а2 — b2. 63. Применения. При помощи указанных формул можно иногда производить умножение многочленов проще, чем обыкновенным путем. Приведем примеры: 1) (4а3 — 1)2 = (4а3 )2 — 2 (4а3)• 1 +12 = 16а6 — 8a3 + 1 2) (х + y)(y — х) = (у + х)(у — х) = у2 — х2. 3) (х + у + 1)(х — у +1) = [(х + 1) + у] [(х +1) — у] = (х +1)2 — у2 = х2 + 2x +1 — у2. 4) (а — b + с)(а + b — с)=[а — (b— с)] [а + (b — с)] = = а2 — (b — с)2 = а2 — (b2 — 2bс + с2) = а2 — b2 + 2bс — с2
Алгебраическое деление. 64. Деление степеней одного и того же числа. Пусть требуется разделить: а 5: а 2. Так как делимое должно равняться делителю, умноженному на частное, а при умножении показатели одинаковых букв складываются, то в искомом частном показатель буквы а должен быть такое число, которое, сложенное с 2, составляет 5; такое число равно разности 5 — 2. Значит: а 5: а 2= а 5-2= а 3 Подобно этому найдем: x3: х2 = х ; у4: у = у3 и т. п. Значит, при делении степеней одного и того же числа показатель делителя вычитается из показателя делимого.Если только число, степени которого делятся, не равно нулю. Так, нельзя написать: 0m: 0n = 0m-n, так как это равенство означало бы: 0:0 = 0, тогда как частное 0:0 может равняться любому числу 65. Нулевой показатель. Если при делении степеней одного и того же числа показатель делителя окажется равным показателю делимого, то частное должно равняться 1; напр.: а3: а3 = 1, потому что а3= а3•1. Условимся производить вычитание показателей и в этом случае; тогда в частном мы получим букву с нулевым показателем: 66. Деление одночленов. Пусть дано разделить: (12а3b2х) : (4а2b2). Впрочем, ради краткости писания скобки в подобных обозначениях принято опускать. Согласно определению деления, частное, будучи умножено на делитель, должно составить делимое. Поэтому у искомого частного коэффициент должен быть 12 : 4, т. е. 3; показатель у буквы а получится вычитанием из показателя этой буквы в делимом показателя той же буквы в делителе, буква b совсем не войдет в частное, или—что все равно—войдет в него с показателем 0, а буква х перейдет в частное со своим показателем. Таким образом: 12а3b2х : 4а2b2 = 3ах. Поверка: 3ах • 4а2b2= 12а3b2х Правило. Чтобы разделить одночлен на одночлен, надо коэффициент делимого разделить на коэффициент делителя, из показателей букв делимого вычесть показатели тех же букв делителя и перенести в частное, без изменения показателей, те буквы делимого, которых нет в делителе. Примеры. 1) 3m3n4x : 4m2nx = 3/4 m n3 2) — ax4y3: — 5/6 axy2 = + 6/5x3у. 3) 0,8axn : — 0,02ax = — 40xn-1. 67. Признаки невозможности деления одночленов. Если частное от деления целых одночленов не может быть выражено точно целым одночленом, то говорят,что такое деление невозможно. Деление одночленов невозможно в двух олучаях: а) Когда в делителе есть буквы, которых нет в делимом. Напр., нельзя разделить 4аb2 на 2ах, так как всякий одночлен, умноженный на 2ах дает произведение, содержащее букву х, а в нашем делимом такой буквы совсем нет. б) Когда показатель какой-либо буквы в делителе больше показателя той же буквы в делимом. Напр., деление 10а3b2 : 5аb3 невозможно, так как всякий одночлен, умноженный на 5аb3, дает в произведении такой одночлен, который содержит букву b с показателем 3 или с показателем, большим 3, тогда как в нашем делимом эта буква стоит с показателем 2. Когда один одночлен не делится на другой одночлен, то частное может быть только указано посредством знаков деления; так частное от деления 4а2b : 2ас может быть указано или так: 4а2b : 2ас, или так: 68. Деление многочлена на одночлен. Пусть требуется разделить многочлен а + b — с на одночлен m, что можно выразить так: (а + b — с) : m, или Многочлен а + b — с есть алгебраическая сумма, а чтобы разделить алгебраическую сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно; поэтому:
В этом можно убедиться и поверкою: умножив многочлен a/m + b/m — c/m на делитель m, мы получим делимое а + b — с Правило. Чтобы разделить многочлен на одночлен, надо разделить на этот одночлен каждый член многочлена и полученные частные сложить. Конечно, деление членов многочлена на одночлен производят по правилу деления одночленов. Примеры.
69. Деление одночлена на многочлен. Пусть требуется одночлен а разделить на многочлен b+ с—d. Частное от такого деления не может быть выражено ни целым одночленом, ни целым многочленом, так как если допустим, что частное равно какому-нибудь целому одночлену или целому многочлену, то произведение этого частного на многочлен b+ с—d дало бы тоже многочлен, а не одночлен, как требуется делением. Частное от деления а на b+ с—d может быть только обозначено знаками деления: а : (b+ с—d), или 70. Деление многочлена на многочлен.Частное от деления многочлена на многочлен только в редких случаях можно виразить в виде целого многочлена. Напр.: (a2 + 2аb + b2) : (а + b) = а + b так как (а + b) (а + b) = (а + b)2 = a2 + 2аb + b2. Вообще же подобные частные можно только обозначить знаком деления. Напр., частное от деления а — b + с на d — e выразится так:
Выразить частное в виде целого многочлена иногда удастся тогда, когда оба многочлена расположены по степеням одной и той же буквы. Покажем, как это сделать, на следующем примере: (5x2 — 19x3 + 17x + 6x4 — 4) : (1 — 5х + Зх2). Напишем оба многочлена по убывающим степеням буквы х и расположим деление так, как оно располагается при делении целых чисел:
Предположим, что искомое частное равно какому-нибудь многочлену и что члены этого многочлена расположены тоже по убывающим степеням буквы х. Делимое должно равняться произведению делителя на частное. Из умножения расположенных многочленов известно (§ 58), что высший член произведения равен произведению высшего, члена множимого на высший член множителя. В делимом высший член есть первый, в делителе и частном высшие члены тоже первые. Значит, 1-й член делимого (6x4) должен быть произведением 1-го члена делителя (Зx2) на 1-й член частного. Отсюда следует: чтобы найти 1 й член частного, достаточно разделить 1-й член делимого на 1-й член делителя. Разделив, находим 1-й член частного 2x2. Пишем его под чертою в частном. Умножим все члены делителя на 1-й член частного и полученное произведение вычтем из делимого. Для этого напишем его под делимым так, чтобы подобные члены стояли под подобными, и у всех членов вычитаемого переменим знаки на обратные. Получим после вычитания 1-й остаток. Если бы этот остаток оказался равным нулю, то это значило бы, что в частном никаких других членов, кроме найденного 1-го, нет, т. е. что частное есть одночлен. Если же, как в нашем примере, 1-й остаток не есть нуль, то будем рассуждать так. Делимое есть произведение всех членов делителя на каждый член частного. Мы вычли из делимого произведение всех членов делителя на 1-й член частного; следовательно, в 1-м остатке заключается произведение всех членов делителя на 2-й, на 8-й и следующие члены частного. Высший член в остатке есть 1-й; высший член делителя тоже 1-й; высший член в частном (не считая 1-го) есть 2-й член. Значит, 1-й член остатка (—9x3) должен равняться произведению 1-го члена делителя на 2-й член частного. Отсюда заключаем: чтобы найти 2-й член частного, достаточно разделить 1-й член 1-го остатка на 1-й член делителя. Разделив, находим 2-й член частного — Зх. Пишем его в частном. Умножим на 2-й член частного все члены делителя и полученное произведение вычтем из 1-го остатка. Получим 2-й остаток. Если этот остаток равен нулю, то деление окончено; если же, как в нашем примере, 2-й остаток не равен нулю, то будем рассуждать так. 2-й остаток есть произведение всех членов делителя на 3-й, на 4-й и следующие члены частного. Так как из этих членов частного высший есть 3-й, то, подобно предыдущему, 3-й член частного найдем, если 1-й член 2-го остатка разделим на 1-й член делителя. Разделив, находим — 4. Умножив на —4 все члены делителя и вычтя произведение из остатка, получим 3-й остаток. В нашем примере этот остаток оказался нулем; это показывает, что в частном других членов, кроме найденных, не может быть. Если бы 3-й остаток был не 0, то подобно предыдущему, надо было бы делить 1-й член этого остатка на 1-й член делителя; от этого получился бы 4-й член частного, и т. д. Можно было бы расположить делимое и делитель по возрастающим степеням одной и той же буквы и затем поступать так, как сейчас было сказано; при этом пришлось бы основываться на том, что низший член произведения равен произведению низшего члена множимого на низший член множителя. 71. Примеры.
Мы здесь не писали произведений 1-го члена делителя на 1-й, на 2-й и т. д. члены частного, потому что эти произведения всегда равны тем членам, под которыми они подписываются, и при вычитании всегда сокращаются. Обыкновенно так и делают. Кроме того, подписывая вычитаемые, мы писали их прямо с обратными знаками.
Подобным образом можем убедиться, что разности x5 — а5, х6 — а6... и вообще 72. Признаки невозможности деления многочленов. Из описанного процесса видно, что деление многочлена на многочлен нельзя выполнить в следующих случаях: а) Если показатель главной буквы в высшем члене делимого меньше показателя той же буквы в высшем члене делителя, потому что тогда нельзя получить высшего члена частного. б) Если показатель главной буквы в низшем члене делимого меньше показателя. той же буквы в низшем члене делителя, потому что тогда нельзя подучить низшего члена частного. в) Если показатели главной буквы в высшем и низшем членах делимого не меньше, соответственно, показателей этой буквы в высшем и низшем членах делителя, то еще нельзя сказать, чтобы деление было возможно. В этом случае, чтобы судить о возможности или невозможности деления, надо приступить к выполнению самого действия и продолжать его до тех пор, пока окончательно не убедимся в возможности или невозможности получить частное в виде многочлена. При этом надо различать 2 случая: I. Когда многочлены расположены по убывающим степеням главной буквы, то продолжают действие до тех пор, пока в остатке не получится 0 (тогда деление возможно и закончено), или пока не дойдут до такого остатка, 1-й член которого содержит главную букву с показателем меньшим, чем показатель 1-го члена делителя (тогда деление невозможно). Напр.:
Деление невозможно, потому что мы дошли до такого остатка, у которого 1-й член не делится на 1-й член делителя. II. Когда многочлены расположены по возрастающим степеням, то, сколько бы мы ни продолжали деление, никогда не получим такого остатка, у которого показатель 1-го члена быд бы меньше показателя 1-го члена делителя, потому что при таком расположении показатели главной буквы в первых членах остатков идут увеличиваясь. Напр.:
Продолжая действие дальше, мы получили бы в частном член — 4a3, но если бы возможно было получить целое частное (без остатка), то последний член его должен был бы быть 5a2 (от деления высшего члена делимого на высший член делителя); значит, деление невозможно. Замечание. О делении многочленов изложено более подробно во 2-й части, § 390 и след. Разложение на множители. 73. Предварительное замечание. Говоря об алгебраическом делении, мы указывали, что в некоторых случаях частное можно только обозначить знаком деления. Получаемые при этом выражения, вроде таких:
принято называть алгебраическими дробями по сходству этих выражений с арифметическими дробями. Мы вскоре увидим, что алгебраические дроби, подобно арифметическим, могут быть иногда упрощены посредством сокращения (т.е. посредством деления) делимого и делителя на их общие множители, если таковые окажутся. Для того, чтобы такое сокращение возможно было производить без затруднения, надо научиться разлагать алгебраические выражения на множители (подобно тому, как в арифметике для сокращения дробей надо уметь разлагать целые числа на составляющие их множители). 74. Разложение целых одночленов. Возьмем какой-нибудь целый одночлен, напр. 6a2b3. Так как он представляет собой произведение, то по одному его виду его сразу можно разложить на составляющие множители. Так: 6a2b3 =2•3 (аа) (bbb) = 2 • 3ааbbb. Соединяя эти сомножители в какие-нибудь группы (пользуясь сочетательным свойством умножения), мы можем для этого одночлена указать разнообразные разложения, напр.: 6a2b3=(6а)(аb3)=(2a2b)(3b2) = (Заb2)(2аb) и т. п. 75. Разложение многочленов. Укажем простейшие случаи, когда многочлен может быть разложен на множители. а) Так как (a + b — с) m = am + bm — cm, то и наоборот: am + bm — cm = (a + b — с) m. Таким образом, если все члены многочлена содержат общий множитель, то его можно вынести за скобки. Напр.: 1) x6—2x2 + 3x = x(x5 —2x + 3). 2) 16a2 — 4a3 = 4a2(4 — а). 3) 5m(x — 1) + 3n (х — 1) = (х — 1) (5m — 3n). б) Так как (а+ b)(а—b)=а2 — b2 то и наоборот: а2 — b2 = (а+ b)(а—b) Таким образом, двучлен, представляющий собой квадрат одного числа без квадрата другого числа, можно заменить произведением суммы этих чисел на их разность.
в) Так как (а + b)2 = a2 + 2аb + b2 и (а — b)2 = a2 — 2аb + b2, то и наоборот: a2 + 2аb + b2 = (а + b)2 = (а + b) (а + b) и a2 — 2аb + b2 = (а — b)2== (а — b) (а — b) , Значит, трехчлен, представляющий собой сумму квадратов каких-нибудь двух чисел, увеличенную или уменьшенную на удвоенное произведение этих чисел, можно заметешь квадратом суммы или разности этих чисел. Примеры. 1) a2 + 2а +1. Так как 1=12 и 2а = 2а • 1, то a2 + 2а +1 = (а + 1)2. 2) x4 + 4 — 4х2. Здесь x4 = (x2)2, 4 = 22 и 4х2 = 2x2•2; поэтому: x4 + 4 — 4х2 = (x2 — 2)2. Можно также написать, что x4 + 4 — 4х2 = (2— x2 )2, так как двучлены .x2 — 2 и 2— x2, будучи возвышены в квадрат, дают трехчлены, отличающиеся только порядком членов: (x2 — 2)2 = x4 + 4 — 4х2 ; (2— x2 )2 = 4 — 4х2 + x4. 3) —х + 25х2 + 0,01. Здесь есть два квадрата: 25х2 = (5x)2 и 0,01 = 0,12. Удвоенное произведение чисел 5х и 0,1 составляет: 2 •5х •0,1 = x. Так как в данном трехчлене оба квадрата стоят со знаком +, а удвоенное произведение (т. е. х) со знаком —, то —х + 25х2 + 0,01 = 25х2 — х + 0,01 = (5x — 0,1 )2 = (0,1 — 5x )2. 4) — х2 — у2 + 2xy. Вынесем знак — за скобки: — (х2+ у2— 2xy). Трехчлен, стоящий в скобках, очевидно, есть (х—у)2. Значит: — х2 — у2 + 2xy = — (х2+ у2— 2xy) = — (х — у)2 = — (у — х)2. г) Иногда многочлен можно разложить на множители посредством соединения его членов в некоторые группы.
Алгебраические дроби. 76. Отличие алгебраической дроби от арифметической. Как мы уже говорили раньше (§ 73), частное от деления двух алгебраических выражений в том случае, когда деление только указано, называется алгебраической дробью. Таковы, напр., выражения:
В таких выражениях делимое называется числителем, делитель — знаменателем, а то и другое — членами дроби. Вспомним, что и арифметическая дробь тоже представляет собою частное от деления числителя на знаменатель. Так, дробь 3/5 не только означает три таких доли, каких в единице содержится пять; дробь эта также означает пятую часть трех единиц, т. е. она есть частное от деления 3 на 5. Но отличие алгебраической дроби от арифметической состоит в том, что арифметическая дробь есть частное от деления одного целого положительного числа на другое целое положительное число, тогда как алгебраическая дробь есть частное от деления каких угодно чисел, как целых, так и дробных, как положительных, так и отрицательных. Напр., выражения:
нельзя назвать дробями арифметическими; это будут частные случаи дробей алгебраических. Таким образом, алгебраическая дробь представляет собою понятие более широкое, чем дробь арифметическая; она включает в себе дробь арифметическую как частный случай. Однако, несмотря на такое различие, все свойства арифметической дроби принадлежат, как это мы увидим в этой главе, и алгебраической дроби. 77. Основное свойство дроби. Так как дробь есть частное от деления числителя на знаменатель, а частное не изменяется от умножения (или деления) делимого и делителя на одно и то же число (кроме нуля) (Отдел1 § 34, е), то это же свойство принадлежит и дроби, т. е. величина дроби не изменяется, если её числитель и знаменатель умножим (или разделим) на одно и то же число (кроме нуля). Напр., если мы умножим числитель и знаменатель дроби
положим, на —4/9, то будем иметь: прежняя дробь новая дробь:
мы видим, что величина дроби осталась прежняя. Пользуясь этим свойством дроби, мы можем выполнять над алгебраическими дробями такие же преобразования, какие в арифметике указываются для дробей арифметических, т. е. мы можем сокращать, если возможно, дроби и приводить их, если нужно, к одному знаменателю. Рассмотрим эти преобразования и укажем еще некоторые, которые в арифметике не применяются. 78. Приведение членов дроби к целому виду. Если случится, что члены дроби сами содержат в себе дроби, то, умножая их на выбранное надлежащим образом число или на алгебраическое выражение, мы можем освободиться от этих дробей. Примеры.
79. Перемена знаков у членов дроби. Переменить знак на противоположный перед числителем и знаменателем дроби — это все равно, что умножить их на —1, от чего величина дроби не изменится. Так:
Заметим, что если переменим знак перед каким-нибудь одним членом дроби и в то же время переменим знак перед самою дробью, то величина дроби тоже не изменится; напр.:
Этими свойствами дроби можно иногда воспользоваться для некоторого ее преобразования; напр.:
80. Сокращение дробей. Чтобы сократить алгебраическую дробь, надо, если возможно, предварительно найти такое алгебраическое выражение, на которое оба члена дроби делятся, и затем их разделить на это выражение. Рассмотрим, как это всего удобнее делать в следующих двух случаях. а) Возьмем дробь, у которой оба члена — целые одночлены; напр.:
Коэффициенты 12 и 20 делятся на 4, а буквенные выражения делятся на а и на x2, Значит, эту дробь можно сократить на 4аx2:
(над дробью мы написали те общие множители, на которые дробь сокращаем; вместо деления 3ax на 5 мы разделили на 5 только коэффициент 3). б) Если у дроби числитель или знаменатель (или тот и другой)—многочлены, то надо предварительно разложить эти многочлены на множители (так, как было указано в § 75); если в числе их окажутся одинаковые, то на них дробь можно сократить. Примеры.
(вместо деления на 2 поставлено умножение на 1/2 что равносильно делению на 2). 81. Приведение дробей к общему знаменателю, а) Пусть требуется привести к общему знаменателю дроби со знаменателями, выраженными цифрами, напр, такие:
Для этого разложим знаменатели на простые множители: 3; 15 = 3•5; 18 = 2•3•3 и найдем их наименьшее кратное; это будет 2 • 3 • 3 • 5 = 90. Теперь найдем для каждого знаменателя дополнительный множитель, на который надо умножить этот знаменатель, чтобы получить вместо него 90. Эти дополнительные множители будут: 90:3 = 30; 90:15 = 6, 90:18 = 5. Чтобы дроби не изменили своей величины, надо и числители умножить на те же числа, на которые умножаем знаменатели:
(над дробями написаны дополнительные множители). б) Возьмем теперь дроби, у которых знаменатели — буквенные одночлены; напр.:
За общий знаменатель можно, очевидно, взять 30аb2. Дополнительными множителями тогда будут: 15аb, 10b и 6:
в) Далее возьмем дроби, у которых знаменатели многочлены; напр.:
Разложим каждый знаменатель на множители. Первые два не разлагаются, а третий = (a + b) (a — b). Значит, общим знаменателем будет a2 — b2, и мы получим:
г) Может, случиться, что никакая пара знаменателей не имеет общих множителей. Тогда надо поступить так, как это делается в подобном случае в арифметике, а именно: умножить числитель и знаменатель каждой дроби на произведение знаменателен всех остальных дробей. Напр.:
82. Сложение и вычитание дробей. По правилу деления многочлена на одночлен (§ 68) мы можем написать:
Читая эти равенства справа налево, находим: 1) чтобы сложить дроби с одинаковыми знаменателями, можно сложить их числители и под суммою подписать тот же знаменатель; 2) чтобы вычесть дроби с одинаковыми знаменателями, можно вычесть их числители и под разностью подписать тот же знаменатель; Если данные для сложения или вычитания дроби имеют разные знаменатели, то предварительно их следует привести к одному знаменателю. Напр.:
В результате вычитания получим:
83. Умножение дробей. Чтобы умножить дробь на дробь можно умножить числитель на числитель и знаменатель на знаменатель и первое произведение взять числителем, а второе знаменателем, т. е.
Напомним объяснение этого правила в применении к дробям арифметическим. Пусть дано умножить 2/3 • 4/5 Это значит: найти 4/5 от 2/3 (напр., найти 4/5 длины, равной 2/3 метра). Для этого надо сначала найти 1/5 от 2/3 а затем 4/5 от 2/3. Чтобы найти 1/5 от 2/3 надо 2/3 уменьшить в 5 раз; получим 2/15. Чтобы найти теперь 4/5 от 2/3, надо 2/15 увеличить в 4 раза; получим 8/15. Таким образом:
Теперь мы проверим это правило и для дробей алгебраических, когда числа а, b, с и d будут какие угодно. Предположим сначала, что все эти числа положительные, но не целые, а дробные. Пусть, напр.:
Подставим эти числа в равенство (1), вычислим отдельно его левую и его правую части и сравним результаты, которые получим (при вычислении будем руководствоваться правилами деления и умножения арифметических дробей):
(окончательного вычисления производить не будем). Теперь найдем правую часть равенства (1):
Сравнивай полученные результаты, мы видим, что они одинаковы, так как (согласно переместительному свойству умножения целых чисел) 2•8•5•4 = 2•5•8•4 и 3•7•6•9 = 3•6•7•9. Следовательно, равенство (1) остается верным и в этом случае. Теперь допустим, что какое-нибудь из чисел а, b, с и d сделалось oтрицательным. пусть напр., а = — 2/3 (b, с и d имеют прежние значения). Тогда дробь a/b сделается отрицательной, и вся левая часть равенства (1) также будет отрицательное число. В правой части произведение ас сделается отрицательным, и потому вся правая часть тоже будет отрицательное число. Абсолютная же величина у левой части и у правой останется прежняя. Значит, равенство (1) не нарушится. Так же убедимся, что равенство (1) останется верным и тогда, когда и другие числа сделаются отрицательными. Все то, что мы сейчас говорили о частном примере, может быть повторено о всяком другом примере; значит, равенство (1) верно при всяких значениях букв а, b, с и d. 84. Деление дробей. Чтобы разделить дробь на дробь, можно умножить числитель первой дроби на знаменатель второй, знаменатель первой на числитель второй и первое произведение взять числителем, а второе знаменателем, т. е.
Что это равенство верно для всяких чисел а, b, с, d, можно убедиться простою поверкою деления: умножив частное на делитель (по доказанному выше правилу умножения дробей), мы получим делимое:
85. Замечания. 1) Так как ad/bc = a/b • d/c , то правило деления можно высказать иначе: чтобы разделить дробь на дробь, можно первую дробь умножить на обратную второй. 2) Всякое целое алгебраическое выражение можно рассматривать как дробь, у которой числитель есть это целое выражение, а знаменателем служит 1; напр., a = a/1 ; 3x2 = 3x2 /1 и т. п. Поэтому данные нами правила действий над дробями можно применять и к таким случаям, когда какое-нибудь из данных выражений есть целое, стоит только это целое изобразить (хотя бы мысленно) дробью. Напр.:
86. Освобождение уравнения от знаменателей. Пусть дано уравнение:
Обратим 6 3/5 в неправильную дробь и приведем все члены к одному знаменателю:
Теперь умножим все члены на 10; тогда знаменатель 10 уничтожится, и мы получим уравнение без дробей:
Для избежания ошибки мы заключили двучлен 7x— 2 в скобки, чтобы показать, что знак —, стоявший в данном уравнении перед второю дробью, относится не к 7x, а ко всему двучлену 7x— 2 (к числителю второй дроби). Раскрыв эти скобки по правилу вычитания, получим:
Таким образом, чтобы освободить уравнение от знаменателей, надо привести все члены его к одному знаменателю и затем умножить их на этот знаменатель (другими словами, отбросить его). Отношение и пропорция. 87. Отношение. Часто приходится сравнивать между собою одну величину с другой величиной, однородной ей, с целью узнать, сколько раз первая величана содержит в себе вторую. Напр., мы с этою целью можем сравнивать вес какого-нибудь предмета с весом другого предмета, цену одного товара с ценою другого товара и т. п. Во всех таких случаях результат сравнения выражается числом, которое может быть и целым, и целым с дробью, и дробным. Пусть, напр., мы сравниваем длину а с другою длиною b, и результат сравнения оказался целым числом 3 .
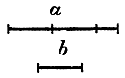
Это значит, что длина а содержит в себе длину b ровно 3 раза (другими словами, а больше b в 3 раза). Если результат сравнения есть целое число с дробью, напр. 21/2 , то это значит, что а содержит в себе b 21/2 раза (a больше b в 21/2 раза).
Если, наконец, результат сравнения есть дробь, положим 3/4 , то а не содержит в себе b ни одного раза, а составляет только 3/4 b.
Во всех этих случаях результат сравнения есть отвлеченное число, на которое надо умножить вторую величину, чтобы получить первую. Так, во взятых нами примерах: a = b • 3 ; a = b • 21/2 ; a = b • 3/4 ; Результат сравнения одной величины с другою однородною величиною принято называть отношением первой величины ко второй. Значит, отношением одной величины к другой однородной величине называется отвлеченное чиcло, на которое надо умножить вторую величину, чтобы получить первую. Так как это число есть частное от деления первой величины на вторую, то отношение обозначается знаком деления. Так, можно писать: a/b (или a : b) =3; a/b = 21/2 a/b = 3/4. и т. п. Величины, между которыми берется отношение, называются членами отношения, причем первая величина называется предыдущим членом, а вторая — последующим. Если величины измерены одною и тою же единицей и выражены числами, то отношение их можно заменить отношением этих чисел. Напр., отношение двух весов, одного в 80 г, а другого в 15 г, равно отношению чисел 80 и 15, т. е. оно равно частному 80:15, что составляет 51/3; равным образом отношение угла в 30° к прямому углу равно частному 30:90, т. е. дроби 1/3 Сравнивать между собою приходится большею частью величины положительные; поэтому оба члена отношения и само отношение мы будем предполагать выраженными числами положительными. 88. Зависимость между отношением и его членами та же самая, какая существует между делимым, делителем и частным. Так: а) Предыдущий член равен последующему, умноженному на отношение (делимое равно делителю, умноженному на частное). Если, напр., отношение некоторого неизвестного числа х к числу 100 равно 21/2 , то х = 100 • 21/2 = 250. б) Последующий член равен предыдущему, деленному на отношение (делитель равен делимому, деленному на частное). Так, если известно, что 15 : х = 5, то х = 15 : 5 = 3. в) Отношение не изменится, если оба его члена умножим или разделим на одно и то же число (частное не изменится, если...). 89. Приведение членов отношения к целому виду. Умножая оба члена отношения на одно и то же число, мы можем отношение с дробными членами заменить отношением целых чисел. Так, отношение 7/3 : 5 по умножении его членов на 3 обратится в отношение целых чисел 7:15; отношение 9/14 : 10/21 после умножения его членов на общий знаменатель 42 обратится также в отношение целых чисел 27 : 20. 90. Сокращение отношения. Если оба члена отношения — целые числа, делящиеся на какой-нибудь общий делитель, то такое отношение можно сократить. Так, отношение 42 : 12 по разделении.его членов на 6 будет 7:2. 91. Обратные отношения. Если мы переставим члены отношения, т. е. предыдущий член сделаем последующим, и наоборот, то получим новое отношение, которое называется обратным прежнему. Так, отношение метра к сантиметру обратно отношению сантиметра к метру; первое равно числу 100, второе равно обратному числу 0,01. 92. Пропорция. Заметив, что отношение килограмма к грамму равно 1000 и что отношение километра к метру также равно 1000, мы можем написать равенство:
или килограмм : грамм = километр: метр, что читается так: отношение килограмма к грамму равно отношению километра к метру; или так: килограмм относится к грамму так, как километр относится к метру (или еще так: килограмм больше грамма во столько раз, во сколько раз километр больше метра). Равенство двух отношений принято называть пропорцией. Конечно, величины, входящие в каждое отношение, должны быть однородны; так, в нашем примере величины первого отношения — веса, а величины второго отношения — длины. Из четырех величин, составляющих пропорцию, первая и четвертая называются крайними членами, вторая и третья — средними членами, первая и третья — предыдущими, вторая и четвертая — последующими. Последняя величина называется также четвертой пропорциональной к первым трем величинам. Мы будем предполагать, что все четыре члена пропорции выражены числами; такую пропорцию мы будем называть числовою. 93. Основное свойство числовой пропорции. Пусть мы имеем такие числовые пропорции: 21/7 = 15/5 (каждое отношение = 3) и
Возьмем в каждой пропорции произведение крайних членов и произведение средних и сравним их между собою. В первой пропорции произведение крайних равно 21•5=105, и произведение средних равно 7•15=105; во второй пропорции произведение крайних = 2 1/2 • 3 = 7 1/2 и произведение средних = 3/4•10 = 7 1/2 Таким образом, в каждой из взятых пропорций произведение крайних членов равно произведению средних. Чтобы показать, что свойство это принадлежит всякой числовой пропорции, возьмем пропорцию в буквенном виде: a/b = с/d Так как каждое из двух отношений, составляющих пропорцию, есть частное от деления предыдущего члена на последующий, то можно сказать, что пропорция есть равенство двух дробей. Приведем эти дроби к общему знаменателю bd.
Умножим теперь обе части равенства на bd (от чего равенство не нарушится); тогда общий знаменатель сократится, и мы получлм равенство: ad = cb, выражающее, что во всякой числовой пропорции произведение крайних членов равно произведению средних. Отсюда выходит, что каждый крайний член пропорции равен произведению средних, деленному на другой крайний, и каждый средний член пропорции равен произведению крайних, деленному на другой средний. Это дает нам возможность быстро решать уравнения, данные в виде пропорций; напр., из уравнения 10/x = 45/20 выводим прямо: х = 10•20/45 = 44/9. 94. Обратное предложение. Положим, мы имеем 4 таких числа, что произведение двух из них равно произведению двух остальных, напр.: 5•12 = 30•2. Такое равенство мы можем превратить в ряд пропорций. Для этого разделим обе части на каждое из таких произведений: 5•30; 5•2; 12•30; 12•2, в которых один сомножитель взят из одного данного произведения, а другой — из другого. Тогда получим 4 других равенства (если равные числа разделим на равные, то получим равные), а именно:
Сократив все эти дроби, найдем:
Мы получим таким образом 4 пропорции, в которых крайними членами служат сомножители одного из данных произведений, а средними членами — сомножители другого данного произведения. Подобно этому равенство 0,3 • 4 = 6 • 0,2 мы можем превратить в такие пропорции:
или равенство: 5x = 3y можем превратить в пропорции: 5:3 = y : x; x : y = 3 : 5, и т. п. Таким образом, если произведение двух чисел равно произведению двух других чисел, то из этих 4 чисел можно составить пропорции, беря сомножители одного произведения за крайние члены, а сомножители другого произведения за средние члены пропорций. 95. Следствие. Во всякой числовой пропорции можно переставить средние члены между собою, крайние члены между собою, или средние поставить на место крайних, и наоборот, так как от таких перестановок не нарушится равенство между произведением крайних и произведением средних и, следовательно, не нарушится пропорциональность чисел. 96. Среднее геометрическое. Возьмем пропорцию, в которой средние члены одинаковы; например: 33:12 = 12:4. Повторяющийся член такой пропорции называется средним геометрическим числом двух остальных членов пропорции: 12 есть среднее геометрическое 36 и 4. Таким образом, если требуется найти среднее геометрическое двух чисел а и b, то, обозначив его буквой х, мы можем написать пропорцию: a : x = x : b откуда x2 = ab Значит, среднее геометрическое двух данных чисел есть такое третье число, квадрат которого равен произведению данных чисел. Напр., среднее геометрическое 25 и 4 равно 10, потому что 102 = 25 • 4 3). 97. Среднее арифметическое. Средним арифметическим нескольких данных чисел называется частное от деления суммы этих чисел на число их. Напр., среднее арифметическое 4 чисел: 10, —2, —8 и 12 равно:
Среднее арифметическое обладает тем свойством, что если при сложении данных чисел мы заменим каждое из них средним арифметическим, то от этой замены сумма не изменится. Так, сумма чисел 10, — 2, —8 и 12 равна 12 и сумма 3+3+3+3 также равна 12. Положим, напр., что производительность фабрики в течение первых четырех месяцев текущего года, сравнительно с производительностью ее в декабре предыдущего года, повысилась: в январе на 10°/о, в феврале на —2%, в марте на — 8% (значит, в последние 2 месяца производительность понизилась) и в апреле на +12%. Тогда можно сказать, что среднее повышение производительности за эти 4 месяца составляет 3% в месяц. Это надо понимать так, что производительность фабрики за все 4 месяца оказалась такая же, какая была бы, если бы она повышалась в каждый месяц одинаково, именно на 3% (сравнительно с декабрьской производительностью). В подобном же смысле говорят часто о среднем доходе, о средней скорости движения, о средней плотности населения и т. п. Во всех таких выражениях подразумевается, что речь идет о среднем арифметическом. 98. Производные пропорции. Из всякой пропорции, помимо перестановки ее членов, можно получить еще некоторые другие пропорции, называемые производными. Укажем две из них. Если каждое из равных отношений, составляющих пропорцию, увеличим или уменьшим на 1, то равенство между отношениями, очевидно, не нарушится. Поэтому, если
Приведя 1 к общему знаменателю с тою дробью, к которой она приложена или от которой вычтена, мы получим:
Выведенные нами две производные пропорции мы можем высказать так: во всякой пропорции сумма или разность членов первого отношения относится к последующему члену этого отношения так, как сумма или разность членов второго отношения относится к последующему члену этого отношения. Разделим равенство (1) и (2) на данное равенство а/b = c/d тогда знаменатели b и d сократятся, и мы получим еще две производные пропорции:
которые можно высказать так: сумма или разность членов первого отношения относится к предыдущему члену этого отношения так, как сумма или разность членов второго отношения относится к предыдущему члену этого отношения. Разделив почленно равенство (1) на равенство (2), найдем еще следующую производную пропорцию:
которую можно высказать так: сумма членов первого отношения относится к их разности так, как сумма членов второго отношения относится к их разности. Переставив средние члены в двух производных пропорциях, получим еще другие производные пропорции, которые полезно заметить:
99. Свойство равных отношений. Возьмем несколько равных отношений, напр., таких: 30/10 = 6/2 = 15/5 (каждое отношение =3). Сложим все предыдущие члены между собою и все последующие члены между собою и посмотрим, в каком отношении находятся эти две суммы. Сумма предыдущих равна: 30 + 6 + 15 = 51; сумма последующих: 10 + 2 + 5 = 17. Мы видим, что отношение первой суммы ко второй равно тому же числу 3, какому равны данные отношения, так что можно написать:
Чтобы показать, что это свойство общее, возьмем несколько равных отношений в буквенном виде:
Так как предыдущий член равен последующему члену, умноженному на отношение, то a = bq, c = dq, e = fq , . . . и следовательно, а + с + е + . . . = bq + dq + fq + . . . т. е. а + с + е . . . =q( b + d + f + . . .) Разделим обе части этого равенства на сумму b + d + f + . . .
следовательно:
Таким образом, если несколько отношений равны между собою, то сумма всех предыдущих членов их относится к сумме всех последующих, как какой-нибудь из предыдущих относится к своему последующему. Так как всякая пропорция состоит из двух равных отношений, то указанное свойство принадлежит также и пропорции. 100. Арифметическое применение. (Пропорциональное деление.) Пусть требуется число 60 разделить на три части пропорционально числам б, 7 и 8. Это надо понимать так, что требуется разделить 60 на такие три части х, у и z, чтобы х так относился к 5, как у относится к 7 и как z относится к 8, т. е. чтобы x/5 = y/7 = z/8 Применяя свойства равных отношений, найдем:
Но x + y + z = 60 значит:
Отсюда находим:
101. Геометрическое применение. Пусть два многоугольника подобны и стороны одного будут а, b, с, d,..., а сходственные, стороны другого а', b', с', d',... Тогда a/a' = b/b' = c/c' = d/d' = ...
т. е. периметры подобных многоугольников относятся, как сходственные стороны. Замечание. Производными пропорциями и свойством равных отношений можно иногда пользоваться для скорейшего решения уравнения, данного в виде пропорции. Приведем примеры.
Составим производную пропорцию: сумма членов первого отношения относится к последующему члену того же отношения так, как . . . Тогда получим: 3/x = 47/7 откуда x = 21/47
Составим производную пропорцию: сумма членов первого отношения относится к их разности так, как . . . Тогда получим:
Составим новую пропорцию: сумма предыдущих относится к сумме последующих так, как . . . :
Теперь составим производную пропорцию: сумма членов первого отношения относится к последующему члену этого отношения так, как . . . :
Пропорциональная зависимость (прямая и обратная). 102. Пропорциональная зависимость. Каждый из опыта знает, что если объем воды увеличится (или уменьшится) в каком-нибудь отношении, то и вес ее увеличится (или уменьшится) в том же отношении. Напр., 1 л воды весит 1 кг, 2 л воды весят 2 кг, 21/2 л воды весят 21/2 кг и т. д. (предполагается, конечно, что все прочие условия, влияющие на вес воды, остаются неизменными; напр., вода берется одинаково чистая, при одной и той же температуре и пр.). Такая зависимость между объемом воды и ее весом называется пропорциональною зависимостью. Вообще, если говорят, что две величины находятся между собою в пропорциональной зависимости (или пропорциональны друг другу), то это значит, что с увеличением (или уменьшением) одной из них в каком-нибудь отношении другая тоже увеличивается (или уменьшается) в таком же отношении. Так, стоимость товара, продаваемого на вес, пропорциональна его весу; плата рабочим пропорциональна числу их (при одинаковых прочих условиях); величина дроби пропорциональна ее числителю (при неизменном знаменателе); площадь прямоугольника пропорциональна его основанию при неизменной высоте и пропорциональна его высоте при неизменном основании и т. п. 103. Выражение пропорциональной зависимости формулой. Положим, мы решаем такую задачу: Поезд железной дороги, двигаясь равномерно, проходит каждый час 30 км. Какое пространство пройдет этот поезд в а часов (а может быть числом целым и дробным)? Пусть в а часов поезд пройдет х км. Расположим данные и вопрос задачи так: в 1 час проходится 30 км; в а час „ х км. При равномерном движении пространство, проходимое в течение какого-нибудь времени, пропорционально этому времени. Поэтому x должно быть более или менее 30 и во столько раз, во сколько а больше или меньше 1. Значит, мы можем записать пропорцию: х : 30 = а : 1, откуда x = 30а. Мы получили, таким образом, формулу, по которой можно вычислить пространство, пройденное в любое число а часов. Напр., в 2 часа будет пройдено 30 км • 2, в 31/2 часа 30 км • 31/2. в 3/4 часа 30 км • 3/4 . Значит, в выведенной формуле числа х и а будут переменные (соответствующие друг другу), число же 30 постоянное (означающее пространство, проходимое поездом в 1 час, т. е. скорость движения). Из задач, подобных приведенной сейчас, мы усматриваем, что если две величины пропорциональны, то численное значение одной из них равно некоторому постоянному числу, умноженному на соответствующее численное значение другой величины. Обратно, если зависимость между двумя какими-нибудь переменными величинами, которые мы обозначим у и х, выражается формулой вида у = kх, где k есть некоторое постоянное для этих величин число, то такие величины пропорциональны, так как из этой формулы видно, что с увеличением (или уменьшением) величины х в каком-нибудь отношении другая величина у тоже увеличивается (или уменьшается) и притом в том же самом отношении. Напр., как известно из геометрии, длина С окружности радиуса R выражается формулой: C = 6,28R (С = 2πR), в которой R и C - переменные величины, а 6,28 — постоянное число; тогда мы можем заключить, что длина окружности пропорциональна ее радиусу. Постоянное число, входящее сомножителем в подобные формулы, называется коэффициентом пропорциональности тех переменных величин, к которым формула относится. 104. Обратная пропорциональная зависимость. Иногда случается, что две переменные величины зависят одна от другой так, что с увеличением одной из них другая уменьшается и притом уменьшается в таком же отношении, в каком первая увеличивается. Такие величины называются обратно пропорциональными (а величины просто пропорциональные называются иногда прямо пропорциональными). Напр., число часов, в течение которого поезд железной дороги проходит весь путь от Москвы до Ленинграда, обратно пропорционально средней скорости движения этого поезда, так как с увеличением скороcти в 11/2 pаза, в 2 раза..., вообще в некотором отношении, число часов, в течение которого поезд пройдет расстояние от Москвы до Ленинграда, уменьшится в 11/2 pаза, в 2 раза..., вообще в том же отношении, в каком скорость увеличилась. Подобно этому вес товара, который можно купить на данную сумму денег, напр, на 100 руб., обратно пропорционален цене килограмма этого товара; время, в течение которого выполняется рабочими заданная им работа, обратно пропорционально числу этих рабочих (конечно, при уcловии, что все рабочие работают одинаково успешно); величина дроби обратно пропорциональна ее знаменателю (при постоянном числителе), и т. п. Замечание. Для того, чтобы две зависящие друг от друга величины были пропорциональны (прямо или обратно), не достаточно только того признака, что с увеличением одной величины другая тоже увеличивается (для прямой пропорциональности), или что с увеличением одной величины другая уменьшается (для обратной пропорциональности). Напр., если какое-нибудь слагаемое увеличится, то и сумма увеличится; но было бы ошибочно сказать, что сумма пропорциональна слагаемому, так как если увеличим слагаемое, положим в 3 раза, то сумма хотя и увеличится, но не в 3 раза. Подобно этому, нельзя, напр., сказать, что разность обратно пропорциональна вычитаемому, так как если увеличится вычитаемое, положим в 2 раза, то разность хотя и уменьшится, но не в 2 раза. Нужно, чтобы увеличение или уменьшение обеих величин происходило в одинаковое число раз (в одинаковом отношении). 105. Выражение обратной пропорциональной зависимости формулой. Положим, мы решаем задачу: один рабочий может выполнить некоторую работу в 12 дней; во сколько дней сделают ту же работу а рабочих? Обозначим искомое число буквой х и расположим для ясности данные и вопрос задачи так: 1 рабочий исполняет работу в 12 дней а рабочих исполняют „ „ х дней. Очевидно, что число дней, потребное для выполнения одной и той же работы, обратно пропорционально числу рабочих. Поэтому (x должно быть меньше 12 и во столько раз, во сколько а б о л ь ш е 1 (другими словами, во сколько 1 меньше а). Значит, отношение x :12 должно равняться не отношению а :1 , как это было бы при прямой пропорциональной зависимости, а обратному отношению 1 : а. Значит, мы можем написать пропорцию: x :12 = 1 : а откуда х = 12/a . По этой формуле мы можем находить число дней х, потребное для исполнения данной работы, при всяком числе а рабочих; напр., 2 рабочих окончат работу в 12/2 дней, 3 рабочих в 12/3 дней и т. п. Значит, числа х и а в этой формуле переменные, а число 12 постоянное, означающее, во сколько дней исполняется работа одним рабочим. Из задач, подобных решенной сейчас, мы можем усмотреть, что если две какие-нибудь величины (кoторые мы обозначим буквами х и у) обратно пропорциональны, то численное значение одной из них равно некоторому постоянному числy (обозначим его k), деленному на соответствующее значение другой величины, т. е. у = k/x, если у и х представляют собою соответствующие значения этих величин. Так как формулу у = k/x можно представить так: ху = k, то зависимость между обратно пропорциональными величинами можно высказать еще иначе: если две величины обратно пропорциональны, то произведение двух соответствующих друг другу, численных значений этих величин равно постоянному числу. Обратно, если зависимость между двумя переменными величинами выражается формулой: у = k/x или ху = k. где k есть постоянное число, то эти величины обратно пропорциональны, так как из формулы видно, что если величина х увеличивается в несколько раз, то величина у уменьшается во столько же раз. Напр., из физики известно, что при неизменной температуре произведение объема V данной массы газа на его упругость h есть величина постоянная; это, другими словами, означает, что упругость данной массы газа обратно пропорциональна его объему (при одной и той же температуре). Замечание. Равенство у = k/x может быть написано иначе, так: у = k • 1/x В этом виде оно выражает, что величина у прямо пропорциональна величине дроби 1/x. Значит, если число у обратно пропорционально числу х, то можно также сказать, что число у прямо пропорционально обратной величине числа x, т. е. 1/x. _________________
|
,
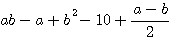
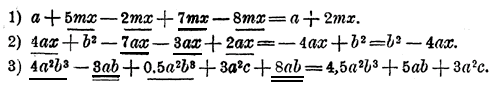
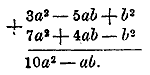
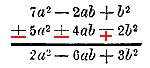
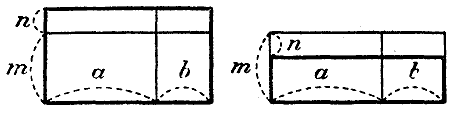
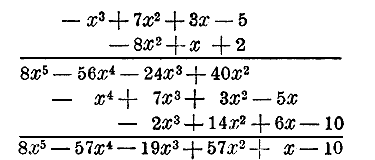
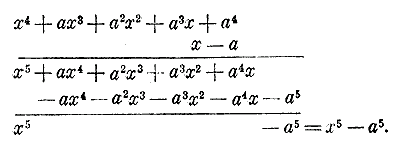
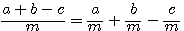
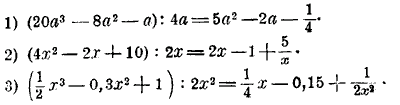
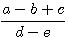, или (а — b + с ): (d — e).
и т. п.,
