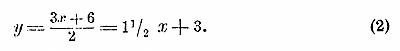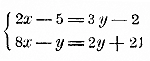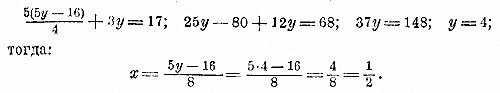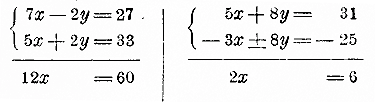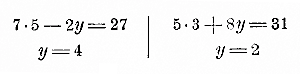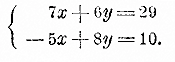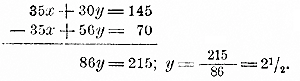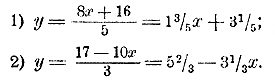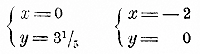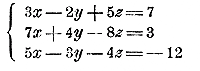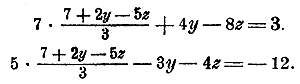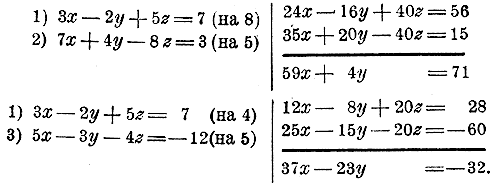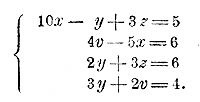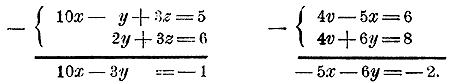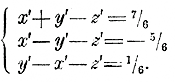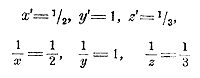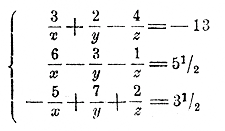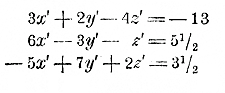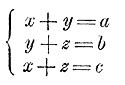| АЛГЕБРА В НАЧАЛО | ||
|
ОТДЕЛ ПЯТЫЙ. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ. Глава первая. Система двух уравнений с двумя неизвестными. Система двух уравнений с двумя неизвестными. 137. Задача. Из опыта найдено, что слиток из серебра и меди весом в 148 кг теряет в воде весу 142/3 кг. Определить, сколько в нем серебра и сколько меди, если известно, что в воде 21 кг серебра теряют 2 кг, а 9 кг меди теряют 1 кг. Положим, что в данном слитке содержится серебра х кг, а меди у кг. Тогда одно уравнение будет: х + у =148. Для составления другого уравнения примем во внимание, что если 21 кг серебра теряют в воде 2 кг весу, то это значит, что 1 кг серебра теряет в воде 2/21 кг. Тогда х кг должны терять в воде 2/21 х кг весу. Подобно этому, если 9 кг меди теряют в воде 1 кг, то это значит, что 1 кг меди теряет 1/9 кг; следовательно, у кг меди теряют 1/9 у кг. Поэтому второе уравнение будет: 2/21 х + 1/9 у = 142/3 Мы получили таким образом два уравнения с 2 неизвестными: х + у =148 и 2/21 х + 1/9 у = 142/3 = 44/3 Второе уравнение можно упростить, освободив его от дробей. Для этого приведем все дроби к одному знаменателю: 6/63 х + 7/63 у = 924/63 Теперь умножим обе части уравнения на 63; получим равносильное уравнение: х + у = 924 Мы имеем теперь два уравнения: х + у =148 и 6х + 7у = 924 Мы можем решить эти два уравнения несколькими способами. Напр, так: из первого уравнения определим х в зависимости от у (другими словами, определим х как функцию от у): x = 148 — у. Так как во втором уравнении буквы х и у означают те же числа, что и в первом уравнении, то мы можем во второе уравнение подставить вместо х разность 148 — у. 6 ( 148 — у ) + 7у = 924 Решим это уравнение с одним неизвестным: 888 — 6у + 7у = 924; у = 924 — 888 = 36. Тогда х = 148 — 36 = 112. Таким образом, в данном слитке содержится 112 кг серебра и 36 кг меди. 138. Нормальный вид уравнения первой степени с двумя неизвестными. Возьмем такой пример уравнения с 2 неизвестными: 2 (2х + 3y — 5) = 5/8 (х + 3) + 3/4 ( y — 4). С целью упростить это уравнение, сделаем в нем тот же ряд преобразований, какой был указан раньше для уравнения с 1 неизвестным, а именно. 1) Раскроем скобки: 4х + 6y — 10 = 5/8 х + 15/8 + 3/4 y — 3 2) Освободимся от знаменателей, умножив все члены на 8: 32х + 48y — 80 = 5х + 15 + 6 y — 24 3) Перенесем неизвестные члены в одну часть уравнения, а известные в другую: 32х + 48y —5х — 6 y = 15 — 24 + 80 4) Сделаем приведение подобных членов: 27x + 42y = 71. Таким образом, данное уравнение после указанных преобразований оказывается такого вида, при котором в левой части уравнения находятся только два члена: один с неизвестным х (в первой степени) и другой с неизвестным у (в первой степени), правая же часть уравнения состоит только из одного члена, не содержащего неизвестных. Коэффициенты при х и у могут быть или оба положительные (как во взятом нами примере), или оба отрицательные (этот случай, впрочем, можно свести на предыдущий, умножив все члены уравнения на — 1), или один положительный, а другой отрицательный; член, стоящий в правой части, может быть или положительным числом (как в настоящем примере), или отрицательным и даже нулем. Обозначив коэффициенты при х и у буквами а и b и член, не содержащий неизвестных, буквою с, мы можем уравнение с 2 не известными 1-й степени в общем виде представить так: ах + bу = с. Такой вид уравнения называется нормальным видом уравнения 1-й степени с 2 неизвестными. 139. Неопределенность одного уравнения с 2 неизвестными. Одно уравнение c 2 неизвестными имеет бесчисленное множество корней. Действительно, если для одного какого-нибудь неизвестного мы назначим произвольное число и это число подставим в уравнение, то тогда мы получим уравнение только с одним другим неизвестным; из этого уравнения можно найти это другое неизвестное. Так, если в уравнении 3x— 2y = — 6 мы примем, что у = 2, то уравнение будет 3x — 4 = —6, откуда найдем: 3x = — 2 и x = — 2/3. Значит, если у = 2, то x = — 2/3. Теперь назначим для у какое-нибудь другое число, напр., у = 1. Тогда получим 3х— 2 = — 6, 3х = — 4, х = —11/3. Значит, если у = 1, то .х = —11/3 . Таким образом, мы можем найти сколько угодно пар решений, и, следовательно, уравнение окажется неопределенным. Это же можно показать и графически. Из уравнения: 3x— 2y = — 6 (1) определим у как функцию от х :
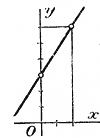
Надо привыкнуть быстро и безошибочно из данного уравнения определять одно неизвестное как функцию другого неизвестного. Так, чтобы из нашего уравнения определить у как функцию от х, надо мысленно перенести член —2y направо, а член —6 налево, затем части уравнения переставить и разделить их на 2; писать надо прямо результат этих преобразований. Функция эта есть двучлен 1-й степени, а такой двучлен изображается в координатных осях в виде прямой линии, которую мы можем построить по двум точкам (отдел3 § 118), напр. таким:
Координаты каждой точки этой прямой удовлетворяют уравнению (2) и, следовательно, удовлетворяют и уравнению (1); а так как на прямой бесчисленное множество точек, то уравнение (1) имеет бесчисленное множество решений. 140. Система уравнений. Принято говорить, что несколько уравнений образуют систему, если во всех этих уравнениях каждая из букв х, у, . . означает одно и то же число для всехуравнений. Если, напр., два уравнения:
рассматриваются при том условии, что буква х означает одно и то же число в обоих уравнениях, равным образом и буква у, то такие уравнения образуют систему. Это бывает всякий раз в том случае, когда уравнения составлены из условий одной и той же задачи. Укажем три способа решения системы 2 уравнений 1-й степени с 2 неизвестными. 141. Способ подстановки. Этот способ мы уже применяли1 раньше, когда решали задачу о слитке из серебра и меди (§ 137). Возьмем теперь более сложный пример: 8x — 5y = — 16; 10x + 3у =17 (оба уравнения мы привели к нормальному виду). Из одного уравнения, напр, из первого, определим одно какое-нибудь неизвестное, напр, х, как функцию другого неизвестного:
Так как второе уравнение должно удовлетворяться теми же значениями, как и первое, то мы можем подставить в него вместо х найденное выражение, от чего получим уравнение с одним неизвестным у:
Решим это уравнение:
Мы могли бы определить из одного уравнения у как функцию от х и полученное выражение подставить на место у в другое уравнение; тогда мы получили бы уравнение с неизвестным х. Способ этот особенно удобен тогда, когда коэффициент при каком-нибудь неизвестном равен 1; тогда всего лучше определить это неизвестное как функцию другого неизвестного (не придется делить на коэффициент), и т. д. Напр.:
Из второго уравнения находим: у = 22— 4х. Тогда первое уравнение дает: 3х — 2 (22 — 4x)=11; 3x —44 + 8x = 11; 11x = 44+ 11 = 55. x = 55/11 =5; y = 22 — 4•5 = 2. Правило. Чтобы решить систему двух уравнений с 2 неизвестными способом подстановки, надо определить из какого-нибудь уравнения одно неизвестное как функцию другого неизвестного и полученное выражение подставить в другое уравнение; от этого получается уравнение с одним неизвестным. Решив его, находят это неизвестное. Подставив найденное число в выражение, выведенное раньше для первого неизвестного, находят и это другое неизвестное. 142. Способ сложения или вычитания. Предположим сначала, что в данной системе уравнений (приведенных предварительно к нормальному виду) коэффициенты при каком-нибудь неизвестном, напр, при у, будут одинаковы. При этом могут представиться два случая: 1) знаки перед такими коэффициентами разные и 2) знаки одинаковые. Рассмотрим эти два случая параллельно. Пусть, напр., даны две системы:
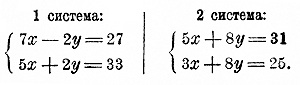
Если сложим почленно уравнения первой системы и вычтем почленно уравнения второй системы, то неизвестное у исключится:
Откуда: х = 5 х =3 Подставив в одно из данных уравнений вместо х найденное для него число, найдем у:
Возьмем теперь систему, в которой коэффициенты различны, напр. такую:
Мы можем тогда предварительно уравнять коэффициенты при каком-нибудь одном неизвестном, напр, при х. Для этого найдем кратное (лучше всего наименьшее) коэффициентов 7 и 5 (это будет 35) и умножим обе части каждого уравнения на соответствующий дополнительный множитель (как это делается при приведении дробей к общему знаменателю):
После этого остается только сложить или вычесть преобразованные уравнения. В нашем примере знаки перед коэффициентами х разные; поэтому уравнения надо сложить:
Теперь первое уравнение дает: 7x + 6• 21/2 = 29; 7x + 15 = 29; 7x = 14; х = 2. Правило. Чтобы решить систему двух уравнений с 2 неизвестными способом сложения или вычитания , надо сначала уравнять в обоих уравнениях коэффициенты при каком-нибудь одном неизвестном, а потом сложить оба уравнения, если знаки перед этими коэффициентами разные, или вычесть уравнения, если знаки одинаковые. 143. Графическое решение. Пусть дана система: 8х — 5у = — 16; 10x + 3у = 17. Из каждого уравнения определим у как функцию от х :
Графики этих функций должны быть прямые линии. Построим на одном чертеже каждую из них по двум точкам, напр, по таким: из уравнения.......у = 13/5 x + 31/5 :
из уравнения.......у = 52/3 — 31/3 х:
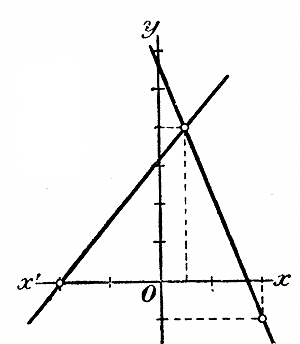
На чертеже видно, что две прямые пересекаются в точке, абсцисса которой равна 1/2, а ордината 4. Эти значения х и у, удовлетворяя обоим уравнениям, и будут решениями данной системы. Замечания. 1) Если бы случилоcь, что прямые,выражающие данные уравнения, оказались параллельными и, следовательно, не существовало бы точки их пересечения, то это значило бы, что уравнения не имеют корней. 2) Может иногда случиться, что 2 прямые сливаются в одну; тогда координаты всякой точки этой прямой удовлетворяют данным уравнениям, и, значит, система неопределенна. 3) В конце 2-й части этой книги указаны общие формулы для решения системы двух уравнений с 2 неизвестными первой степени (§ 396 и след.). Система трех уравнений с тремя неизвестными. 144. Нормальный вид уравнения первой степени с тремя неизвестными. Если в уравнении 1-й степени с 3 неизвестными х, у и z сделаны те же преобразования, какие были нами раньше указаны для уравнения с 1 и 2 неизвестными, то мы приведем уравнение к такому виду (называемому нормальным), при котором в левой части уравнения находятся только три члена: один с х, другой с у и третий с z, а в правой части будет один член, не содержащий неизвестных. Таково, напр., уравнение: 5х — 3у — 4z = —12. Общий вид его есть следующий: ах + by + cz = d, где а, b, с и d какие-нибудь относительные числа. 145. Неопределенность двух и одного уравнения с тремя неизвестными. Положим, нам дана система 2 уравнений с 3 неизвестными: 5х— 3у + z = 2; 2х + у— z = 6. Назначим одному неизвестному, напр. z, какое-нибудь произвольное число, положим 1, и подставим это число на место z : Мы получили таким образом систему 2 уравнений с 2 неизвестными. Решив ее каким-нибудь способом, найдем: х = 2, у = 3; значит, данная система с 3 неизвестными удовлетворяется при х = 2, у = 3 и z =1. Дадим теперь неизвестному z какое-нибудь иное значение, напр. z = 0, и подставим это значение в данные уравнения: 5х— 3у = 2; 2х + у = 6. Мы снова получим систему 2 уравнений с 2 неизвестными. Решив ее каким-нибудь способом, найдем: x = 20/11= 1 9/11 y = 2 4/11 Значит, данная система удовлетворяется при x = 1 9/11 y = 2 4/11 и z = 0. Назначив для z еще какое-нибудь (третье) значение, мы снова получим систему 2 уравнений с 2 неизвестными, из которой найдем новые значения для х и у. Так как для z мы можем назначать сколько угодно различных чисел, то и для х и у можем получить сколько угодно значений (соответствующих взятым значениям z). Значит, 2 уравнения с 3 неизвестными допускают бесчисленное множество решений; другими словами, такая система неопределенна. Еще большая неопределенность будет, если имеется всего 1 уравнение c 3 неизвестными. Тогда можно будет для каких-нибудь 2 неизвестных назначить произвольные числа; третье же неизвестное найдется из данного уравнения, если подставить в него значения, взятые произвольно для двух неизвестных. 146. Система 3 уравнений с 3 неизвестными. Для того, чтобы можно было найти определенные численные значения для трех неизвестных х, у и z, необходимо, чтобы была задана система 3 уравнений. Такая система может быть решена способом подстановки, а также и способом сложения или вычитания уравнений. Покажем применение этих способов на следующем примере (каждое уравнение предварительно приведено к нормальному виду):
147. Способ подстановки. Из какого-нибудь уравнения, напр, из первого, определим одно неизвестное, напр, х, как функцию от двух остальных неизвестных:
Так как во всех уравнениях х означает одно и то же число, то мы можем подставить найденное выражение на место х в остальные уравнения:
Мы приходим таким образом к системе 2 уравнений с 2 неизвестными у и z. Решив эту систему по какому-нибудь из способов, указанных раньше, найдем численные значения для у и г. В нашем примере это будут значения: у = 3, z = 2; подставив эти числа в выражение, выведенное нами для х, найдем и это неизвестное:
Таким образом, предложенная система имеет решение х = 1, у = 3, z = 2 (в чем можно убедиться поверкою). 148. Способ сложения или вычитания. Из 3 данных уравнений возьмем какие-нибудь два, напр. 1-е и 2-е, и, уравняв в них коэффициенты перед одним неизвестным, напр, перед z, исключим из них это неизвестное способом сложения или вычитания; от этого получим одно уравнение c 2 неизвестными х и у. Потом, возьмем какие-нибудь два других уравнения из 3 данных, напр. 1-е и 3-е (или 2-е и 3-е), и тем же способом исключим из них то же неизвестное т. е. z ; от этого получим еще одно уравнение с х и у:
Решим получившиеся два уравнения: x = 1, у = 3. Вставим эти числа в одно из трех данных уравнений, напр, в первое: 3 • 1 — 2 • 3 + 5z = 7; 5z = 7 —3 + 6 = 10; z =2. Замечание. Теми же двумя способами мы можем привести систему 4 уравнений с 4 неизвестными к системе 3 уравнений с 3 неизвестными (а эту систему —к системе 2 уравнений с 2 неизвестными и т. д.). Вообще систему m уравнений с m неизвестными мы можем привести к системе m — 1 уравнений с m — 1 неизвестными (а эту систему к системе m — 2 уравнений с m — 2 неизвестными и т. д.). Некоторые особые случаи систем уравнений. 149. Случай, когда не все неизвестные входят в каждое из данных уравнений; напр.:
В этом случае система решается быстрее, чем обыкновенно, так как в некоторых уравнениях уже исключены те или другие неизвестные. Надо только сообразить, какие неизвестные и из каких уравнений следует исключить, чтобы возможно скорее дойти до одного уравнения с одним неизвестным. В нашем примере, исключив z из 1-го и 3-го уравнений и v из 2-го и 1-го, получим 2 уравнения с х и у:
Решив эти уравнения, найдем: х = 0, y = 1/3 . Теперь вставим эти числа во 2-е и 3-е уравнения; тогда получим: v = 3/2 ; z = 16/9 = 1 7/9 150. Случай, когда неизвестные входят в виде дробей: 1/x ; 1/y . . . Пусть дана, напр., система:
Всего проще такую систему можно решить посредством введения вспомогательных неизвестных. Положим, что 1/x = x', 1/y = y' 1/z = z', . Тогда мы получим такую систему с неизвестными х ', у' и z'
Решив эту систему, найдем:
Отсюда окончательно находим: x =2, y = 1, z = 3 Возьмем еще другой пример:
Дроби 3/x ; 2/y и т. п. можно рассматривать как произведения: 3 • 1/x ; 2 • 1/y и т. д. Поэтому, если положим, что 1/x = x', 1/y = y', и 1/z = z' , то система изобразится так:
Из этих уравнений находим: x' = 2, y' = 1/2, z' = 5 ; значит: 1/x = 2, 1/y = 1/2 , 1/z = 5 откуда: x = 1/2 , y = 2 , z = 1/5 ; 151. Случай, когда полезно все данные уравнения сложить. Пусть имеем, напр., систему:
Сложив все три уравнения, найдем:
Вычтя из последнего уравнения каждое из данных, получим:
___________________ |