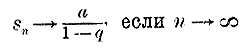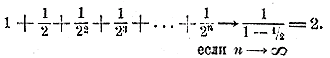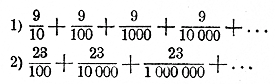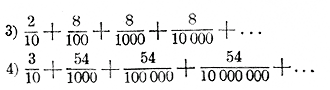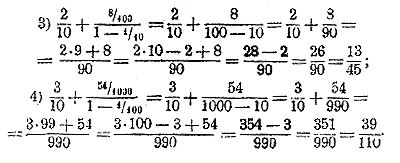| АЛГЕБРА В НАЧАЛО | ||||
|
ОТДЕЛ ДЕСЯТЫЙ. ПРОГРЕССИИ. Глава первая. Арифметическая прогрессия. Глава первая. Арифметическая прогрессия. 239. Задача. Рабочему поручили выкопать колодезь и условились платить ему за первый метр глубины 60 коп., за второй — 75 коп. и т. д., увеличивая плату за каждый следующий метр на 15 коп. Сколько уплатили рабочему, если колодезь был вырыт им в 10 метров глубины? Для решения задачи надо найти сумму чисел таких: 60 + 75 + 90 + 105 + 120 + 135 + 150 + 165 + 180 + 195. Сумму эту мы можем найти проще, чем обыкновенным сложением. Обозначив ее буквою s, напишем две такие строки: s = 60 +75 +90 +105 + 120 + 135 + 150+165 + 180 + 195, Вторую строку мы написали, переставив слагаемые первой строки в обратном порядке, отчего,конечно, сумма не изменилась. Сложим теперь все числа, стоящие друг под другом: 2s = 255 + 255 + 255 + 255 + 255 + 255 + 255 + 255 + 255 + 255, т. е. 2s =255•10 = 2550, и следовательно, s = 2550/2 = 1275 Таким образом, за всю работу пришлось заплатить 12 р. 75 к В этой задаче нам пришлось иметь дело с рядом чисел, последовательно возрастающих на одно и то же число. Подобные ряды носят особое название „прогрессий". Рассмотрим их подробнее. 240. Определение. Арифметической прогрессией называется такой ряд чисел, в котором каждое число, начиная со второго, равняется предыдущему, сложенному с одним и тем же постоянным для этою ряда числом (положительным или отрицательным). Так, два ряда чисел: 10, 14, 18, 22, 26, 30, 34, 38, 42, 46, 6, 4, 2, 0, — 2, — 4, — 6 составляют арифметические прогрессии, так как в них каждое число, начиная со второго, равно предыдущему числу, сложенному в первом ряду с положительным числом 4, а во втором с отрицательным числом — 2. Числа, составляющие прогрессию, называются ее членами; их число может быть произвольное. Положительное или отрицательное число, которое надо прибавить к предыдущему члену, чтобы получить последующий, называется разностью прогресcии. Прогрессия называется возрастающей или убывающей, смотря по тому, увеличиваются ли ее члены по мере удаления, от начала ряда, или уменьшаются; разность возрастающей прогрессии есть число положительное, а убывающей — отрицательное. Для обозначения того, что ряд представляет собою арифметическую прогрессию, иногда ставят в начале ряда знак ÷ . Обыкновенно принято обозначать: первый член а, последний l, разность d, число всех членов n и сумму их s. Ради краткости слова „арифметическая прогрессия" мы будем сокращенно писать так: А. П. 241. Формула любого члена арифметической прогрессии. Пусть имеем прогрессию: ÷ 10, 14, 18, ... (разность 4). Тогда 2-й член = 10 + 4 = 14; 3-й „ = 10 + 4 + 4 = 10 + 4•2=18; 4-й ,, =10 + 4 + 4 + 4 = 10 + 4•3 = 22. и т. д. Значит: 10-й член = 10 + 4•9 = 46; 20-й „ = 10 + 4•l9 = 86, и т. д. Подобно этому, если имеем прогрессию: ÷ 6, 4, 2, . . . (разность — 2), то 2-й член = 6 + (—2) = 4; 3-й „ = 6 + (—2) + (—2) = 6 + (—2) •2 = 2 и т.д. Напр.: 10-й член = 6 + (—2)•9 = — 12, и т. д. Вообще, если прогрессия будет такая: ÷ а, b, с, ... (разность d), то 2-й. член = a + d 3-й „ = a + d + d = a + 2d; 4-й „ = a + 2d + d = a + 3d, и т. д. Значит, 10-й член окажется a + 9d, 15-й член будет a + 14d, вообще m-й член будет Всякий член A. II., начиная со второго, равен первому ее члену, сложенному с произведением разности прогрессии на число всех членов, стоящих перед определяемым членом. В частности, последний член равен первому члену, сложенному с произведением разности на число всех членов, уменьшенное на 1, т. е. l = a + d(n — 1) Примеры. 1) Найти 10-й член прогрессии: ÷ 60, 75, 90,... Так как разность этой прогрессии равна 15, то 10-й член будет 60 + 15•9 = 195 (см, задачу § 239). 2) Найти 12-й член прогрессии: ÷ 40, 37, 34, ... Так как разность здесь равна — 3, то 12-й член должен быть: 40 + (—3) • 11 = 40 — 33 = 7. 3) Какое будет n-ое число в последовательном ряду нечетных чисел: 1, 3, 5,. . .? Такое число должно быть: 1+ 2 (n —1) =1 + 2n — 2 = 2n — 1. Следствие. А. П., у которой первый член есть а, разность d и число членов n, может быть изображена так: а, а + d, а + 2d, а + 3d, ... а + d(n— 1). 242. Формула суммы всех членов арифметической прогрессии. Предварительно убедимся в следующем свойстве: сумма двух членов A. П., равноотстоящих от концов ее, равна сумме крайних. Напр., в прогрессии: ÷ 3, 7, 11, 15, 19, 23, находим: 3 + 23 = 26; 7 + 19 = 26; 11 + 15 = 26. Понятно, почему это так: первые слагаемые этих сумм (т. е. 3, 7, 11) идут, все возрастая на 4, а вторые слагаемые (29, 19, 15) идут, все убывая на 4; поэтому сумма их не изменяется. Возьмем еще пример убывающей прогрессии: ÷ 8, 6, 4, 2, 0,—2,—4. В ней: 8 + (—4) = 4, 6 + (—2) = 4, 4 + 0 = 4. Член 2, отстоящий одинаково от начала и от конца, должен быть сложен сам с собою: 2 + 2 = 4. И здесь объяснение то же самое: слагаемые 8, 6, 4, 2 идут, все уменьшаясь на 2, а слагаемые — 4, — 2, 0 и 2 идут, все увеличиваясь на 2; от этого сумма их остается без изменения. Теперь выведем формулу для суммы всех членов любой А. П. Для этого применим тот способ, посредством которого мы нашли сумму членов А. П. в задаче § 239, а именно: сложим почленно два таких равенства: s = a + b + с +...+ i + k + l s = l + k + i +...+ c + b + a ______________________________________________ 2s = (a + l)+(b+ k) + (c + i)+...+(i + c) + (k + b) + (l + a). Hо a + l = b + k = с + i = ... = l + а; следовательно, 2s = (a + l) n, откуда
т. е. сумма всех членов А. II. равна половине произведения суммы крайних членов на число всех членов. Таким образом, в задаче § 239 для суммы s по этой формуле найдем: s = [(60 + 195) • 10]:2 = 2550:2 = 1275. Пример 1. Найти сумму натуральных чисел от 1 до n включительно. Ряд: 1, 2, 3, ...n есть А. П., у которой первый член 1, разность 1, число членов n и последний член тоже n ; поэтому
Пример 2. Найти сумму первых n нечетных чисел. Как мы видели в предыдущем параграфе, n-ое нечетное число равно 2n —1; поэтому:
Так: l + 3= 4 = 22; 1 + 3 + 5 = 9 = 32; l + 3+ 5 + 7 = 16 = 42, и т. д.
l + 3= 22; 1 + 3 + 5 = 32; l + 3+ 5 + 7 = 42, и т. д. Пример 3. Найти сумму 10 членов прогрессии: ÷ 3, 21/2, 2, ... Здесь a = 3, d = 21/2 — 3 = 1/2;
Поверка: 3 + 21/2+ 2 + 11/2 + 1 + 1/2 + 0 — 1/2 — 1 — 11/2 = 71/2 243. Замечание. Так как для 5 чисел a, l, d, n и s мы имеем два уравнения:
то по данным трем из этих чисел можем находить остальные два. Для примера решим следующую задачу: Найти число членов прогрессии, у которой первый член 7, разность — 2 и сумма всех членов 12. В этой задаче даны: а = 7, d = — 2 и s =12; остаются неизвестными l и n. Подставив в уравнение заданные числа, находим:
Получаются два ответа: число членов или 6, или 2. И действительно, две прогрессии: 7, 5, 3, 1 — 1, — 3 и 7, 5 имеют одну и ту же сумму 12. 244. Формула суммы квадратов чисел натурального ряда. При решении некоторых математических вопросов приходится пользоваться не только формулою, определяющею сумму чисел натурального ряда, но и формулой, определяющей сумму квадратов этих чисел. Формулу эту можно вывести следующим образом: Возьмем n таких числовых тождеств (отдел 2 глава 3 § 61, г): 23 = (1 + 1)3= 13 + 3 • 12• 1+ 3 • 1 • 12 + 13 33 = (2 + 1 )3 = 23 + 3 • 22• 1+ 3 • 2 • 12 + 13 43 = (3 + 1 )3 = 33 + 3 • 32• 1+ 3 • 3 • 12 + 13 ........................................................................ (n + 1)3 = n3 + 3n2• 1+ 3n • 12 + 13. Сложим все эти тождества. Тогда 23, стоящее в левой части первого равенства, взаимно уничтожится с 23, стоящим в правой части второго равенства, 33 в левой части второго равенства уничтожится с 33 в правой части- третьего равенства, и т. д. После такого уничтожения получим: (n + 1)3= 1 + 3 (12 + 22 + 32... + n2) + 3(1 + 2 + 3.. . + n) + n. Обозначив для краткости: 1 + 2 + 3.. . + n= S1, 12 + 22 + 32... + n2 = S2, мы будем иметь; (n + 1)3 =1+3S1 + 3S2 + n,
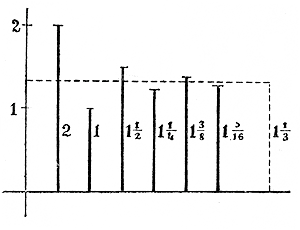
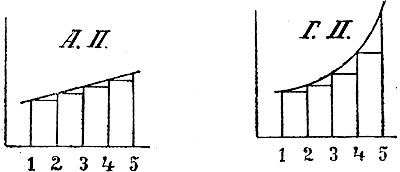
Геометрическая прогрессия. 245. Задача. Говорят, что индийский принц Сирам предложил изобретателю шахматной игры просить у него награды, какую он хочет. Тот попросил, чтобы ему дали за первый квадрат шахматной доски 1 пшеничное зерно, за второй квадрат 2 зерна, за третий 4 и т. д., увеличивая вдвое за каждый из следующих квадратов. Принц согласился. Но когда подсчитали количество пшеницы, которое следует выдать за все 64 квадрата шахматной доски, то оказалось, что награда в этом размере не может быть выдана по недостатку пшеницы. Сколько же зерен пришлось бы выдать изобретателю? Количество зерен, которое надлежало бы выдать за все 64 квадрата, равно сумме s следующего ряда чисел: 2s = 1 + 2 + 22 + 23 +... + 262 + 263. Мы можем найти эту сумму так: умножим обе части написанного равенства на 2: 2s = 2 + 22 + 23 + 24 +... + 263 + 264 Теперь вычтем из этого равенства предыдущее; тогда получим: s = 264—1. Значит, придется вычислить степень 264, что можно сделать или последовательным умножением на 2 по формуле: 264 = 2 • 2 • 2 • 2. .. (64 множителя) или по формуле: 264 = [(216)2]2 = (65 5362)2; окончательное число зерен будет: s = 264—1 = 18 446 744 073 709 551 615. Можно вычислить, что если бы такое число зерен рассыпать равномерно по всей земной суше, то образовался бы слои пшеницы толщиною около 9 мм. В этой задаче мы имеем дело с рядом чисел, из которых каждое, начиная со второго, равно предыдущему числу, умноженному на одно и то же число. Такие ряды чисел называются геометрическими прогрессиями. Рассмотрим их подробнее. 246. Определение. Геометрической прогрессией называется такой ряд чисел, в котором каждое число, начиная со второго, равняется предшествуюгцему, умноженному на одно и то же число, постоянное для этого ряда. Так три ряда: 2, 4, 8, 16, 32, 64, 128,...; 8, —16, 32, —64, 128, —256, 512; 20, 10, 5, 5/2, 5/4, 5/8, 5/16, 5/32 составляют геометрические прогрессии, потому что в этих рядах каждое число, начиная со второго, получается из предшествующего умножением: в первом ряду на 2, во втором на —2 и в третьем на 1/2, Для обозначения того, что данный ряд есть прогрессия геометрическая, иногда ставят в начале его знак - Как и в арифметической прогрессии, числа, составляющие геометрическую прогрессию называются ее членами; число,на которое надо умножить предыдущий член, чтобы получить последующий, называется знаменателем прогрессии. Прогрессия называется возрастающею или убывающею, смотря по тому, увеличивается или уменьшается абсолютная величина членов прогрессии по мере удаления от начала ряда; так, из трех указанных выше прогрессий первая и вторая — возрастающая, а третья — убывающая. В возрастающей прогрессии абсолютная величина знаменателя больше 1, в убывающей она меньше 1. Обыкновенно знаменатель прогрессии обозначают буквою q, а члены, число их и сумму обозначают так же, как это принято для арифметической прогрессии, т. е. а, b, с, ... l (последний член), n (число членов) и s (сумма). Для краткости слова „геометрическая прогрессия" мы будем сокращенно писать так: Г. П. 247. Сравнение Г. П. с А. П. Разность двух рядом стоящих членов в А. П. остается одна и та же, вследствие чего члены ее возрастают или убывают равномерно. Посмотрим, какова будет разность двух соседних членов в Г. П.: - Из определения прогрессии следует: b = аq, с = bq, d = cq и т. д.; следовательно: b — а = аq — а = а (q—1); с — b = bq — b = b(q—1), и т. д. Если прогрессия возрастающая и члены ее положительные, то тогда a < b < c < ... и т. д.; поэтому и а (q—1) < b(q—1) < c(q—1) <..., т. e. b — a < c — b < d — c < ... и т. д. Значит, в возрастающей Г. П. с положительными членами разность двух соседних членов увеличивается по мере удаления их от начала ряда; вследствие этого члены такой прогрессии, по мере их удаления от начала ряда, возрастают все быстрее и быстрее, что наглядно изображено на чертеже (правом).
Напр. ÷ 2, 4, 6, 8, 10, 12,... - 248. Формула любого члена Г. П. Пусть мы имеем такую Г. II. - Тогда 2-й член = 3•2 = 6; 3-й „ =3• 2•2 = 3•22=12; 4-й „ = 3•2•2•2 = 3•23 = 24, и т.д. Напр., 10-й член = 3•29 = 3•512 =1536, и т. д. Подобно этому, если мы имеем прогрессию: - то 2-й член = 10•1/2 = 5; 3-й „ 10•1/2•1/2 =10 • (1/2 )2 = 10/4 = 2 1/2; 4-й „ 10•1/2•1/2 •1/2=10 • (1/2 )3 = 10/8 = 1 1/4 и т. д.; Возьмем теперь прогрессию в буквенном виде: - Согласно определению Г. П., находим: 2-й член = aq = aq1; 3 „ „ = aq • q = aq2; 4 „ „ = aq2• q = aq3, и т.д. Таким образом, 10-й член = aq9, вообще m-й член = aq m-1 . Значит: всякий член Г. П., начиная со второго, равен первому члену, умноженному на такую степень знаменателя, которой показатель есть число членов, предшествующих определяемому. 1) В частности, последний член l, которому предшествует n — 1 членов, выразится формулой: l = aq n - 1 Пример 1. Найти 6-й член прогрессии - Знаменатель такой прогрессии есть 12:3 = 4; поэтому 6-й член = 3•45 = 3072. Пример 2. Найти 10-й член прогрессии - Так как знаменатель этой прогрессии равен 10:20 = 1/2, то 10-й член равен
Замечание. Геометрическую прогрессию, у которой первый член есть а, знаменатель q и число всех членов n, можно изобразить так: - 249. Формула суммы всех членов Г. П. Применим тот прием, которым мы раньше (§ 245) нашли сумму 1 + 2 + 22 + 23 +... + 263 Умножим обе части равенства: s = a + b + с +... + k + l (1) на знаменатель q; тогда получим: sq = aq + bq + сq +... + kq + lq . Но aq = b, bq = c, сq = d, ..., kq = l ; следовательно, sq = b + с + d + ... + l + lq (2) Вычтя почленно из равенства (2) равенства (1), найдем: sq — s = lq — а, т. е. (q — 1) s = lq — а, откуда:
Значит, гумма всех членов Г. П. равна дроби, у которой числитель есть разность между произведением последнего члена на знаменатель Г. II. и первым членом ее, а знаменатель есть разность между знаменателем прогрессии и единицей. Замечание. Так как для прогрессии убывающей lq < а и q <1, то для такой прогрессии лучше придать формуле суммы иной вид, умножив числитель и знаменатель дроби на —1:
Пример. Найти сумму 8 членов прогрессии, у которой a = 1 и q = 1/3 . Тогда
и
250. Пример задачи на Г. П. Найти первый член а и последний l, если q = 3, n = 5 и s = 242. Сначала находим l по формуле l = aq n - 1 = а • 34 и затем эту величину и данные числа подставим в формулу для суммы:
откуда: a = 242:121 = 2. Теперь находим: l = 2 • 34 = 162. Поверка: 2 + 6 + 18 + 54 + 162 = 242. Бесконечные прогрессии. 251. Некоторые свойства таких прогрессий. Если ряд чисел, составляющих прогрессию, может быть продолжаем без конца, то прогрессия называется бесконечной. Рассмотрим некоторые свойства таких прогрессий. а) Возьмем бесконечную возрастающую A. П., у которой разность очень мала, напр, такую: ÷ 1; 1,01; 1,02; 1,03; 1,04,.,. Несмотря на то, что члены этой прогрессии, при удалении от начала ряда, растут очень медленно, они, однако, при достаточном удалении могут превзойти любое данное число, как бы велико оно ни было; напр., они могут сделаться больше 1 000 000. Действительно, для того, чтобы (n + 1)-й член такой прогрессии, равный сумме 1+ 0,01n, мог сделаться больше 1 000 000, достаточно для n взять такое большое число, которое удовлетворяло бы неравенству: 1 + 0,01n > 1 000 000 Из него находим:
Так как в бесконечной прогрессии число n может сделаться как угодно большим, то оно может сделаться больше 99 999 900; и тогда 1 + 0,01n сделается больше 1000 000. Рассуждение это можно повторить о всякой арифметической возрастающей бесконечной прогрессии; поэтому мы можем высказать такое общее заключение: член бесконечной возрастающей А. П., при достаточном его удалении от начала ряда, может превзойти любое данное число, как бы оно велико ни было. б) Возьмем теперь бесконечную возрастающую Г. П. с положительными членами, напр, такую: - и сравним ее с бесконечной А. П.: ÷ 1; 1,01; 1,02; 1,03;... (разность 0,01), у которой первые два члена одинаковы со взятой нами Г. П. Как мы видели раньше, члены Г. П. возрастают быстрее, чем члены А. П. Но член взятой нами А. П., при достаточном удалении от начала ряда, может превзойти любое число, например может сделаться больше 1000 000; значит, соответствующий член нашей Г. П. и подавно может сделаться больше всякого числа. Таким образом, член бесконечной возрастающей Г. П. (с положительными членами), при достаточном удалении его от начала ряда, может превзойти любое данное число. Свойство это применимо и к такой возрастающей Г. П., у которой члены, все или некоторые, отрицательные числа (например — 5, —10, —20,... или 5, —10, 20, —40,...); тогда надо только говорить не о самих членах, а об их абсолютной величине. в) Возьмем какой-нибудь пример бесконечной убывающей Г. П. с положительными членами, например такой:
Члены такой прогрессии при удалении их от начала ряда, конечно, уменьшаются, но могут ли они при этом сделаться меньше всякого данного положительного числа, например меньше 0,000001, это сразу не видно. Чтобы обнаружить это, возьмем вспомогательную прогрессию, члены которой обратны членам взятой нами прогрессии: 1, 2, 22, 23,... 2n,... (знаменатель 2). Прогрессия эта возрастающая, и потому, как мы сейчас видели, члены ее могут превзойти любое данное число; значит, они превзойдут и 1 000 000. Если же окажется, что 2n > 1 000 000, то тогда, очевидно:
Применим это рассуждение к какой-угодно бесконечной убывающей Г. П. (с положительными членами): - Чтобы показать, что член этой прогрессии, при достаточном удалении его от начала ряда, может сделаться меньше любого положительного числа N, возьмем вспомогательную Г. П.:
Прогрессия эта возрастающая, так как ее знаменатель >1. Но член возрастающей Г. П. может превзойти всякое данное число; следовательно, он превзойдет и число 1/N Поэтому при достаточно большом n будет удовлетворено неравенство:
Итак, член бесконечной убывающей Г. П., при достаточном удалении его от начала ряда, может сделаться меньше любого данного положительною числа. 252. Понятие о пределе. Положим, что в бесконечной убывающей геометрической прогрессии:
мы взяли 10 членов от начала; тогда последний (10-й) член будет (1/2)9, а сумма этих 10 членов (которую обозначим s10) будет:
Подобно этому, найдем:
Мы видим, что по мере увеличения числа членов сумма их приближается все более и более к 2. Так сумма sn+1 меньше 2 на дробь (1/2)n, а эта дробь, как мы видели, при достаточно большом n, делается меньшей любого данного положительного числа. Если какое-нибудь переменное число (в нашем примере сумма членов прогрессии), изменяясь, приближается все более и более к некоторому постоянному числу (в нашем примере к числу 2) так, что разность между этим числом и переменным делается меньшей любого данного положительного числа, как бы мало оно ни было, то это постоянное число называется пределом переменного2). Заметив это, мы можем сказать, что переменная сумма
при неограниченном возрастании n стремится к пределу 2, что на письме выражают так:
(стрелки заменяют собою слово „стремится"), или пишут так:
Здесь „пред." есть сокращенное слово „предел", а добавление внизу скобки: n = ∞ заменяет собою фразу: „когда n неограниченно увеличивается" (когда n стремится к ∞). Можно наглядно показать, что рассматриваемая сумма приближается неограниченно близко к 2.
Пусть отрезок АА1 =1 АВ=2. 253. Формула предела суммы убывающей. Если в бесконечной Г П.: - возьмем n членов от начала, то последний член будет aq n - 1, и сумма их будет:
Предположим, что n неограниченно увеличивается. Тогда число
Таким образом, при неограниченном увеличении числа членов убывающей Г. П. сумма их стремится к пределу, равному частному от деления первого члена прогрессии на избыток единицы над знаменателем прогрессии. Так:
Замечание. Это свойство принадлежит Г. П. и при отрицательном знаменателе. Например, предел суммы членов Г. П.: - у которой q = 1/2 и а = 2, равен:
254. Применение Г. П. к десятичным периодическим дробям. Возьмем следующие два примера десятичных периодических дробей (чистых, т. е. таких, у которых период начинается тотчас после запятой): 1) 0,999... и 2) 0,232323... Дроби эти представляют собою суммы:
Слагаемые этих сумм суть члены бесконечных убывающих Г. П., у которых знаменатели прогрессии: у первой 1/10 , y второй 1/1000 . Суммы эти стремятся к пределам, равным:
Из этих примеров видно, что чистая периодическая дробь равна такой обыкновенной дроби, у которой числитель есть период, а знаменатель цифра .9, повторенная столько раз, сколько цифр в периоде. Надо только иметь в виду, что в этой фразе слова: „чистая периодическая дробь" поставлены ради краткости; подробнее надо было бы сказать: предел, к которому стремится чистая периодическая дробь, когда число периодов возрастает, равен и т. д. Возьмем теперь два примера периодических дробей смешанных (т. е. таких, у которых период начинается не тотчас после запятой): 3) 0,2888... и 4) 0,3545454... Дроби эти можно представить в виде суммы:
Слагаемые этих сумм, начиная со второго, суть члены бесконечных убывающих Г. П.; в 3-й сумме знаменателем служит дробъ 1/10 в 4-й сумме —дробь 1/100 Поэтому пределы, к которым стремятся эти суммы, будут:
Из этих примеров видно, что смешанная периодическая дробь равна такой обыкновенной дроби, у которой числитель есть число, стоящее до второго периода, без числа, стоящего до первого периода, а знаменатель есть цифра 9, повторенная столько раз, сколько цифр в периоде, со столькими нулями на конце, сколько цифр между запятой и периодом. Здесь тоже надо сделать замечание, что разумеется не сама периодическая дробь, а предел, к которому она стремится. |
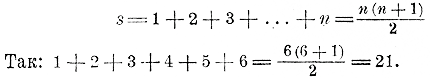
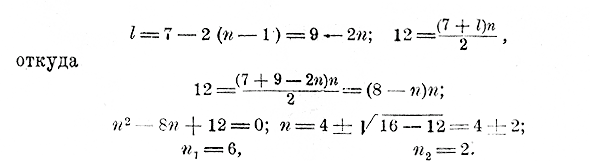
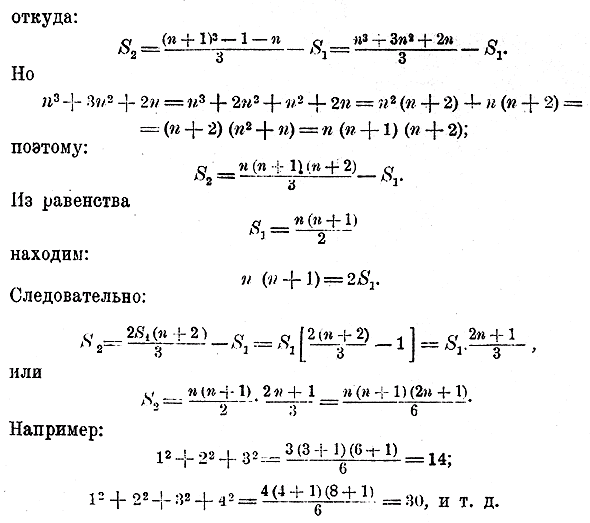
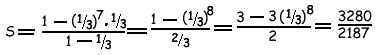
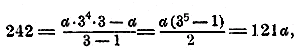
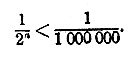
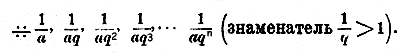
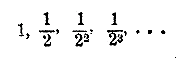
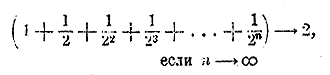
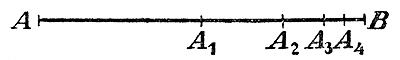
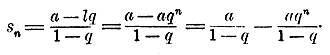
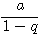остается неизменным, а дробь 
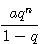все уменьшается, и притом неограниченно, так как числитель ее, как мы видели раньше, делается меньше любого данного положительного числа, а знаменатель остается неизменным. Значит:
