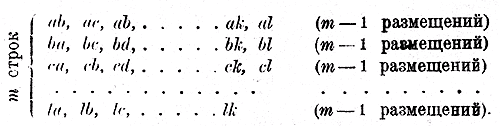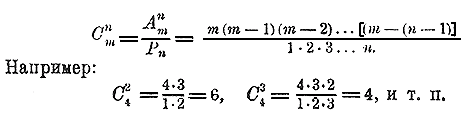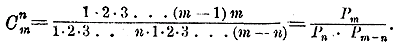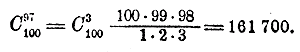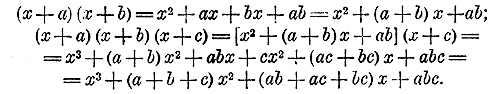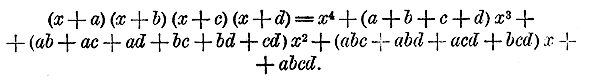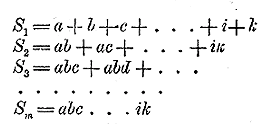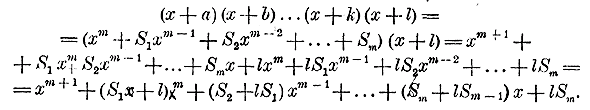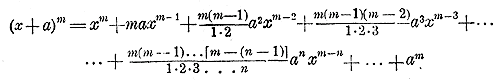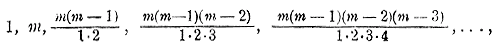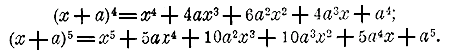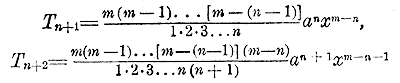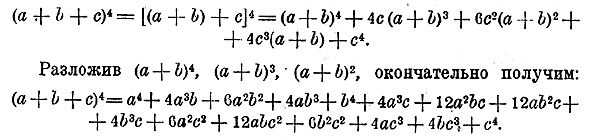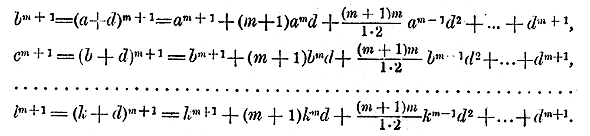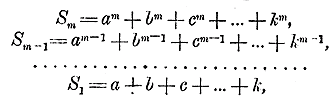| АЛГЕБРА В НАЧАЛО | ||||||
|
ОТДЕЛ ТРИНАДЦАТЫЙ. Соединения и бином Ньютона. Глава первая. Соединения. Глава первая. Соединения. 292. Определение. Различные группы, cоставленные из каких-либо предметов и отличающиеся одна от другой или порядком этих предметов или самими предметами, называются вообще соединениями. Если, например, из 10 различных цифр: 0,1, 2, 3,... 9 будем составлять группы по нескольку цифр в каждой, напр, такие: 123, 312, 8056, 5630, 42 и т. п., то будем получать различные соединения из этих цифр. Из них некоторые, напр. 123 и 312, различаются только порядком предметов, другие же, напр. 8050 и 312, разнятся самими предметами (и даже числом предметов). Предметы, из которых составляются соединения, называются элементами и обозначаются обыкновенно буквами а, b, с,... Соединения могут быть трех родов: размещения, перестановки и сочетания. Рассмотрим их отдельно. 293. Размещения. Пусть число предметов, из которых мы составляем различные соединения, равно 3 (напр, три карты); обозначим эти предметы а, b, и с. Из них можно составить соединения
Возьмем из этих соединений соединения по 2. Они отличаются одно от другого либо предметами, напр. аb и ас, либо порядком предметов, напр. аb и bа, но число предметов в них одно и то же. Такие соединения называются размещениями из 3 элементов по 2. Вообще размещениями из m элементов по n называются такие соединения, из которых каждое содержит n элементов, взятых из данных m элементов, и которые отличаются одно от другого или предметами или порядком предметов (значит, предполагается, что n < m). Так, написанные выше соединения по 3 будут размещены из 3-х элементов по 3 (различаются только порядком), соединения по 2 будут размещены из 3-х элементов по 2 (различаются или предметами или порядком). Размещения из данных m элементов могут быть по 1,по2, по 3,... и, наконец, по m. Иногда бывает нужно знать число всевозможных размещений, которые можно составить из m элементов по п, не составляя самих размещений. Число это принято обозначать так: Аnm (здесь A есть начальная буква французского слова „arrangement", что значит размещение). Чтобы найти это число, рассмотрим прием, посредством которого можно составлять всевозможные размещения. Пусть нам дано m элементов: а, b, с,... k, l. Сначала составим из них все размещения по одному. Их, очевидно, будет m. Значит: А1m = m. Теперь составим все размещение по два. Для этого к каждому из ранее составленных размещений по одному приставим последовательно все оставшиеся m — 1 элементов но одному. Так, к. элементу а приставим последовательно оставшиеся элементы: b, с,... k, l; к элементу b приставим последовательно оставшиеся элементы: a, с,... k, l и т. д. Тогда получим следующие размещения по два:
Так как всех элементов m, то из каждого размещения по 1 элементу мы получим m — 1 размещений по 2, а всего их будет (m — 1) m. Очевидно, что других размещений по 2 быть не может. Значит: А2m = m (m — 1). Чтобы составить теперь размещения по 3, берем каждое из составленных сейчас размещений по 2 и приставляем к нему последовательно по одному все m — 2 оставшихся элементов. Тогда получим следующие размещения по 3:
Так как число всех размещений по 2 равно m (m — 1) и из каждого получается (m — 2) размещения по 3, то всех таких размещений окажется: (m — 2) [m (m — 1)] = m (m — 1) (m — 2). Таким образом: А3m = m (m — 1)(m — 2). Подобно этому получим: А4m = m (m — 1)(m — 2)(m — 3); А5m = m (m — 1)(m — 2)(m — 3)(m — 4), и вообще: Аnm= m (m — 1)(m — 2) ... [m— (n— 1)]. Такова формула размещений; ее можно высказать так: число всевозможных размещений из m элементов по n равно произведению п последовательных целых чисел, из которых большее есть m. Таким образом: А24 = 4• 3 =12; А34 = 4• 3 • 2 = 24, А48= 8• 7• 6• 5 = 1680, и т. п. 294. Задачи. 1) В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в день? Всевозможные распределения уроков в день представляют собою, очевидно, всевозможные размещения из 10 элементов по 5; поэтому всех способов распределения должно быть: А510 = 10• 9 • 8• 7 • 6 = 30 210. 2) Сколько можно образовать целых чисел, из которых каждое выражалась бы тремя различными значащими цифрами? Искомое число есть число размещений из 9 значащих цифр по 3; следовательно, оно равно 9• 8• 7 = 504. 3) Сколько можно образовать целых чисел, из которых каждое выражалось бы тремя различными цифрами? Из 10 цифр: 0, 1, 2, 3, ... 9 можно составить размещений по три 10• 9• 8 = 720; но из этого числа надо исключить число тех размещений по три, которые начинаются с цифры 0. Таких размещений будет столько, сколько можно составить размещений по 2 из 9 значащих цифр, т. е. 9• 8 = 72; следовательно, искомое число 720 — 72 = 618. 295. Перестановки. Если размещения из m элементов взяты по n (и значит, различаются только порядком элементов), то такие размещения называются перестановками. Напр., перестановки из двух элементов а и b будут размещения из 2-х по 2, т. е. аb и bа, перестановки из 3-х элементов будут размещены из 3-х по 3, т. е. аbс, aсb, bас, bca, cab, сbа, и т. п. Число всевозможных перестановок из m элементов обозначается Рm (здесь Р есть начальная буква французского слова „permulation", что значит: перестановка). Так как перестановки из m элементов — это размещения из m по m, то формула перестановок будет такая: Рm = Аmm = m (m — 1)(m — 2) ... 3 • 2 • 1 = 1 • 2 • 3 ... (m — 1) m, т. е. число всевозможных перестановок из m элементов равно произведению натуральных чисел от 1 до m. 296. Задачи. 1) Сколько девятизначных чисел можно написать девятью разными значащими цифрами? Искомое число есть Р9 = 1 • 2 • 3 ... 9 = 362 880. 2) Сколькими способами можно разместить 12 лиц за столом, на котором поставлено 12 приборов? Число способов = 1•2•3 ... 12 = 479 001 600. Замечание. Произведение натуральных чисел от 1 до m включительно (обозначается сокращенно так: m ! ) растет чрезвычайно быстро с возрастанием m; так, при m = 12 оно дает 479 001600, при m = 100 оно выражается числом, требующим 158 цифр для своего изображения. 297. Сочетания. Если из всех размещений, которые можно составить из m элементов по n, мы отберем только те, которые одно от другого разнятся, по крайней мере, одним элементом, то получим размещения, которые называются сочетаниями. Напр., из 4 элементов а, b, с и d, сочетания по 3 будут: abc, аbd, acd, bcd. Если в каждом из этих сочетаний сделаем всевозможные перестановки, то получим всевозможные размещeния из 4-х элементов по 3.
Число таких размещений равно, очевидно, 6•4 = 24. Таким образом, число всех размещений из m элементов по n равно числу всех сочетаний из m элементов по n, умноженному на число всех перестановок, какие можно сделать из n элементов, т. е. Аnm = C nm Рn где C nm означает число всех сочетаний из m по n (С есть начальная буква французского слова "combinaison" , что значит: сочетание). Отсюда выводим следующую формулу сочетаний:
298. Задачи. 1) Из 10 кандидатов на одну и ту же должность должны быть выбраны трое. Сколько может быть разных случаев выборов? Искомое число, очевидно, составляет число всевозможных сочетаний из 10 элементов по 3, т. е.
2) Сколькими способами можно выбрать 13 карт из колоды в 52 карты? Искомое число представляет собою число сочетаний из 52 по 13, т. е.
299. Другой вид формулы сочетаний. Формулу сочетаний можно привести к другому виду, если умножим числитель и знаменатель ее на произведение 1•2•3...(m — n); тогда в числителе получим произведение: m(m — n) ... [m — (n— 1)] • 1•2•3 ... (m — n), которое, переставив сомножители, можно написать так: 1•2•3 ... (m — n) [m — (n— 1)] ... m. Следовательно,
300.Свойство сочетаний. Заменив в этой формуле n на m — n, получим:
Сравнивая эту формулу с предыдущей, находим: C nm = C m - nm К этому выводу приводит и такое простое рассуждение: если из m элементов отберем какие-нибудь n, чтобы составить из них одно сочетание, то совокупность оставшихся элементов составит одно сочетание из m — n элементов. Таким образом, каждому сочетанию из n элементов соответствует одно сочетание из m — n элементов, и наоборот; значит: C nm = C m - nm Это соотношение позволяет упростить нахождение числя сочетаний из m элементов по n, когда n превосходит 1/2 m, Например:
Бином Ньютона. 301. Произведение биномов, отличающихся только вторыми членами. Обыкновенным умножением находим:
Подобно этому найдем:
Рассматривая эти произведения, замечаем, что все они составлены по одному и тому же закону, а именно: Произведение составляет многочлен, расположенный по убывающим степеням буквы х. Показатель первого члена равен числу перемножаемых биномов; показатели при х в следующих членах постепенно убывают на 1; последний член не содержит х (содержит его в нулевой степени). Коэффициент первого члена есть 1; коэффициент второго члена есть сумма всех вторых членов перемножаемых биномов; коэффициент третьего члена есть сумма всех произведений вторых членов, взятых по два; коэффициент четвертого члена есть сумма всех произведений вторых членов, взятых по три. Последний член есть произведение всех вторых членов. Докажем, что этот закон применим к произведению какого угодно числа биномов. Для этого предварительно убедимся, что если он верен для произведения m биномов: (х + а) (х + b) (х + с) ... (х + k) , то будет верен и для произведения (m +1) биномов: (х + а) (х + b) (х + с) ... ( х + k )( х + l ). Итак, допустим, что верно следующее равенство: (х + а) (х + b) (х + с) ... (х + k) = хm + S1хm - 1+ S2хm - 2 +...+ Sm где
Умножим обе части этого равенства на новый бином x + l
Рассматривая это новое произведение, убеждаемся, что оно подчиняется такому же закону, какой мы предположили верным для m биномов. Действительно, во-первых, этому закону следуют показатели буквы х; во-вторых, ему же следуют и коэффициенты, так как коэффициент 2-го числа S1 + l есть сумма всех вторых членов перемножаемых биномов, включая сюда и l, коэффициент 3-го члена S2 + lS1 есть сумма парных произведений всех вторых членов, включая сюда и l, и т. д.; наконец lSm есть произведение всех вторых членов: а, b, с,... k, l. Мы видели, что закон этот верен для 4 биномов; следовательно, по доказанному теперь, он должен быть верен для 4 + 1, т. е. для 5 биномов; если же он верен для 5 биномов, то он верен и для 5 +1, т. е. для 6 биномов, и т. д. Изложенное рассуждение представляет так называемое "доказательство от m к m +1". Оно называется также „математической индукцией" (или „совершенной индукцией"). Заметим, что в предыдущих главах этой книги неоднократно представлялся случай применить доказательство от m к m +1 (напр, при выводе формулы любого члена прогрессии, Отдел 10 глава1 § 241, глава 2 §248 и др.). Мы этого не делали только ради простоты изложения. 302. Формула бинома Ньютона. Предположим, что в доказанном нами равенстве: (х + а) (х + b) ... (х + k) = хm + S1хm - 1+ S2хm - 2 +...+ Sm все вторые члены биномов одинаковы, т. е. что a = b = с = ...= k. Тогда левая часть будет степень бинома (х + а)m. Посмотрим, во что обратятся коэффициенты S1 ,S2 , . . . Sm. Коэффициент S1 равный а + b + с + ... + k, обратится в ma, Коэффициент S2, равный аb + ас + ad + ..., обратится в число a2, повторенное столько раз, сколько можно составить сочетаний из m элементов по 2, т. е. он обратится в
Это равенство известно как формула бинома Ньютона1), причем многочлен, стоящий в правой части формулы, называется разложением бинома. Рассмотрим особенности этого многочлена. 303. Свойства бинома Ньютона. Этих свойств мы укажем следующие 10: 1) Показатели буквы х постепенно уменьшаются на 1 от первого члена к последнему, причем в первом члене показатель х равен показателю степени бинома, а в последнем он есть 0; наоборот, показатели буквы а постепенно увеличиваются на 1 от первого члена к последнему, причем в первом члене показатель при а есть 0, а в последнем он равен показателю степени бинома. Вследствие этого сумма показателей при x и а в каждом члене одна и та же, а именно: она равна показателю степени бинома. 2) Число всех членов разложения есть m +1, так. как разложение содержит все степени а от 0 до m включительно. 3) Коэффициенты равны: у первого члена 1, у 2-го члена — показателю степени бинома, у 3-го члена —числу сочетаний из m элементов по 2, у 4-го члена —числу сочетаний из m элементов по 3; вообще коэффициент (n + l)-гo члена есть число сочетаний из m элементов по n. Наконец, коэффициент последнего члена равен числу сочетаний из m элементов по m, т. е. 1. Заметим, что все эти коэффициенты называются биномиальными. 4) Обозначая каждый член разложения буквою Т с цифрою внизу, указывающею номер места этого члена в разложении, т. е. первый член T1 второй член T2 и т. д., мы можем напиcать:
Эта формула выражает общий член разложения, так как из нее можем получить все члены (кроме первого), подставляя на место n числа: 1, 2, 3,. . .m. 5) Коэффициент 1-го члена от начала разложения равен 1, коэффициент 1- го члена от конца тоже равен 1. Коэффициент второго члена от начала есть m, т. е. C 1m коэффициент 2-го члена от конца есть C m - 1m, но так как C 1m = C m - 1m , то эти коэффициенты одинаковы. Коэффициент 3-го члена от начала есть C 2m, а 3-го члена от конца есть C m - 2m; но C 2m = C m - 2m поэтому и эти коэффициенты одинаковы, и т. д. Значит, коэффициенты членов, одинаково удаленных от концов разложения, равны между собою. 6) Рассматривая биномиальные коэффициенты:
мы замечаем, что при переходе от одного коэффициента к следующему числители умножаются на числа все меньшие и меньшие (на m—1, на m—2, на m— 3 и т. д.), а знаменатели умножаются на числа все большие и большие (на 2, на 3, на 4 и т. д.). Вследствие этого коэффициенты сначала возрастают (пока множители в числителе остаются бoльшими соответственных множителей в знаменателе), а затем убывают. Так как коэффициенты членов, равноотстоящих от концов разложения, одинаковы, то наибольший коэффициент должен находиться посредине разложения. При этом, если число всех членов разложения нечетное (что бывает при четном показателе бинома), то по средине будет один член с наибольшим коэффициентом; если же число всех членов четное (что бывает при нечетном показателе бинома), то посредине должны быть 2 члена с одинаковыми наибольшими коэффициентами. Например.
7) Из сравнения двух рядом стоящих членов:
видно, что для получения коэффициента следующего члена достаточно умножить коэффициент предыдущего члена на показатель буквы х в этом члене и разделить на число членов, пред шествующих определяемому. Пользуясь этим свойством, можно сразу писать, напр.: (х + а)7 = х7 + 7ах6... Теперь берем 7, умножаем его на 6 b делим на два, получаем 21: (х + а)7 = х7 + 7ах6 + 21a2x5... Теперь берем 21, умножаем на 5 и делим на 3, получаем 35: (х + а)7 = х7 + 7ах6 + 21a2x5 + 35a3x4 Теперь уже выписаны члены до середины ряда, остальные получим, основываясь на свойстве 5-м: (х + а)7 = х7 + 7ах6 + 21a2x5 + 35a3x4 + 35a4x3 + 21a5x2 + 7а6 х+ а7 8) Сумма всех биномиальных коэффициентов равна 2m. Действительно, положив в формуле бинома x = а = 1, получим:
Напр., сумма коэффициентов в разложении (х + а)7 равна: 1 + 7 + 21 + 35 + 35 + 21 + 7 + 1 = 128 = 27. 9) Заменив в формуле бинома а на — а, получим:
и следовательно, знаки + и — чередуются: 10) Если в последнем равенстве положим x = а =1, то найдем:
т. е. сумма биномиальных коэффициентов, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах. 304. Применение формулы бинома к многочлену. Формула бинома Ньютона позволяет возвышать в степень трехчлен и вообще многочлен. Так:
305. Сумма одинаковых степеней членов арифметической прогрессии. Укажем одно из интересных применений формулы бинома. Пусть имеем арифметическую прогрессию, содержащую n + 1 членов: ÷ а, b, с,... k, l. Если разность ее d, то b = а + d, c = b + d,... l = k + d. Возвысив эти равенства по формуле бинома Ньютона в m + 1 степень, получим n следующих равенств:
Сложив эти равенства и положив для краткости:
получим (члены: bm+1... k m+1 сократятся):
Из этого уравнения определим Sm, если известны Sm - 1 , Sm - 2 ,...S1. Полагая последовательно m = 1, 2, 3,..., найдем S1 потом S2 затем S3 и т. д. 306. Сумма одинаковых степеней чисел натурального ряда. Применив выведенное в предыдущем параграфе уравнение к прогрессии: ÷ 1, 2, 3, 4,... n, n +1, получим:
|