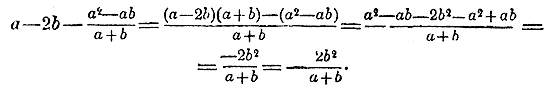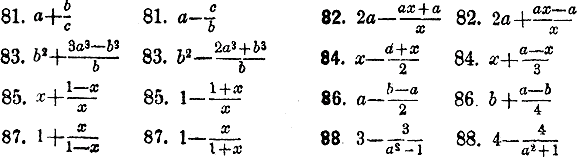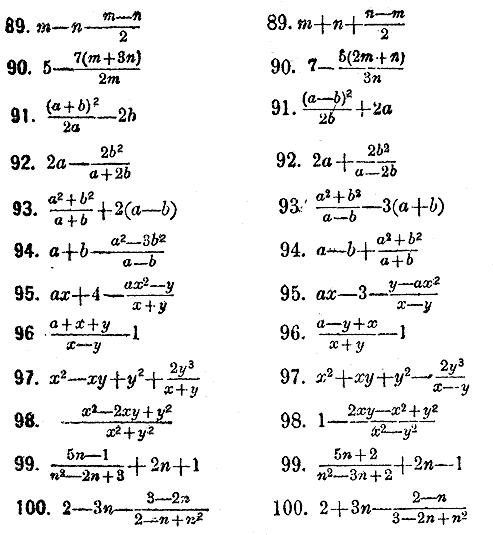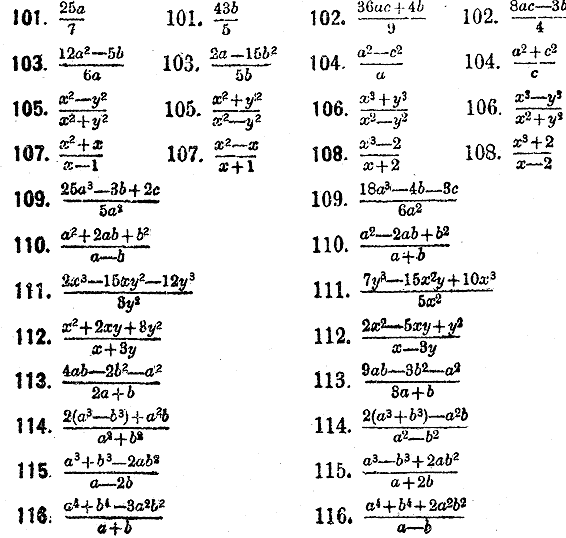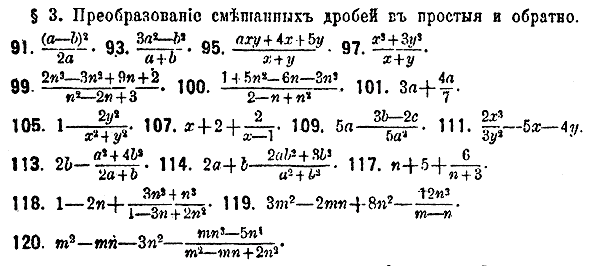|
ОТДЕЛЕНИЕ V. ПРЕОБРАЗОВАНИЕ ДРОБНЫХ ВЫРАЖЕНИЙ . § 3. Преобразование смешанных дробей в простые и обратно. Если данное дробное выражение представляет только частное от деления числителя на знаменатель и не содержит целого слагаемаго или вычитаемаго, то оно называется простой или одночленной дробью. Таково, напр., представияеть сумму или разноть дроби с целым выражением, то оно называется смешанной или многочленной дробью. Напр., Смешанную дробь можно всегда преобразовать в простую. Для этого нужно умножить целое выражение на знаменатель дроби, приложить к произведению или вычесть из него (смотря по знаку, стоящему перед дробью) числитель ядроби и весь полученный результат сделать числителем новой дроби, а знаменателяь подписать прежний. В более сложных случаях следует сначала только обозначить действия, не производя их сразу во избежание возможной ошибки. Приводим пример, наглядно указывающий рекомендуемый порядок вычислений:
Простые дроби также иногда обращают в смешанные. Обыкновенно это делают только в тех случаях, когда целое выражение выделяется непосредственно при делении числителя на знаменателя. Тогда именно нужно разделить числитель на знаменатель и к полученному целому частному приложить дробь, числитель которой есть остаток деления, а знаменатель прежний. Подобное преобразование полезно иногда делать для облегчения сокращения дроби, так как, отделяя целое выражение, мы часто получаем дробь более простого состава, а свойство сократимости ее всегда такове же, как и у данной дроби. Напр., подобное обстоятельство обнаруживается в следующем примере:
Здесь числитель и знаменатель данной дроби довольно трудно преобразовываются в произведения, а после выделенил целого слагаемого общий множитель a—b обнаруживается легко. Преобразовать следующиe смешанныe дроби в простыe:
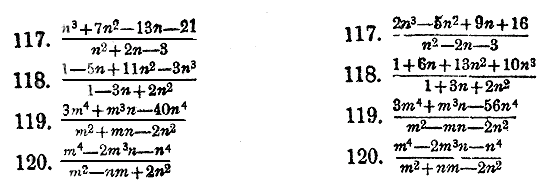
Преобразовать нижеследующие простые дроби в смешанные:
|
. Если же данное выражение
есть смешанная дробь.
