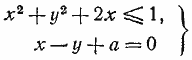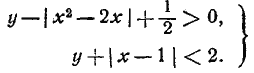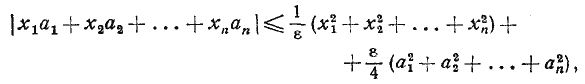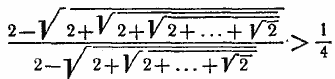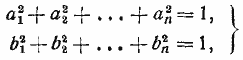ГЛАВА  5

НЕРАВЕНСТВА

585.  Найти все   действительные  значения r, при которых многочлен

(r²— 1)х² + 2(r — 1)х + 1

положителен для всех действительных х.   Решение

586.  Доказать, что выражение

неотрицательно при любых вещественных х и у, не равных нулю.Решение

587.  При каких значениях а система неравенств

удовлетворяется для всех значений x?Решение

588.  Доказать, что для   любых   действительных чисел а, b, с, d справедливо неравенство

а⁴ + b⁴ + с⁴ + d ⁴> 4abcd;

Решение

589. Найти все значения а, при которых смешанная система

имеет единственное решение. Найти соответствующие решения.Решение

590.  Найти  пары  целых чисел х и у, удовлетворяющие системе неравенств

Решение

591. Показать, что при всяком целом п > 1  справедливо неравенство

Решение

592.Доказать, что при всяком  целом положительном т справедливо неравенство

Решение

593. Показать, что при любом натуральном n

Решение

594.Доказать, что при   п > 2

(п!)² > п^п.

Решение

595. Доказать, что из трех  отрезков с длинами   а > 0, b > 0,   с > 0 можно построить треугольник тогда и только тогда, когда

pa² + qb² > pqc²

для любых чисел р и q, связанных соотношением

р + q = 1

Решение

596. Доказать,   что  при   любых   вещественных   х,  у,  z  имеет место   неравенство

4х (х + у) (х + z) (х + у + z) + у²z²  > 0.

Решение

597. Доказать, что при любых вещественных х и у имеет место неравенство

х² + 2ху + 3у² + 2х + 6y + 4 > 1.

Решение

598. Доказать, что при условии 2х + 4у =1  выполняется неравенство

х² + у²  >  ¹/₂₀

 Решение

599. Каким условиям должно удовлетворять число   d > 0 для того, чтобы при R > r > 0 имело место неравенство

Решение

600. Доказать неравенство

(а, b, с положительны).Решение

601. Доказать, что если а, b, с — числа одного знака и а < b < с, то,

а³(b² — с²) + b³(с² — а²) + с³(а² —b²) < 0.

 Решение

602. Доказать, что если  a₁, a₂, a₃, ..., a_n положительны и a₁a₂a₃, ...a_n = 1,  то

(1 + a₁) (l + a₂) (1 +a₃).. .(1 + a_n)  > 2^п.

Решение

603. Доказать, что если а + b = 1, то

а⁴ + b⁴ >¹/₈.

 Решение

604. Доказать, что многочлен

x⁸ — x⁵ + x²— x + 1

положителен при всех вещественных x.   Решение

605. Доказать, что  если   |x| <1,   то при любом целом n  >2 выполняется неравенство

(1 —x)^п + (1 + x)^п < 2^п.

Решение

606.  Доказать,   что

где x₁, x₂,  ..., x_n  , a₁, a₂,  ..., a_n и ε — произвольные вещественные числа, причем ε > 0.

Решение

607.При каких действительных значениях x  выполняется неравенство

 Решение

608. Доказать, что   при   всех   положительных   х  и  у и целых положительных m и n  (n > m) имеет место неравенство:

 Решение

609. Доказать неравенство

.

 Решение

610.Доказать неравенство

при условии, что числитель левой части неравенства содержит п знаков радикала, а знаменатель содержит п—1 знак. Решение

611. Доказать,   что    для   любых    вещественных   чисел a₁, a₂,  ..., a_n и b₁, b₂,  ..., b_n, удовлетворяющих соотношениям

справедливо неравенство

| a₁b₁ + a₂b₂ + ... + a_nb_n | < 1.

 Решение

612. Доказать,  что  если   числа   x₁, x₂,  ..., x_n   положительны и удовлетворяют соотношению

x₁, x₂,  ..., x_n  = 1, то

x₁+ x₂ +  ...+ x_n    > n

 Решение