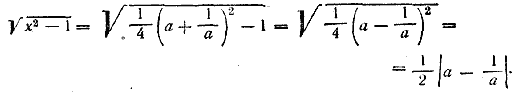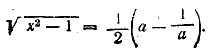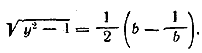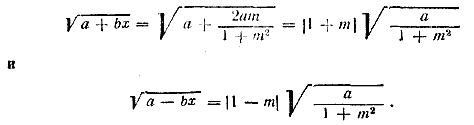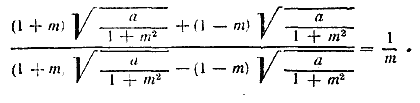|
|
ГЛАВА 2 АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ Ответы и решения 72. Числитель преобразуется к виду а2—b2, знаменатель — к виду а+b. Ответ. а — b. Замечание. Чтобы корни были арифметическими, числа а и b не должны быть отрицательными. ____________________________________________________________________
Ответ b(а3—b3) Замечание. Предполагается, что а > b (иначе первый корень не будет арифметическим) __________________________________________________________________ 74. В этом примере величина, стоящая под знаком кубического радикала, всегда отрицательна. Действительно, выражения √16x и √2x (они имеют действительные значения лишь при х > 0) мы должны считать положительными (иначе выражение Итак, под знаком кубического корня стоит отрицательное число. Поэтому и сам кубический корень имеет отрицательное значение! Выполним такое преобразование:
Теперь радикал, стоящий в правой части, является арифметическим корнем. После приведения к одному показателю с первым из данных сомножителей получаем
Перемножая корни, получаем: Ответ Замечание. Если не обратить внимания на отрицательность выражения под знаком кубического корня, то получится неверный ответ ___________________________________________________________________ 75. Первый радикал равен (a+1) за знак радикала, получаем
Приведем радикалы к одному показателю:
Если число а+1 положительно, то |а+1|=а+1, и по сокращении получаем . Замечание. Число а+1 и будет положительным. Действительно, так как подкоренное выражение (а+1)4 (а—1) предполагается положительным (или равным нулю), а множитель (а+1)4 ни в каком случае не может быть отрицательным, то а—1>0, т. е. а >1, а при этом условии а+1>2. Ответ. __________________________________________________________ 76. Считая все корни арифметическими, приведем сомножители
к одинаковому показателю 6. Первый и второй сомножители примут соответственно вид
Перемножив их, получим Замечание. Первый сомножитель является арифметическим корнем только при условии а>0 (при а<0 подкоренное выражение отрицательно, при а=0 оно теряет смысл). Второй же сомножитель является арифметическим корнем при любом значении а (крoме а= — 1). Следовательно, величине а можно давать любые положительные значения. Ответ. _________________________________________________________________ 77. Введем ab под знак первого радикала. Данное выражение примет вид
Замечание. Чтобы данные радикалы были арифметическими корнями, должно быть а> b. Случай а = b исключается, так как второй сомножитель теряет смысл. Ответ. 1. ___________________________________________________________________ 78. Освобождаемся от иррациональности в знаменателях; получим (√6 — 11) (√6 + 11) = —115. Ответ — 115. ___________________________________________________________ 79. Делимое равно Замечание. Чтобы все данные корни были арифметическими, должны одновременно удовлетворяться три условия: а>0, а—b>0, а+b>0 (их можно заменить двумя условиями: а>0, |b|<|а|, Отв. __________________________________________________________ 80 Делимое равно Отв. 2/3 ' ___________________________________________________ 81. Числитель первой дроби приводится к виду
Если выражения 1+ а и 1 —а оба положительны, то (см. предварительные замечания, п. 3) числитель равен Замечание. Чтобы радикалы, входящие в данное выражение были арифметическими корнями, нужно, чтобы величины 1+а и 1 — а имели одинаковые знаки. Но невозможно, чтобы обе они были отрицательны, так как 1+а<0 при условии а< — 1 и 1—а<0 при условии а>1, а эти условия несовместны. Для того же, чтобы величины 1+а и 1—а были обе положительны, нужно, чтобы выполнялось условие —1<а<1, т. е. чтобы было |а|<1 (значения а = ±1 исключаются,
так как при каждом, из них одно из данных выражений Отв. 0. ___________________________________________________ 82.Подставив
Так как по условию а>1, то а— 1/а >0. Поэтому Точно так же найдем Подставляем найденные значения радикалов в данное выражение, Ответ
_______________________________________________ 83.Подставляя
Так как величина 1+m2 всегда положительна, то и величина а должна быть положительной (при а<0 оба корня мнимы, при а=0 они равны нулю, и данное выражение неопределенно). Так как, согласно дополнительному условию, |m|< l, то обе величины 1+т и 1—т положительны. Данное выражение принимает вид
Oтвет. 1/m (При a>0). ___________________________________________________________ |
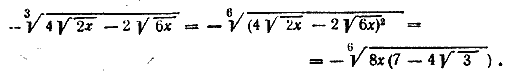
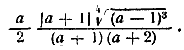
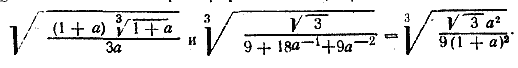
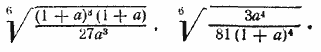 '
'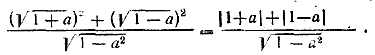
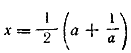 в выражение
в выражение