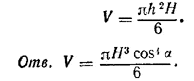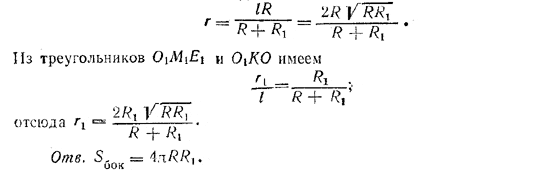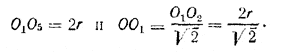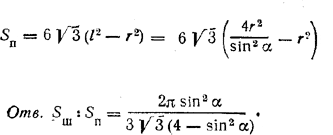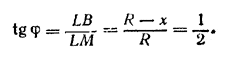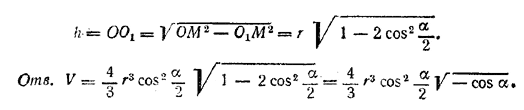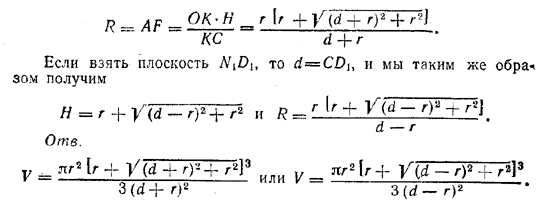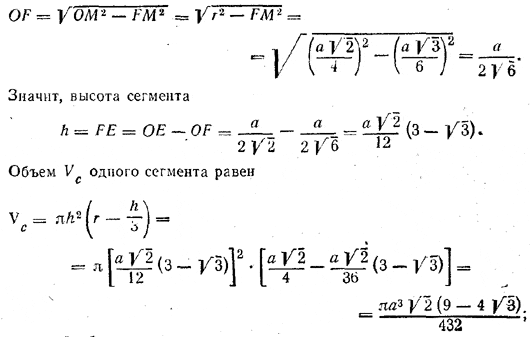ГЛАВА   3

КРУГЛЫЕ ТЕЛА

Ответы и решения

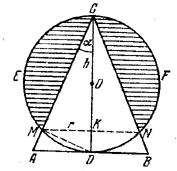
262. На рис. 233 осевое сечение той части шара, объем которой требуется определить, обозначено штриховкой.

рис. 233

Этот объем V получается вычитанием объема V₁ конуса MCN из объема V₂ шарового сегмента   CEMKNF.   Введем   обозначения:   МК= r   и   KC = h.   Так как радиус шара равен  OC = ¹/₂CD = ^H/₂, то

Сюда нужно подставить выражения

h =MC • cos α = H cos² α     и     r = MC • sin α = H cos α sin α 

(вычисление упростится, если предварительно заменить r²=МК² через
CK • KD = h (H — h)); тогда

______________________________________________

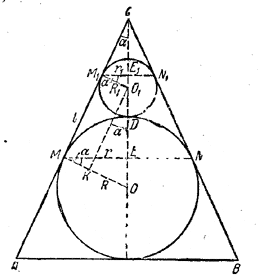
263. При обозначениях рис. 234 имеем: S_бок.  = π (r + r₁)l.

рис. 234

Проведем радиусы OM = R и О₁M₁ = R₁ в точки, касания и прямую O₁K, перпендикулярную к ОМ. Получим треугольники О₁M₁E₁, ОМЕ и O₁КО, которые подобны друг другу (как прямоугольные, имеющие по равному углу α). В А О₁КО имеем

О₁О = R + R₁;        OK = R — R₁;         O₁K = MM₁ = l .

Следовательно,

Из   подобных   треугольников   ОМЕ   и   O₁KO   имеем отсюда

______________________________________________

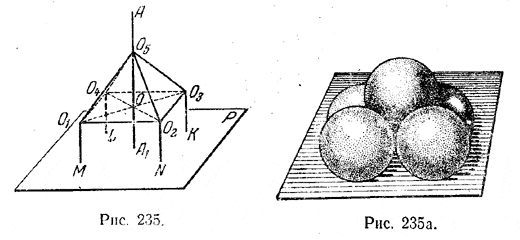
264. На плоскости Р (рис. 235)  лежат четыре шара радиуса r; М, N, К и L — точки их касания с плоскостью Р.

Их центры О₁,О₂,О₃,О₄ удалены от плоскости на расстояния О₁М=O₂N=O₃K=O₄L= r. Расстояние между центрами двух касающихся друг друга шаров равно 2r, т. е.
О₁О₂=О₂О₃=О₃О₄=О₄О₁ = 2r. Пятый шар касается каждого  из четырех    первых;    следовательно,   центр  его О₅ удален от центров О₁ О₂, О₃, О₄ также на расстояние 2r ,т.е. O₁O₅=O₂О₅=О₃О₅=О₄О₅=2r. Поэтому фигура О₅О₁О₂О₃О₄ будет правильная четырехугольная пирамида, у которой все ребра равны (как при основании, так и боковые). Центр пятого шара будет удален от плоскости Р на расстояние, равное OO₅+ ОА₁ = ОО₅+r. Верхняя точка А пятого шара будет находиться на продолжении перпендикуляра А₁О₅ на расстоянии О₅А= r от центра O₅. Таким образом, расстояние АА₁ от верхней точки пятого шара до плоскости Р равно 2r + ОО₅. Отрезок ОО₅ находим из прямоугольного треугольника O₁OO₅, где

Отв. AA₁ = r (2 + √2 ).

______________________________________________

265. Центры О₁,О₂,О₃,О₄ четырех шаров, должны   находиться .на расстоянии 2r друг от друга  (см. предыдущую задачу). Значит, фигура О₁О₂О₃О₄ — правильный тетраэдр с ребром 2r. Конус АСВ (рис. 236) , описанный около четырех шаров, касается одного из них O₄ по окружности NT, а каждого из трех остальных (например шара O₁) в двух точках: одна из них, К, лежит на основании, другая, М — на боковой поверхности.

Ось конуса совпадает с высотой O₄O тетраэдра. Центр O₁ лежит в плоскости осевого сечения ACD, проходящего через точку касания М (ибо прямая О₁М перпендикулярна к общей касательной плоскости конуса и шара, а плоскость осевого сечения ACD перпендикулярна к этой касательной плоскости). Значит, плоскость ACD пересекает шар О₁ по большому кругу; шар О₄ она пересекает тоже по большому кругу, и образующая АС  есть  общая  касательная   этих  больших  кругов.

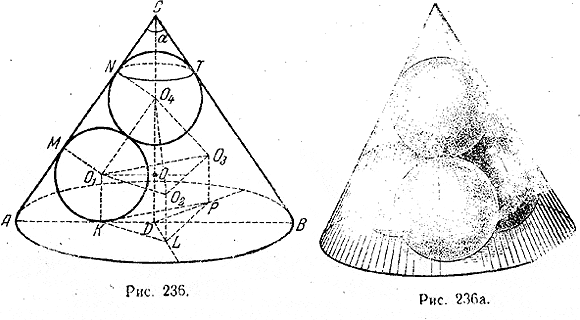
Следовательно,  AC || O₁O₄    и  /  O₁O₄O = /  ACD= ^α/₂ (α — искомый угол при вершине  С осевого   сечения).    Значит,

Но O₁O₄ = 2r,  а  отрезок OO₁  (радиус  круга, описанного около треугольника O₁O₂O₃)   равен    Получаем sin ^α/₂= ¹/_√3

Отсюда можно найти cos α = cos^{2   α}/₂ —  sin^{2   α}/₂ = ¹/₃.

Отв. α = 2 arc sin ¹/_√3   = arc cos ¹/₃

______________________________________________

266. Плоскость, делящая  пополам  двугранный угол   при   ребре A₁A₂ (рис. 237) усеченной пирамиды, проходит через высоту O₁O₂ и перпендикулярна к грани В₁С₁С₂В₂   (доказать!).   

Аналогично для двух других боковых ребер.    Поэтому   центр   шара,   касающегося граней пирамиды, лежит на высоте (а именно, на середине  высоты, так как шар касается и оснований),  а   точка К касания    шара с гранью В₁С₁С₂В₂ лежит на апофеме D₁D₂ этой грани. Аналогично для других боковых граней. Имеем

(a₁ = B₁C₁  и  а₂ = В₂С₂ — стороны  оснований  и  l =D₁D₂— апофема боковой грани).   Если r₁ = O₁D₁    и    r₂=О₂D₂ — радиусы    кругов, вписанных   в  основания,    то      a₁ = 2r₁√3  и a₂ = 2r₂√3 .   Поэтому

S_п.  = 3 √3 (r₁² + r₂²) + 3 √3 (r₁ + r₂) l

Как в задаче 242, найдем, что r₁ + r₂ = l   и   r₁² + r₂² = l² — 2r².

Тогда получим

______________________________________________

267. Обозначим радиус  OL  цилиндра (рис. 238) через х, а   радиус ОВ  основания    конуса через  R.

Так   как    по условию ML=R, то полная поверхность цилиндра S_п. =2πх² + 2πхR. По   условию

2πх² + 2πхR = ³/₂πR²  или   х²+ Rx — ³/₄ R² = 0  

откуда х = ^R/₂.   (отрицательное    решение   х = — ³/₂R не годится). Из треугольника LMB находим

Отв. φ = arctg ¹/₂.

______________________________________________

268. Центр О вписанного шара (рис. 239) лежит на высоте пирамиды, а точки касания К, L, М, N шара с боковыми гранями лежат на апофемах ЕК₁, EL₁, EM₁, EN₁ (ср. задачу 266). Четырехугольник KLMN — квадрат, являющийся основанием пирамиды, объем которой требуется определить.

рис. 239

Проведем через радиусы ОМ и ON плоскость NOM. Она будет перпендикулярна к грани ВЕС (так как проходит через прямую ОМ, перпендикулярную к плоскости ВЕС), а также к грани DEC (так как проходит через ON). Следовательно, плоскость NOM перпендикулярна к ребру ЕС.

Пусть Р — точка пересечения плоскости NOM с ребром ЕС. Тогда угол NPM есть линейный угол двугранного угла α. В четырехугольнике OMPN два угла (при вершинах М и N) прямые. Следовательно, /  NОМ =180° — α  .  Значит,

Из треугольника ОО₁М, где О₁M =  ^a/_√2  находим

______________________________________________

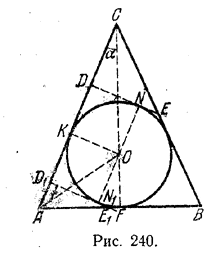
269. Можно провести две плоскости,   перпендикулярные  к данной образующей конуса (СА на рис. 240) и касающиеся вписанного шара; их точки касания (N и N₁) лежат на диаметре NN₁ параллельном СА.

Положим сначала, что берется плоскость ND, касающаяся шарa в точке N. Четырехугольник ONDK (К — точка касания образующей СА с шаром) — квадрат, так что DK=ON= r. По условию CD = d. Следовательно, CK= d + r. Из треугольника КОС находим

СО = √(d + r)² + r².

Следовательно,

Н = CF = OF + ОС = r + √(d + r)² + r² .

Из подобия треугольников   AFC и KОС находим

AF : Н = ОК : КС,

откуда

______________________________________________

270. Центр О шара (рис. 241)  лежит на диагонали АВ. Действительно, точка О одинаково удалена от граней AA₁N₁N и AA₁Q₁Q. Значит, она лежит на плоскости, делящей пополам двугранный угол при ребре   АА₁. Таким же  образом точка О должна  лежать на плоскости, делящей пополам двугранный угол при ребре AN. А эти две плоскости пересекаются по диагонали АВ.

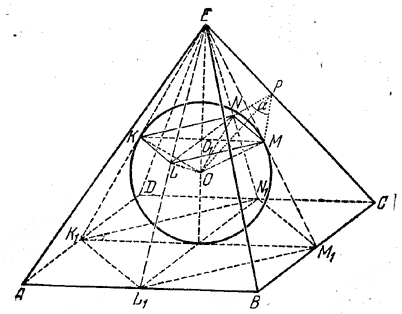
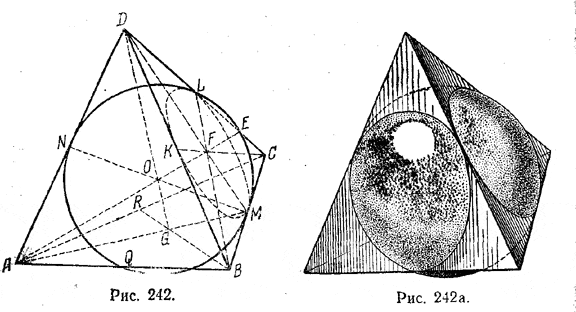
Пусть С и D — точки касания шара с гранями ANUQ и AA₁N₁N, а r — радиус шара. Тогда OC=OD= r, и плоскость ODGC перпендикулярна к ребру AN, а также к ребру BQ₁

Так как ребро SQ₁ по условию касается шара, то плоскость ODGC пересечет ребро в точке Е его касания с шаром; следовательно, ОЕ= r. С другой стороны, точка Е есть вершина квадрата FGКЕ, получаемого в сечении куба плоскостью ODGC; значит четырехугольник MOLE (OL и ОМ — продолжения   прямых   ОС и OD) — квадрат.    Следовательно, ОМ = ^r/_√2.   Так    как  OM + ОD = MD = a, то ^r/_√2 + r = а, откуда r = (2 — √2 ) а.

Часть поверхности сферы, лежащая вне куба, состоит из трех равных сегментов, один из которых есть EZTL. Поверхность этого сегмента равна

2πr • LZ = 2πr (CZ — CL) =2πr (2r — а),

Отв. r = (2 — √2 ) а;    S = 6πa² (10 — 7√2).

______________________________________________

271. Центр шара, касающегося ребер тетраэдра ABCQ (рис. 242), совпадает с центром тетраэдра (т. е. с точкой О, равноотстоящей от вершим А, В, С, D), а точки касания шара с ребрами суть середины ребер. Например, точка касания N есть середина ребра AD. Действительно, все шесть равнобедренных треугольников АОВ, ВОС, СОА, BOD, COD и AOD (начерчен только треугольник AOD) равны друг другу (по трем сторонам). Следовательно, их высоты ОМ, ON и т. д. равны.  Поэтому, если описать шар радиусом ON = r, то он пройдет через середины L, М, N, Q, K, R ребер и там коснется их  (так как ON_|_AD и т, д.).

Проведем через высоту тетраэдра  DG  и  ребро AD плоскость ADG. Она   будет   перпендикулярна   к   ребру   ВС   (доказательство дано в задаче 143) и пересечет это ребро в его середине М. В сечении получим равнобедренный треугольник AMD (AM=MD). Проведем высоту MN этого треугольника (N — середина AD). Центр О лежит на MN (так как он равноудален от А и О). Следовательно, MO=NO. Значит, r = ^MN/₂. Высота MN определяется из треугольника    ANM,    где AN = ^a/₂ и  AM = ^a√3/₂.   (как апофема рaвностороннего треугольника ABC). Имеем

Часть шара, расположeнная вне тетраэдра, состоит из четырех равных сегментов, отсекаемых от шара гранями тетраэдрa. Рассмотрим одну из граней BDC. Круг LMK, лежащий в основании сегмента, вписан в равносторонний треугольник BDC (ибо стороны треугольника касаются шара; значит, они касаются и малого кругa LMK,  лежащего в плоскости BDC). Радиус     этого    круга FM = ^a√3/₆

Следовательно,

искомый объем

V  = 4V_c

Замечание. Круг LKM, вписанный в треугольник BCD. изображается эллипсом, который легко будет начертить от руки, если кроме точек К, L, М предварительно отметить еще три точки, соответственно симметричные с ними относительно F (точка F есть точка пересечения медиан треугольника BDC).

______________________________________________