Графики функций   у = tg x  и  у = ctg x

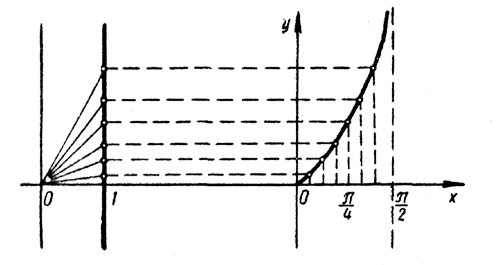
Схематично поведение функции у = tg x было представлено в разделе Изменение тригонометрических  функций. Теперь мы начертим точный график этой функции. Для этого исцользуем геометрическое построение, аналогичное тому, которое было описано в  для построения синусоиды . Мы не будем подробно останавливаться на этом построении, а ограничимся лишь тем, что приведем соответствующий рисунок . Учащиеся без особого труда   смогут   разобраться   в   нем   самостоятельно.

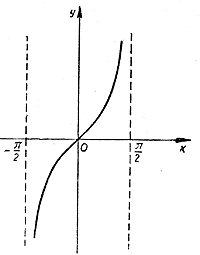
Теперь,   используя   график   функции   у = tg х в интервале 0 < х < ^π/₂   можно построить график этой функции и в интервале — ^π/₂ < х <0. Для этого  воспользуемся    тождеством

tg (—φ) = — tg φ.

Оно указывает на то, что график функции y = tg x симметричен относительно начала координат. Отсюда сразу же получается та часть графика,   которая   соответствует   значениям — ^π/₂ < х <0

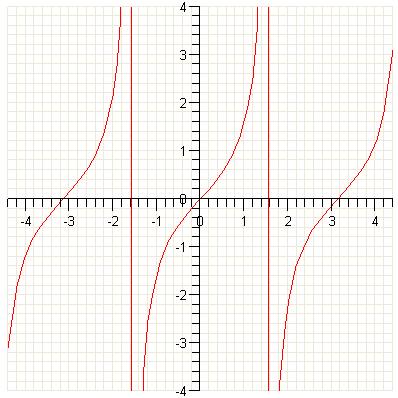
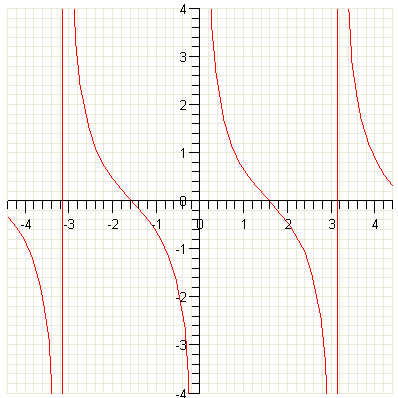
Функция y = tg x периодична с периодом π. Поэтому теперь для построения ее графика нам остается лишь продолжить периодически кривую, представленную на рисунке, влево и вправо с периодом   π. В результате получается кривая, которая называется тангенсоидой.

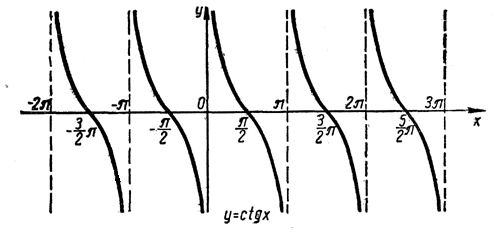
Тангенсоида хорошо иллюстрирует все те основные свойства функции у = tg x,   которые раньше были доказаны нами.   Напомним эти свойства.

1)  Функция у = tg x определена для всех, значений х,   кроме х = ^π/₂ + nπ, где n — любое целое число. Таким образом, областью ее определения служит совокупность всех действительных чисел, кроме х = ^π/₂ + nπ.

2)  Функция у = tg x   не ограничена.  Она  может принимать как  любые  положительные,   так  и  любые   отрицательные   значения. Следовательно, областью ее изменения является совокупность всех действительных чисел. Среди этих чисел нельзя указать ни наибольшего, ни наименьшего.

3)  Функция у = tg x  нечетна (тангенсоида симметрична относительно начала координат).

4)  Функция у = tg x периодична с периодом π.

5) В интервалах

nπ < х < ^π/₂ + nπ

функция  у = tg х положительна,  а в интервалах

—  ^π/₂ + nπ< х < nπ

отрицательна. При х = nπ функция у = tg x обращается в нуль Поэтому эти значения аргумента (0; ± π; ± 2π; ±3π; ..) служат нулями функции у = tg x.

6)  В  интервалах

—  ^π/₂ + nπ < х <  ^π/₂ + nπ 

функция монотонно возрастает. Можно сказать, что в любом интервале, в котором функция у = tg x определена, она является монотонно возрастающей.

Однако ошибочно было бы считать, что функция у = tg x монотонно возрастает всюду. Так, например ,    ^π/₄ + ^π/₂ > ^π/₂ .  Однако   tg (^π/₄ + ^π/₂) < tg ^π/_{4 .} Это   объясняется   тем,   что   в    интервал,   соединяющий точки х =^π/₄ и х = ^π/₄ + ^π/₂, попадает значение х = ^π/₂, при котором функция у = tg x не определена.

****************

Для построения графика функции у = ctg x следует воспользоваться   тождеством

ctg x = — tg (x + ^π/₂)

Оно указывает на следующий порядок построения графика:

1)  тангенсоиду у = tg x  нужно сдвинуть влево по оси абсцисс на расстояние ^π/₂;

2)  полученную кривую отобразить  симметрично относительно оси абсцисс.

В результате такого построения получается кривая, представленная на рисунке. Эту кривую иногда называют котангенсоидой.

Котангенсоида хорошо иллюстрирует все основные свойства функции у = ctg х. Предлагаем учащимся сформулировать эти свойства и дать им графическую интерпретацию.

Упражнения

1.Используя графики функций у = tg x и у = ctg х, найти наименьшие положительные корни уравнений:

a)  tg х = —3;   б)  tg х = 2;     в) ctg х = —3;    г) ctg x = 2.

2.  Используя графики функций у = tg x и у = ctg х, найти все  корни   уравнений:

a) tg х = \/3;   б) ctg x = ¹ / _{\/ 3}