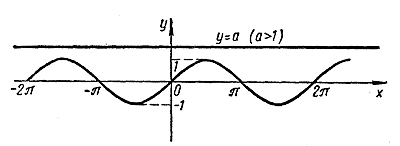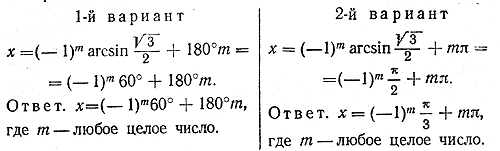| 3ГОНОМЕТРИЯ В НАЧАЛО | ||||||||||
|
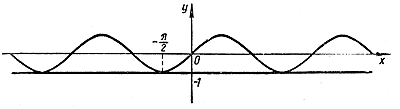
Уравнение sin х = а Каждый корень уравнения sin х = а (1) можно рассматривать как абсциссу некоторой точки пересечения синусоиды у = sin х с прямой у = а, и, наоборот, абсцисса каждой такой точки пересечения является одним из корней уравнения (1). При | а | >1 синусоида у = sin х не пересекается с прямой у = а . В этом случае уравнение (1) корней не имеет.
|
||||||||||
|
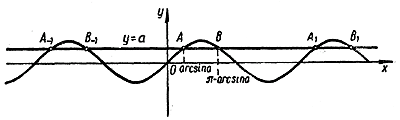
Если же | а | < 1, то синусоида у = sin х и прямая у = а имеют бесконечно много общих точек. В этом случае уравнение (1) имеет бесконечное множество корней. Пусть 0<а<1. Тогда в интервале 0< x < π имеем две точки пересечения: А и В.
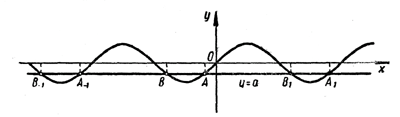
Точка А попадает в интервал — π/2 < x < π/2 . Поэтому ее абсцисса равна arcsin а. Чтоже касается точки В, то ее абсцисса, как легко понять из рисунка, равна π — arcsin а. Все остальные точки пересечения синусоиды у = sin х с прямой у = а мы разобьем на две группы: ... , A—2 , A — 1 , A 1 , A2 , ... , ... , B—2 , B — 1 , B 1 , B2 , ... , Точки первой группы удалены от А на расстояния, кратные 2π, и потому имеют абсциссы arcsin a + 2nπ, где n пробегает все целые числа (n = 0, ± 1, ± 2, ± 3, ...). Точки второй группы удалены от В на расстояния, кратные 2π , и потому имеют абсциссы π — arcsin а + 2kπ = —arcsin а + (2k + 1)π, где k пробегает все целые числа (k = 0, ± 1, ±2, ±3, ...). Таким образом, уравнение (1) имеет две группы корней: х = arcsin a + 2nπ (2) и х = —arcsin а + (2k + 1)π. (3) Легко понять, что обе эти группы корней можно представить одной формулой х = (—1)m arcsin a + mπ, (4) где т пробегает все целые числа (m = 0, ±1, ±,2, ±3, ...). Действительно, при m четном (m = 2n) (4) обращается в (2), а при m нечетном (m = 2k + 1) — в (3). Итак, при 0 < а < 1 все корни уравнения (1) задаются формулой (4). К такому же результату можно прийти и в случае —1< а < 0. Мы не будем подробно разбирать этот случай, предлагая учащимся сделать это самостоятельно с помощью рисунка.
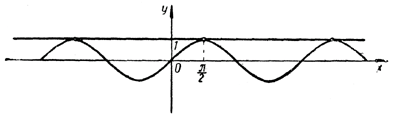
Нам осталось рассмотреть случай, когда а = 0 и а = ±1. При а = 0 уравнение sin x = а имеет корни х = mπ, (5) где m пробегает все целые числа (m = 0, ±1, ±2, ±3, ...). Такой же результат дает и формула (4) при а = 0. Действительно, arcsin 0 = 0 и потому (—1)m arcsin 0 + mπ = mπ Следовательно, формула (4) формально дает все корни уравнения (1) и в случае, когда а = 0. Если а =1, то корнями уравнения sin x = а будут числа х = π/2 + 2k π, (6) где k пробегает все целые числа (k = 0, ±1, ±2, ±3, ...).
Формула (4) охватывает и этот случай. Действительно, полагая в ней а = 1 и учитывая, что arcsin 1 = π/2, получаем: (— 1)m arcsin 1 + mπ = (— 1)m π/2 + mπ. Если m четно (m = 2k), то (— 1)m arcsin 1 + mπ = π/2 + 2kπ. Если же m нечетно (m = 2k + 1), то (— 1)m arcsin 1 + mπ = — π/2+ 2kπ + π = π/2+ 2kπ. И тот и другой случай учитываются формулой (6). Наконец, если а = —1, то корнями уравнения sin x = а будут числа: x = —π/2 + 2kπ, (7) где k пробегает все целые числа (k = 0, ±1, ±2, ±3, . . . ).
Предлагаем учащимся доказать, что при а = —1 формула (7) дает тот же результат, что и общая формула (4). Таким образом, формула (4) задаст все корни уравнения (1) при любых значениях а, если только | а | < 1. Однако при а = 0, а = +1 и а = —1 целесообразнее сразу же использовать формулы (5), (6) и (7), не обращаясь к общей формуле (4). В заключение отметим, что формулы (4), (5), (6) и (7) можно использовать лишь тогда, когда искомый угол х выражен в радианах. Если же х выражен в градусах, то эти формулы нужно естественным образом изменить. Например, вместо формулы (4) нужно использовать формулу х = (—1)m arcsin а + 180°m, вместо формулы (5) — формулу х = 180°m и т. д. Примеры. 1) Решить уравнение sin х = \/ 3/2 . Приведем два возможных варианта записи решения.
Недопустимо в одном и том же решении частично использовать 1-й и частично 2-й варианты. Например, ответ к данному упражнению нельзя записать в виде х = (—1)m 60° + mπ или х = (—1)m π/3 + 180°m 2) Решить уравнение sin ( l - 2x)= — 1/2 В отличие от примера 1, здесь искомые значения х нельзя выражать в градусах. В условии задачи под знаком синуса стоит выражение 1 — 2х. Наличие единицы указывает, что х — либо угол, выраженный в радианах, либо просто число. Поэтому решение данного уравнения нужно записать следующим образом: 1— 2x = (—1)m arcsin(— 1/2 ) + mπ = (—1)m arcsin(—π/6 ) + mπ = (—1)m+1arcsin(π/6) + mπ Отсюда x = 1/2 + (—1)m π/12 — π/2 m Например, при m = 0 x = 1/2 + π/12; при m = 1 x = 1/2 — π/12 — π/2 = 1/2 — 7π/12 и т. д. 3) Решить уравнение sin (30° — х) = 0. Здесь, как легко понять, под х подразумевается угол, выраженный в градусах. Поэтому решение данного уравнения нужно записать следующим образом: 30° — х = 180°m, х = 30° — 180°m. Поскольку под m мы подразумеваем любое целое число (в том числе и отрицательное), то полученный результат можно, конечно, представить и в другой форме, а именно: х = 30° + 180° n, где n — любое целое число. Упражнения Решить уравнения :
|