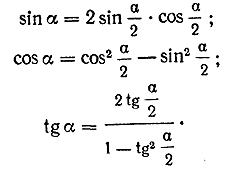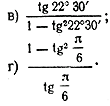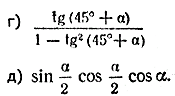Тригонометрические функции двойного угла

Положив в формуле

sin (α + β)  = sin α • cos β + sin β • cos α.

β = α,мы получим:

sin 2α = sin α • cos α + sin α • cos α = 2 sin α cos α.

Итак,

sin 2α = 2 sin α cos α         (1)

Синус двойного угла равен удвоенному произведению синуса данного угла на его косинус.

Аналогично, положив в формуле

cos (α + β) = cos α cos β — sin α sin β,  

β = α, получим::

cos 2α = cos α cos α—sin α sin α=  cos ² α — sin ² α.

Итак,

cos 2α = cos ² α — sin ² α.        (2)

Косинус двойного угла равен квадрату косинуса данного угла минус квадрат синуса того же угла.

Точно так же, положив в формуле

β = α, получим:

Тангенс двойного угла равен удвоенному тангенсу данного угла, деленному на единицу минус квадрат тангенса того же угла.

Примеры.   

1) Пусть sin α = 0,6, причем угол α оканчивается   во   2-й четверти.

Тогда cos α = — \/1 — sin² α =  — \/ 1 — 0,36 =  — 0,8.

Поэтому

sin 2α = 2 sin α • cos α = 2 • 0,6 • (— 0,8) = — 0,96;

cos 2α = cos ² α — sin ² α = 0,64 — 0,36 = 0,28.

2) Пусть tg α = 3.  Тогда

Замечание.   Не следует думать, что двойной угол  обязательно содержит четное число градусов или радианов: 20°;   60°; 4; 6 и т. д. Под двойным углом можно понимать любой угол. Например,

и т. д., вообще,  α = 2 • ^α/₂. Поэтому   иногда  доказанные   выше формулы полезно записывать в виде:

Эти формулы выражают тригонометрические  функции    угла через тригонометрические функции половинного угла.

Упражнения

1.  Известно, что sin α = 0,8, причем угол α  оканчивается во 2-й четверти.   Найти  синус,   косинус,   тангенс  и   котангенс угла 2α.

2.   Найти tg 2α и cos 2α, если известно, что угол α оканчивается не в 1-й четверти и
tg α = ⁴/₃.

3.   Найти cos α, еслц sin α = 0,1 и  угол α оканчивается в 4-й четверти.

4.  В какой четверти оканчивается угол α, если

а)  sin α > 0, sin 2α > 0;                 в) sin α < 0, sin 2α > 0;

б)  sin α > 0, sin 2α < 0;                 г) sin α < 0, sin 2α < 0?

5.   Вычислить:

а)  sin 22°30' • cos 22e30';

б)  cos² 22°30' — sin² 22°30';

6. Доказать тождества:

а)  (sin α + cos α)² = 1 + sin 2α;

б)  cos⁴ α — sin⁴ α = cos 2α;

в)  ctg α — tg α = 2 ctg ²α.

7.  Доказать, что для любого острого угла α

sin 2α < 2 sin α.

8.  В каких пределах может изменяться выражение sin α • cos α?

9. Упростить выражения:

a).  sin² ( β — 45°) — cos² ( β — 45°).

б). sin ( ^π/₄ — α ) • cos ( ^π/₄ — α )

в).

г). (sin ^α /₄ + cos ^α /₄ ) (sin ^α /₄ — cos ^α /₄)

10.Доказать равенства:

а). sin 10° • cos 20° • cos 40° = ¹ /₈.

б). sin ^π/₅ • cos ^2π/₅ = ¹/₄  tg ^π/₅

11. Выразить sin α и cos α:

а) через sin ^α /₂ и cos ^α /₂;

б)  через sin ^α /₂;

в)  через cos ^α /₂.

12. Упростить выражения:

а).

б).   (tg α + ctg α) sin 2α.

в).  2 cos² α — cos 2α

13. Вычислить:

а).  tg(2arctg3).

б).  tg [2arccos (—³/₅)],

в).  cos ( 2arcsin ¹/₂ )

г).  sin [2arctg ( —2)].

14. Найти  формулу  общего  членa   арифметической   прогрессии, для которой
а₁ = cos 2φ;   а₂ = cos ²φ

15. Доказать, что бесконечная геометрическая прогрессия, у которой  
а₁ = 4sin φ,  а₂ = sin 2φ, является бесконечно убывающей, и найти ее сумму.