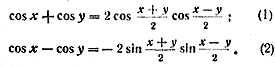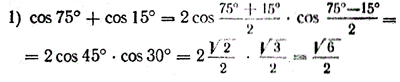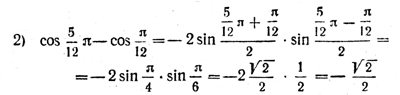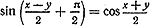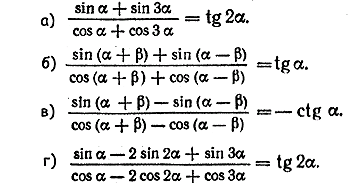| 3ГОНОМЕТРИЯ В НАЧАЛО |
|
Преобразование суммы (разности) косинусов двух углов в произведение Для суммы и разности косинусов двух углов верны следующие формулы:
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы на косинус полуразности этих углов. Разность косинусов двух углов равна минус удвоенному произведению синуса полусуммы на синус полуразности этих углов. Примеры
Формулы (1) и (2) могут быть получены многими способами. Докажем, например, формулу (1). 1-й способ. Ранее уже была доказана формула cos α cos β = 1/2 [cos (α + β) + cos (α — β)]. Полагая в ней (α + β) = х, (α — β) = у, мы и приходим к формуле (1). Этот способ аналогичен тому, с помощью которого в предыдущем параграфе была получена формула для суммы синусов двух углов. 2-й способ. В предыдущем параграфе была доказана формула
Полагая в ней α = х + π/2, β = у + π/2, получаем:
Но по формулам приведения sin ( х + π/2 ) == cos x , sin ( у + π/2 ) = cos у;
Следовательно,
что и требовалось доказать. Формулу (2) мы предлагаем учащимся доказать самостоятельно. Попробуйте найти не менее двух различных способов доказательства! Упражнения 1. Вычислить без таблиц, используя формулы для суммы и разности косинусов двух углов: а). cos 105° + cos 75°. г). cos 11π/12 — cos 5π/12.. б). cos 105° — cos 75°. д). cos 15° —sin 15°. в). cos 11π/12 + cos 5π/12.. е). sin π/12 + cos 11π/12. 2. Упростить данные выражения : а). cos (π/3 + α ) + cos ( π/3 — α ). б). cos (π/3 + α ) — cos ( π/3 — α ). 3. Каждое из тождеств sin α + cos α = \/2 sin (α + π/4) sin α — cos α = \/2 sin (α — π/4) доказать не менее чем двумя различными способами. 4. Данные выражения представить в виде произведений: а). \/2 + 2cos α. в). sin x + cos y. б). \/3 - 2 cos α. г). sin x — cos y. 5. Упростить выражение sin2 (α — π/8) — cos2(α + π/8) . 6.Разложить на множители данные выражения (№ 1156—1159): а). 1 + sin α — cos α б). sin α + sin (α + β) + sin β. в). cos α + cos 2α + cos 3α г). 1 + sin α + cos α 7. Доказать данные тождества
8. Доказать, что косинусы углов α и β равны тогда и только тогда, когда α = ± β + 2 nπ, где n — некоторое целое число. |
|
|