Глава III. Кривые второго порядка

§ 41. Исследование  гиперболы  по  ее  каноническому  уравнению

Рассмотрим гиперболу, заданную в некоторой прямоугольной декартовой системе координат своим каноническим уравнением

       (1)

Отметим следующие свойства гиперболы:

1) Гипербола (1) не имеет общих точек с осью Оу, a ось Ох пересекает в двух точках.

Для определения координат точек пересечения гиперболы (1) с осью Оу нужно решить совместно их уравнения

,     x = 0

Подставляя x = 0 в уравнение гиперболы, получим y² = — b², а это означает, что система не имеет решений. Следовательно, гипербола не пересекает ось ординат.

Для определения координат точек пересечения гиперболы (1) с осью Ох нужно решить совместно их уравнения

,     y = 0

Точка пересечения гиперболы с осью Ох должна иметь ординату у = 0 и в то же время принадлежать гиперболе. Подставив у = 0  в уравнение гиперболы, получим

х = ± а .

Итак, точками пересечения гиперболы (1) с осью Ох будут точки А(а; 0) и В(—а; 0); они называются вершинами гиперболы.

Отрезок АВ называется действительной осью гиперболы. Длина отрезка АВ, очевидно, равна 2а. Число а называют действительной полуосью гиперболы, число b - мнимой полуосью.

2) Гипербола имеет две взаимно перпендикулярные оси симметрии.

В уравнение (1) переменные х и у входят только во второй степени. Следовательно, если координаты точки N(х; у) удовлетворяют уравнению (1), то этому же уравнению будут удовлетворять и координаты точек N₁(—х; у) и N₂(x; —у).

Легко видеть, что точка N₁ симметрична точке N относительно оси ординат, точка N₂ симметрична точке N относительно оси абсцисс.

Таким образом, гипербола имеет две оси симметрии, oни взаимно перпендикулярны.

3) Гипербола имеет центр симметрии.

Если координаты точки N(x; у) удовлетворяют уравнению (1), то этому же уравнению удовлетворяют и координаты точки К(—х; —у). Точка К, очевидно,симметрична точке N относительно начала координат. Таким образом, гипербола имеет центр симметрии. Центр симметрии гиперболы называется центром гиперболы.

4) Гипербола (1) пересекается с прямой у = kx при | k |< ^b/_a в двух точках.
Если | k |> ^b/_a    , то общих точек у гиперболы и прямой нет.

Для определения координат точек пересечения гиперболы (1) и прямой у = kx нужно решить систему уравнений

          (2)

Исключая у, получаем

откуда

(b² — k²a²)x² = a²b².

При b² — k²a² < 0, т. е. при | k |> ^b/_a ,   полученное уравнение, а поэтому и система (2) решений не имеют. Следовательно, прямые, проходящие через начало координат с угловым коэффициентом, модуль которого больше или равен    ^b/_a   не пересекают гиперболу (1).   Прямые с уравнениями у = ^b/_a х и у = — ^b/_a х называются асимптотами гиперболы (1).

При b² — k²a² > 0, т. е. при | k |< ^b/_a система (2) имеет два решения:

Следовательно, каждая прямая, проходящая через начало координат с угловым коэффициентом, модуль которого меньше    ^b/_a  пересекает гиперболу (1) в двух точках
(рис. 114).

При k = 0 из формул (3) получаем х = ±а, у = 0, т. е. прямая у = 0 пересекает гиперболу в ее вершинах.

Так как гипербола симметрична относительно осей координат, то достаточно изучить ее форму в первом квадранте координатной плоскости. Из формул

        k > 0

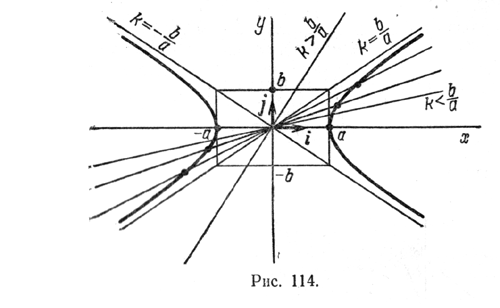
видно, что при возрастании й от нуля до ^b/_a  (при этом прямая у = kx поворачивается против движения часовой стрелки) и абсциссы и ординаты точек пересечения прямой с гиперболой возрастают. Прямая у = kx пересекaет гиперболу во все более далеких от начала координaт точках. Таким образом, гипербола (1) имеет вид, изображенный на рис. 114. Она состоит из двух не связанных между собой частей, называемых ее ветвями.

Замечание 1. Гиперболу  можно построить и теми методами, которые изучаются в алгебре и началах анализа. Для этого следует разрешить уравнение гиперболы относительно переменной у и построить графики функций

y = ^b/_a  √x² — a²   и   у = — ^b/_a  √x² — a².

Достаточно построить график одной из этих функций и затем воспользоваться симметрией гиперболы относительно оси Ох.

Замечание 2*. Можно уточнить расположение точек гиперболы (1) относительно ее асимптот у = ±  ^b/_a х.

Найдем расстояние от точки гиперболы, расположенной в первом квадранте координатной плоскости, до прямой у = ^b/_a х. Запишем ее уравнение в виде bx — ау = 0.

Задача определения расстояния от точки до прямой рассматривалась в § 36.

Пусть М (х₀; у₀) — точка гиперболы (х₀ > 0, у₀ > 0). Нормирующий множитель прямой bx — ау = 0, очевидно, равен

а нормированное уравнение имеет вид

Следовательно, для искомого расстояния MP (рис. 115), получаем выражение

Так как М (х₀; у₀) — точка гиперболы (1), то    b²х₀² — а²у₀² = а²b². Поэтому

Из полученной формулы следует, что если точка М (х₀; у₀) движется по гиперболе так, что ее абсцисса х₀ неограниченно возрастает, то расстояние ее до прямой у = ^b/_a х неограниченно убывает. В силу симметрии аналогичный вывод можно сделать и для других квадрантов плоскости.

Как мы уже видели (рис. 114), правая ветвь гиперболы расположена выше асимптоты у = — ^b/_a х и ниже асимптоты у = ^b/_a х.   Поэтому отношение ^b/_a полуосей гиперболы определяет ее форму. Чем меньше это отношение, тем сильнее сжата к оси Ох гипербола. Как и в случае эллипса, для характеристики формы гиперболы удобнее  пользоваться  не  отношением    ^b/_a    , а отношением  ^c/_a .

Отношение полуфокусного расстояния с к действительной полуоси а называется эксцентриситетом гиперболы. Эксцентриситет обозначается буквой ε. Таким образом,

ε = ^c/_a 

Так как для гиперболы с > а, то эксцентриситет гиперболы удовлетворяет неравенству ε  > 1.

Выразим эксцентриситет гиперболы через отношение ^b/_a ее полуосей:

           (4)

Формула (4) показывает, что меньшим значениям отношения ^b/_a соответствуют меньшие значения эксцентриситета. Следовательно, чем меньше эксцентриситет гиперболы, тем сильнее сжата она к оси абсцисс.

Замечание. Гипербола называется равносторонней (или равнобочной), если длины ее полуосей равны между собой. Поскольку для равносторонней гиперболы a = b, уравнение ее имеет вид

х² — у² = а².      (5)

Асимптотами равносторонней гиперболы являются прямые у = х и у = —х. Таким образом, асимптоты равносторонней гиперболы взаимно перпендикулярны.

Вычислим эксцентриситет равносторонней гиперболы. По формуле (4) находим

Равносторонняя гипербола изучалась в школе. Ее уравнение не имело вида (5), так как гипербола рассматривались в другой системе координат. Об этом будет рассказано в § 43.

Задача 1. Найти асимптоты гипербол

Построить гиперболы. Для каждой гиперболы найти эксцентриситет.

Для первой гиперболы а₁ = 5, b₁= 4. Уравнения  асимптот у = ⁴/₅ х и у = — ⁴/₅ x.
Для второй гиперболы а₂ = 5, b₂ = 2. Уравнения асимптот у = ²/₅ х и  у = — ²/₅ x.

Перед тем как нарисовать гиперболу, следует построить ее асимптоты и отметить вершины гиперболы. На рис. 116 изображены обе гиперболы.

Эксцентриситеты гипербол находим по формуле (4):

У второй гиперболы эксцентриситет меньше, следовательно, вторая гипербола расположена ближе (сильнее сжата) к оси Ох, чем первая.

Задача 2. Даны фокусы гиперболы F₁(—10; 0) и F₂(10; 0) и ее асимптота 4х + 3у = 0. Написать уравнение гиперболы.

Записав уравнение асимптоты в виде  у = — ⁴/₃х, находим отношение полуосей гиперболы ^b/_a = ⁴/₃ . Из условия задачи следует, что с =10. Поэтому а² + b² = 100 .

Задача свелась к решению системы уравнений

Подставляя   b = ⁴/₃а   во втоpое уравнение системы, получаем

откуда а² = 36 . Теперь находим    b² = ( ⁴/₃а  )² = ¹⁶/₉ • 36 = 64

Следовательно,   гипербола   имеет   уравнение

Задача 3. Написать уравнение гиперболы, вершины которой находятся в фокусах эллипса

а фокусы — в вершинах того же эллипса. Сделать чертеж.

Обозначим через а_г, b_г полуоси гиперболы, через с_г — ее полуфокусное расстояние.
Пусть а_э, b_э— полуоси эллипса, с_э —его полуфокусное расстояние.

Для того чтобы составить уравнение гиперболы, нужно найти а_г² и b_г² .
Из уравнения эллипса имеем а_э² = 25, b_э² = 16.
Из соотношения с_э² = а_э² — b_э² находим с_э² = 25—16 = 9.
По условию задачи а_г = с_э и с_г = а_э, следовательно, а_г² = с_э²  и  с_г² = а_э².
Поэтому а_г²  = 9 и с_г² = 25. Так как для гиперболы с_г² = а_г² + b_г²,
то b_г² = c_г² — а_г² = 25 — 9 = 16.
Следовательно, искомое уравнение гиперболы таково:

Чертеж дан на рис. 117