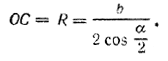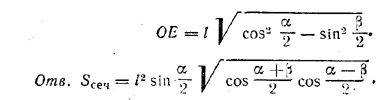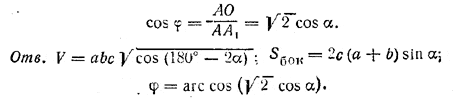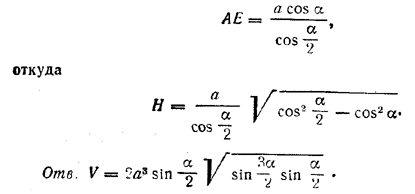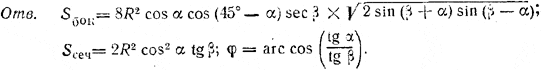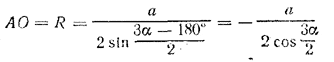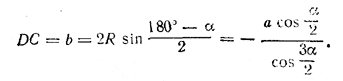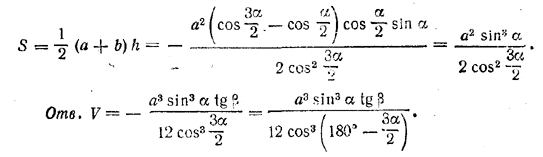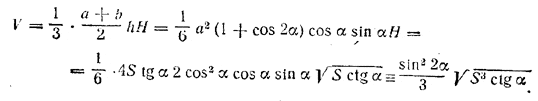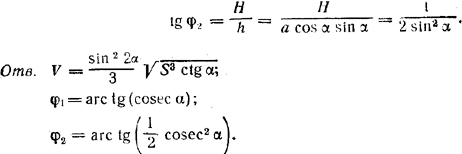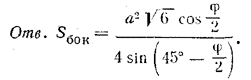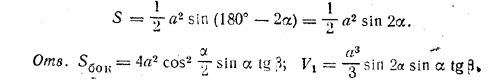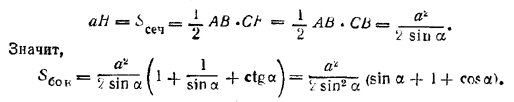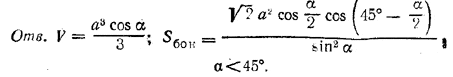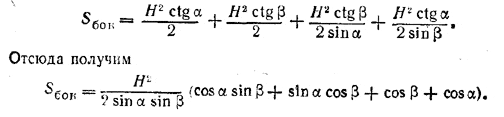ГЛАВА   2

МНОГОГРАННИКИ

Ответы и решения

 

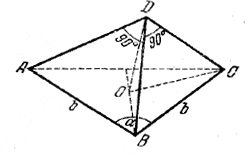
158.  Все боковые ребра пирамиды равны как стороны равнобедренных прямоугольных треугольников  (рис   145), поэтому высота DO пирамиды будет проходить через центр О окружности, описанной около основания;

Socн. = 1/2 b2 sin α

рис   145

Из  треугольника   DOC   Haxoдим

Н = √DC2— ОС2  ,

где DC = b/√2 , а  OC = R есть радиус окружности, описанной около треугольника  ABC.   Так   как   треугольник   ABC — равнобедренный, то /  BAC = 90° — α/2 и, следовательно, по теореме синусов

ВС = 2R sin (90° — α/2),

откуда

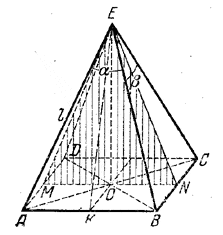
Отв. V = 1/6 b2  sin α/2 √cos α  

______________________________________________

159. Высота пройдет через центр окружности, описанной околооснования (рис. 146). См. предварительное  замечание  к  задаче  102 .

рис. 146

Биссектрисы углов AED и ВEС будут также медианами  равнобедренных  треугольников  AED   и  ВЕС.   

Площадь сечения MEN равна MN/2 • ОЕ, причем MN/2 = АК = l sin α/2. Из   треугольника ЕОК находим

ОЕ = √ЕК2 — ОK2 ,

где ЕК = l cos α/2 и ОK = BN = l  sin β/2, так что

______________________________________________

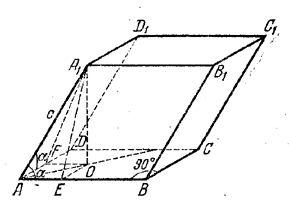
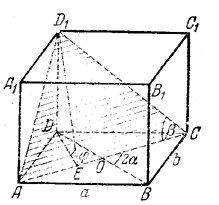
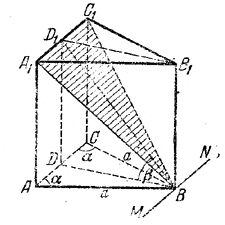
160.Проведем  через вершину  А1   (рис.   147)    плоскости A1ЕО перпендикулярно   к   АВ   и   A1FO    перпендикулярно   к   AD.    

рис.   147

Эти плoскости будут перпендикулярны к плоскости основания (доказать!) и линия их пересечения A1O  будет высотой параллелепипеда. Образовавшиеся прямоугольные треугольники А1АЕ и A1AF равны между собой (по общей гипотенузе АА1 = с и равным углам /  A1AE = /  A1AF = α). Следовательно, A1E = A1F и поэтому будут равны треугольники А1ОЕ и A1OF, а значит, OE = OF и прямая АО — биссектриса угла BAD.

Имеем H = √A1E2 — ОE2. Так как AEOF — квадрат, то ОЕ=АЕ. Находим AE и А1Е из треугольника AA1E; получаем    Н = с √sin2 α — cos2α = с √1 — cos 2α.

Замечание. В трехгранном угле при вершине А два плоских угла равны каждый α и третий угол прямой; следовательно, сумма двух плоских углов 2α должна быть больше третьего (90°), т. е. 2α > 90° или α > 45°. При этом условии — cos2α > 0 и, следовательно, Н имеет действительное значение. Боковое ребро AA1 образует с плоскостью основания /  A1AО = φ, так как АО — проекция ребра на основание

______________________________________________

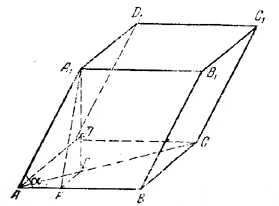
161. Построение  в  этой задаче то же, что в   предыдущей    

рис. 148

Биссектриса угла BAD будет диагональю ромба АС (рис. 148)

Из треугольника АА1Е находим

H = √AA12 — AE2

где  AA1 = а;  для определения АЕ  находим   сначала AF из  /\ AA1F а потом АЕ из прямоугольного /\ AEF. Получим

______________________________________________

162. Задача решается аналогично предыдущей. Можно использовать тот же рис. 148. сняв в нем обозначение угла α = /  А1АВ и введя обозначения /  BAD = α и /  A1AD = φ.

Отв.  V = 2а2b sin α/2  √ sin (φ — α/2) sin (φ + α/2)

______________________________________________

163. Основание ABCD - прямоугольник (рис. 149).

рис. 149

Для построения линейного угла двугранного угла D1ACD проводим через ребро DD1 плоскость, перпендикулярную к АС; в пересечении с гранями двугранного угла получим линейный   угол /  D1ED = φ

Имеем

Обозначим

AB = DC= a,

BC = AD = b (a > b),  DD1= H,  D1E = h,  DE = h1

В равнобедренном треугольнике АОВ сумма внутренних углов при основании АВ равна внешнему углу 2α, следовательно, /  ВАС = α. Из /\ ABC находим

a = 2R cos α;   b = 2R sin α.

Из /\ DEC, где /  ACD = α, находим

h1 = a sin α = 2R cos α sin α    и      ЕС = а cos α = 2R cos2 α.

Из /\ D1EC находим

h = EC•tg β = 2R cos2 α tg β.

Из /\ D1DE находим

H = √D1E2 — DE2   = √h2 — h12   = √4R2cos4 α tg2 β — 4R2 sin2α cos2 α =

= 2R cos2 α √tg2 β — tg2α

Выражение tg2 β — tg2α преобразуем, как в задаче 150.

______________________________________________

164.  Если катет AС (рис. 150) стягивает дугу, равную 2β , то /  AВС, как вписанный, опирающийся на эту дугу, будет равен β.

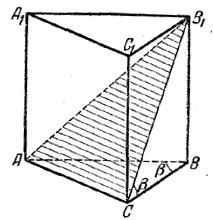
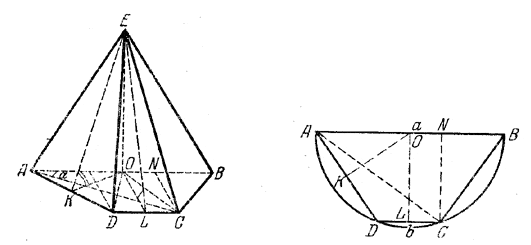
рис. 150

Плоскость, проходящая через диагональ В1С перпендикулярно к грани BB1C1C, должна пройти через AС, так как АС перпендикулярна к этой грани; линейный угол двугранного угла В1АСВ будет /  B1CB = β. Гипотенуза AВ есть диаметр описанной окружности и, следовательно, AB = 2R. Обозначим ВС = а, АС = b и АВ = с. Плоскость ACB1отсекает от призмы четырехугольную пирамиду  B1AA1C1C. Так как объем пирамиды В1АВС равен 1/3 объема призмы, то объем оставшейся четырехугольной пирамиды равен  2/3   объема  призмы.    Если    через    V1    обозначим объе.м пирамиды B1AA1C1C, а через V — объем призмы, то

V1 = 2/3V  = 2/3 • ab/2 • H = abH/3

Из /\ ABC   находим а и b, а    из  /\  B1BC   находим Н.   Для боковой поверхности получим следующее выражение

Sбок. = (2R cos β + 2R sin β + 2R)•2R cos β tg β = 4R2 sin • (cos β + sin β + 1).

Выражение в скобках можно  привести к  виду, удобному для логарифмирования:

cos β + sin β + 1 = (1 + cos β) + sin β = 2 cos2  β/2 + 2 sin  β/2 cos β/2
= 2 cos β/2 (cos β/2 + sin β/2 ) = 2 cos β/2  sin [(90° — β/2 ) + sin β/2]   =
= 2 cos β/2 • 2 sin 45° cos (45° — β/2 ) =  2√2   cos β/2 cos (45° — β/2).

Отв.  Sбок. = 8 √2  R2 sin β cosβ/2 cos(45° — β/2)

           V1 = 4/3 R3 sin β sin 2β.

______________________________________________

165.  Высота  ЕО   (рис. 151, а)   проходит через центр   О   окружности,   описанной   около   трапеции   ABCD. См. предварительное  замечание  к  задаче  102 .  

 

рис. 151

Дуги  AD, DC и СВ  - (рис. 151, б) равны (так как по условию стороны AD, DC и СВ равны), причем /   B =180° — α измеряется половиной дуги ADC.

Значит, дуги AD, DC и СВ содержат   по   180°— α;   следовательно, дуга АтВ содержит 360° — 3 (180° — α) =3α — 180°. Из треуголышка АОВ, где АВ = а, находим

( величина cos 3α/2  отрицательна, ибо α — тупой   угол,   так   что 135° < 3α/2 < 270° ).

Из треугольника ODC находим

Из треугольника ADF, где AD = b и  /  A = 180° — α, находим высоту трапеции

Из треугольника ВОЕ (см. рис. 151, а), где OB = R и /  OВЕ = β, находим H = R tg β .

 Площадь основания

______________________________________________

166. Высота ЕО проходит через центр О окружности, описанной около трапеции ABCD  (рис. 152). См. предварительное  замечание  к  задаче  102 .

рис. 152

Угол АСВ = 90°, кзк вписанный в эту окружность, должен опираться на диаметр. Иначе говоря, центр О лежит на стороне АВ. Трапеция ABCD, как вписанная в окружность,—равнобочная,   так    что /   DAB = /   СВА.

Введем обозначения АВ = а; DC = b,  /  AEB = φ = 2α. По условию 1/2 аH = S, a из равнобедренного треугольника AЕВ имеем   а = 2H tg φ/2 =2H tg α.

Из згих двух уравнений находим

Н =√S ctg α     и     а = 2 √S tg α.

Сторону b = DC найдем из треугольника ADC, вписанного в окружность с диаметром а. В этом треугольнике

/  DAC = /  DAB — /  СAВ =  /  CBA — /  СAВ

Но    так    как    треугольник    АСВ — прямоугольный, то   /  CBA = 90° — /  CAB. Следовательно,

/  DAC = 90° — 2 /  CAB = 90° —2α,

и мы имеем

b = a sin (90°— 2α) = a cos2α.

Наконец, находим

CN = h = AC sin α = a cos α sin α.

Теперь получаем

Грань АВE образует с плоскостью ABCD прямой угол. Для определения угла φ1 образуемого гранью ADE с плоскостью ABCD, опустим перпендикуляр из О на AD (он изображается прямой ОК., параллельной диагонали BD, так как последняя перпендикулярна к   AD;   диагональ   BD   на   чертеже   не   изображена; /   EKO = φ1),

В   треугольнике   АОК   угол   OAK   равен /  AВС = 90° — /  CAB  = 90° — α. Поэтому

ОК = АО • sin (90° — α) = a/2 cos α

и 

Для определения угла φ2, образуемого гранью DCE с плоскостью ABCD, проводим OL_|_ DC; /  ELO = φ2 Так как OL = NC= h, то

______________________________________________

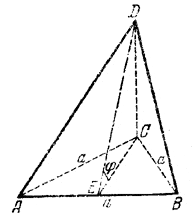
167. Нужно   определить   (рис.   153)   сумму   площадей   треугольников  ABC,   ABD  и  ACD.   

рис.   153

Площадь  S1   треугольника   ABC   равна

S1 = 1/2AB • CE  = 1/4 a2 √3

Площадь S2 треугольника ABD равна

площадь S3 треугольника ACD равна

S3 = 1/2 АС •  CD = 1/2АВ • CD = 1/2 АВ • СE • tg φ = S1 tg φ.

Следовательно,

Выражение в скобках преобразуется, как указано в задаче 164, и будет равно

2√2 cosφ/2 cos (45° —φ/2)  

Если в формуле для Sбок.  и  знаменателе  cos φ  представить  как sin (90° — φ),  то   выражение для Sбок.  можно будет сократить на

cos   (45° —φ/2).

______________________________________________

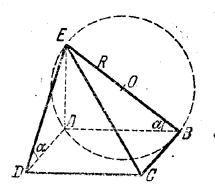
168. Так как плоскость основания ABC (рис. 154) проходит через прямую АС, а плоскость сечения А1ВС1 — через прямую A1C1, параллельную АС, то ребро MN двугранного угла β параллельно прямым АС и A1C1. 

рис. 154

Поэтому для построения линейного угла проводим BD_|_AC и BD1_|_A1C1 (точки D и D1 будут серединами АС и A1C1). Имеем

Sбок. = (2AB + АС) • DD1 = (2AB + АС) • BD • tgβ = 2a2(1 + cos S) sin α tg β.

Объем V1 четырехугольной пирамиды BACC1A1   равен  2/3  объема V призмы (см. задачу 164) и, следовательно,

V1 = 2/3 S• DD1

где

______________________________________________

169.  Как  в  задаче  121,  докажем,  что   грань  DCE   (рис.  155) наклонена   к   плоскости   основания   ABCD   под   углом   α =/  ADE, a грань  ВСЕ — под   равным   углом  α =/  АВЕ;   обе   эти   грани — прямоугольные треугольники ( / CDE = / CBE = 90°).

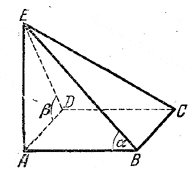
рис.  155

Площадь S1 треугольника ADE (а  также равная ей площадь треугольника   ABE)   равна S1 = 1/2 AB • AE. Из   треугольника   ABE, где BE = 2R, находим

AB = 2R cos α,         AE = 2R sin α,

так что S1 = 2R2 sin α cos α.

Площадь  S2 треугольника   CDE   (а   также  треугольника   СВE) равна

S2 = 1/2 BC • BE= 1/2 AB • BE = 2R2 cos α.

Имеем

Sп. = S+2S1+2S2 = 4R2(cos2α + cos α sin α + cos α) = 4R2cos α (cos α +sin α +1).

Выражение в скобках преобразуется, как указано в задаче 164.

Отв. Sп.= 8√2  R2 cos α cos α/2 cos (45° — α/2)

______________________________________________

170. Плоскость сечения ECD   (рис.  156), параллельного гипотенузе   АВ,   пересекает   плоскость   грани   АВВ1А1    по   прямой    ED, параллельной АВ.

рис.  156

Опустив перпендикуляры СМ и CF на прямые АВ и   ED,   получим   прямоугольный   треугольник  CMF,  где /  CFM = β   (доказать!) . Следовательно,

/\ CMF = /\ CMB

(у них общий  катет МС и /  СВМ = 90°— α, а по условию β = 90°— α).

Требуется  найти   объем   V  пирамиды   CABDE,  у   которой   основание ABDE — прямоугольник, а  высота равна СМ = a sin β = a cos α.

Имеем

V = 1/3• АВ • MF • СМ = 1/3• АВ • MB • CM = 1/3 • ВС2 • CM = 1/3 a3cos α

(катет   ВС   есть   средняя   пропорциональная    между   АВ   и   MB). Далее имеем

Sбок. = (ВС + AB + АС) Н = aH ( l + 1/sin α+ ctg α);

Здесь аН есть площадь грани СВВ1С1,   которая    по условию равна площади Scеч.  треугольника CDE. Следовательно,

Выражение в скобках преобразуется, как в задаче 164.

Чтобы    плоскость    CDE    пересекала    грань    ABB1A1, отрезок MF =MB = a sin α должен   быть   меньше,   чем   отрезок   

Из неравенства    находим sin 2 α <  1/2   т. е sin α < √2/2.     Значит, угол α должен    быть меньше 45°.

______________________________________________

171.   (рис. 157).

рис. 157

Боковая поверхность пирамиды будет

Выражение в скобках можно привести к виду,   удобному для логарифмирования, учитывая что

 

Получим

Заменив   через и преобразовав выражение в скобках как сумму синусов, получим

______________________________________________
Используются технологии uCoz