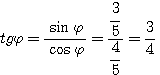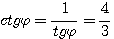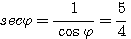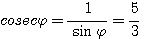Нахождение значений тригонометрических функций угла по значению какой-нибудь одной из них.

Используя основные тригонометрические тождества, легко найти значения всех тригонометрических функций sin х, cos х, tg x, ctg x, sec x, cosec x, если известно значение какой-нибудь одной из них. Поясним это на конкретных примерах.

Пример   1. Найти значения   тригонометрических функций  угла φ, если известно, что sin φ = ³/₅.

Из тождества sin² φ + cos²φ = 1  находим: cos²φ = 1 — sin² φ = ¹⁶/₂₅

Поэтому cos φ = ± ⁴/₅

Знак + или — следует выбирать в зависимости от того,  в какой четверти оканчивается угол φ.

По условию sin φ = ³/₅ > 0.

Значит, угол φ оканчивается либо в   1-й,  либо во 2-й четверти.
1)Если он оканчивается в 1-й четверти, то cos φ = + ⁴/₅.   
2)Если же он оканчивается во 2-й четверти, то cos φ = — ⁴/₅.

В  первом случае

Во втором случае

tg φ = — ³/₄;  ctg φ = —  ⁴/₃;  sес φ = —  ⁵/₄; cosec φ = ⁵/₃

Пример 2. Найти значения тригонометрических функций угла φ, если  известно,   что  он   оканчивается  в  4-й  четверти и  tg φ = — ³/₄

Используя тождество 1 + tg² φ = sec² φ, найдем sec φ:

sec φ = \/1 + tg² φ  = \/1+ (— ³/₄ ) ²  =  ⁵/₄

Знак + перед радикалом мы взяли потому, что угол φ по условию оканчивается в 4-й четверти, sec φ = ¹/_cosφ  , а косинус угла, оканчивающегося в 4-й четверти, положителен; поэтому положителен и sec φ.

Далее получаем:                 cos φ = ¹/_secφ = ⁴/₅

Теперь, используя тождество sin² φ + cos² φ = 1, найдем   sin φ:

sin φ = — \/ l — cos² φ = — ³/₅ .

Здесь перед радикалом нужно брать знак — ,  поскольку синус угла, оканчивающегося в 4-й четверти, отрицателен.

Заметим, что в данном случае рациональнее было бы   найти sin φ из тождества tg φ = ^{sin φ}/_{cos φ}  . Однако мы сознательно  получили  sin φ  другим путем, чтобы еще раз показать, как нужно  выбирать знак (+ или —) перед радикалом.

Итак, мы получили cos φ, sin φ, tg φ, sec φ. После этого легко найти значения и других тригонометрических функций угла φ:

ctg φ = ¹/_{tg φ} = — ⁴/₃  ;  cosec φ = ¹/_{sin φ} = — ⁵/₃

Упражнения

1.  Найти   значения   тригонометрических   функций   угла   α по  следующим данным;

1) sin α = 0,6  0°<α<90°;       4) cosα = —0,8, 180°<α<270°;

2) sinα= — ^\/2/₃, π <α< ³/₂  π; 5) tgα = —2,   ³/₂  π <α< 2π;

3) cosα= ¹²/₁₃, 270°<α<360°;       6) tgα =  ¹/₃ ,  180°<α<270°.

2.   Найти значения   тригонометрических   функций   угла  φ, если известно,  что
sin φ = ^\/2ab /_a+b     (a > b > 0)  и  угол φ оканчивается не в  1-й четверти.

3.   Найти   значения   тригонометрических   функций   угла   φ, если известно, что tg φ = а² — 1 ( |а| < 1), и угол φ оканчивается не во 2-й четверти.