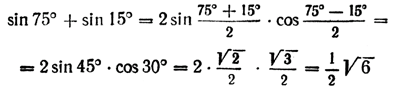Преобразование суммы (разности) синусов двух углов в произведение.

В предыдущем параграфе мы получили формулу

sin α • cos β =  ¹/₂ [sin (α + β)  +  sin (α — β)]             (1)

Эта формула верна для любых значений α и  β . Пусть α и  β таковы, что
α + β = х, α — β = у. Тогда α и  β найдутся как решение системы уравнений

Складывая эти уравнения почленно, получаем 2α = х + у. Вычитая эти уравнения почленно, получаем 2β = х —  у . Поэтому

Втаком случае тождество (1) можно переписать в виде:

откуда

 (2)

Сумма синусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразноста этих углов.

Заменяя в формуле (2) у на   — у   и учитывая, что sin ( — у) = — sin у,  получаем:

  (3)

Разность синусов двух углов равна удвоенному произведению синуса полуразности на косинус полусуммы этих углов.

Примеры.

1) Сумму sin 75° + sin 15°  легко вычислить без таблиц, если использовать формулу (2):

2) Разность sin ^5π/₁₂ — sin ^π/₁₂ легко   вычислить   без   таблиц, если использовать формулу (3):

Упражнения

1. Вычислить   без  таблиц,   используя  формулы для суммы и разности синусов двух углов:

а). sin 105° + sin 75°.

б). sin 105° — sin 75°.

в).sin ^11π/₁₂ +  sin ^5π/₁₂.

г).  sin ^11π/₁₂ —  sin ^5π/₁₂

д). cos ^π/₁₂ + sin ^7π/₁₂.

е). cos ^π/₁₂ — sin ^7π/₁₂.

2. Упростить данные выражения :

а).   sin (^π/₃ + α ) + sin ( ^π/₃ — α ).

б).   sin (^π/₃ + α ) — sin ( ^π/₃ — α ).

3.  Доказать тождества:

1 + sin α = 2cos² ( ^π/₄ — ^α/₂)

1 — sin α = 2sin² ( ^π/₄ — ^α/₂),

используя формулы для суммы и разности синусов двух углов.

4. Данные  выражения представить  в виде  произведений:

а).   ¹/₂ + sin α .              б).  \/3 — 2 sin α .

5. Доказать, что синусы углов α и  β равны тогда и только тогда, когда

α  =   (— 1)ⁿ β + nπ,

где n — некоторое целое число.