| 3ГОНОМЕТРИЯ В НАЧАЛО |
|
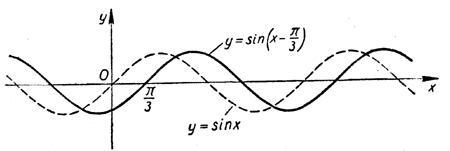
Графики тригонометрических функций у = A sin [ω ( x+ α ) ] Начнем с простого примера. Пусть нам требуется построить график функции у = sin (х + π/3). Для этого сравним данную функцию с функцией у = sin x, график которой мы уже умеем строить. Пусть данная функция у = sin (х + π/3) при х = х0 принимает некоторое значение, равное y0. Тогда y0 = sin ( х0 + π/3 ). Но в таком случае функция у = sin x должна принять то же самое значение y0 при х = х0 + π/3 . Таким образом, все значения, которые принимает функция у = sin (х + π/3) , принимает и функция у = sin х. Если х толковать как время, то можно сказать, что каждое значение y0 функцией у = sin (х + π/3) принимается на π/3 единицы времени раньше, чем функцией у = sin х. Отсюда вытекает, что график функции у = sin (х + π/3 ) получается посредством сдвига синусоиды у = sin x по оси абсцисс влево на π/3 .
Аналогично можно было бы построить и графики таких функций, как Заметим, что с подобными задачами мы уже сталкивались в части 1, при построении графика функции у = cos х = sin (х + π/2) . В программе Maple мы очень наглядно можем изобразить поведение функции у = sin (х + а ) , где а будет служить параметром анимации.Если при этом мы зададим пределы изменения а от 0 до 6,28 (2π) , то получим "плавно бегущую" влево синусоиду.
Если бы нам нужно было построить график функции у = sin (х — π/3), то рассуждения, аналогичные приведенным выше, дали бы такой результат. Функция у = sin (х — π/3) принимает те же значения, что и функция у = sin х, только с запаздыванием во времени (если аргумент х интерпретировать как время) на π/3. Поэтому график функции у = sin (х — π/3) получается посредством сдвига синусоиды у = sin х по оси абсцисс вправо на π/3.
Аналогично можно было бы построить и графики таких функций, как "Бегущая вправо" синусоида от Maple для функции у = sin (х — а) , где параметр анимации 0< a <6,28
Теперь рассмотрим более сложные примеры. Пусть нам нужно построить график функции у = A sin [ω ( x + α ) ]. Для этого сравним данную функцию с функцией Предположим, что функция у = A sin [ω ( x + α ) ] при х = х0 принимает некоторое значение, равное у0. Тогда у0 = A sin [ω ( х0 + α ) ] . Это соотношение показывает, что функция у = A sin ωх при х = х0 + α принимает то же самое значение у0. Поэтому все те значения, которые принимает функция Например, кривая у = 3 sin [ 2 (x + π/4 )] получается посредством сдвига кривой Кривая у = — 3 sin [ 2 (x + π/3 )] получается посредством сдвига кривой
Аналогично могут быть построены графики таких функций, как у = A sin [ω ( x— α ) ] у = A cos [ω ( x — α ) ] и т. д. Они получаются соответственно посредством сдвига графиков функций у = A sin ωх, у = A cos ωх и т. д. вправо по оси абсцисс на расстояние α. На рисунке вы видите график функции у = 3 sin [ 2 (x — π/4 )] , полуученный посредством сдвига графика функции у = 3 sin 2x вправо по оси абсцисс на расстояниеπ/4.
График функции у = 1/3 ctg [ 2 (x — π/3 )] , полученный посредством сдвига графика функции у = 1/3 ctg 2х вправо по оси абсцисс на расстояние π/3.
Заметим, что период функции у = A sin [ω ( x + α ) ], как и периоды других аналогичных тригонометрических функций, не зависит от α. Упражнения Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций: 1. а) у = sin (х + π/4 ); г) у = cos (x — π/6); б) у = sin (x — π/4); д) у = tg ( х + π/4 ); в) у = соs (x + π/6); е) у = tg (x — π/4). 2. у = 2 sin [ 3/2 (х + π/3 )]. 5. у = 1/2 sin [ 1/3 (х — π)]. 3. y = 1/2 сos [ 3/2 (х + π/4 )] 6. y = — 2 сos [ 2/3 (х — π)] 4. y = —1/2 tg [ 2 (х + π/3 )] 7. y = 2 tg [1/2 (х — π/4)] |
|
|