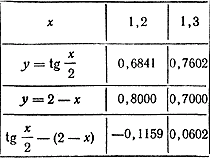| 3ГОНОМЕТРИЯ В НАЧАЛО |
|
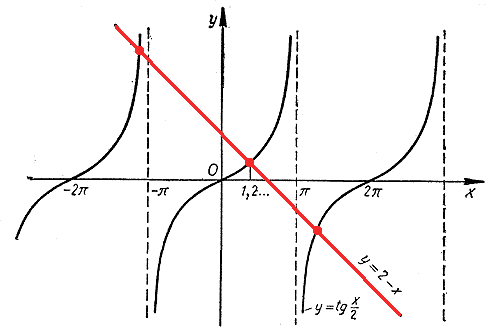
Графический способ решения тригонометрических уравнений О графическом способе решения некоторых тригонометрических уравнений мы уже говорили в части I. Теперь, умея строить графики тригонометрических функций кратных углов, мы можем решать этим способом гораздо больше уравнений, чем прежде. Но основная идея решения, конечно, остается той же самой. Для примера рассмотрим уравнение tg x/2 = 2 — x.
Графики функций у = tg x/2 и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х0. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2. Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе "Kалькулятор" или "Excel"). Выпишем значения функций у = tg x/2 и у = 2 — х в окрестности точки х = 1,2.
Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x/2 — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3(с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25 tg x/2 ≈ 0,7215, 2 — х = 0,7500. Поскольку tg x/2 < 2— х, то х0 >1,25. Итак, 1,25< х0 < 1,30. Теперь испытаем значение х = 1,28, которое близко к среднему значению чисел 1,25 и 1,30. При х = 1,28 tg x/2 ≈ 0,7445, 2 — х = 0,7200. Теперь уже tg x/2 >2 — х Значит , х0 < 1,28. Аналогично, рассматривая значение х = 1,26, мы получили бы tg x/2 < 2 — х и потому х0 > 1,26. Значит, 1,26 <х0< 1,28. Поэтому с точностью до 0,01 х0 ≈ 1,27 Если бы нужно было определить, какое это приближенное значение (с недостатком или с избытком), то нам пришлось бы сравнить значения tg x/2 и 2 — х в точке х = 1,27. Предлагаем учащимся сделать это самостоятельно. Упражнения 1. Найти наименьший положительный корень уравнения tg ( 2x — π/3 ) = 2— x2 с точностью до 0,01. 2. Найти корень уравнения sin 2х = 1 — 4х с точностью до 0,01. |
|
|