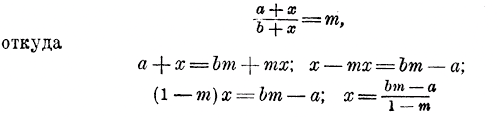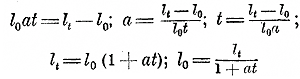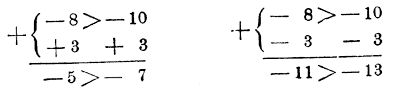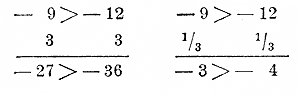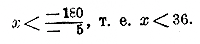| АЛГЕБРА В НАЧАЛО |
|
ОТДЕЛ ЧЕТВЕРТЫЙ. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ УРАВНЕНИЯХ. Глава первая. Пересмотр двух основных свойств уравнения. Пересмотр двух основных свойств уравнения. 120. Предварительное разъяснение. Всякое уравнение, как мы знаем, есть такое равенство, у которого обе части имеют одинаковую численную величину не при всяких значениях букв входящих в это равенство, а только при некоторых, которые в таком случае называются , к о р н я м и (или решениями) уравнения. Уравнение с одним неизвестным может иметь один корень, два корня и более; например, Два уравнения называются равносильными, если они имеют одинаковые корни(При одинаковой их кратности). Например, два уравнения х2 + 2 = 3х и 3х — 2 = х2 равносильны, так как у них одни и те же корни, именно 1 и 2, уравнения же 7x = 14 и х2 + 2 = 3х неравносильны, так как первое имеет только один корень 2, тогда как второе, кроме этого корня, имеет еще особый корень 1. Когда, решая какое-нибудь уравнение, мы совершаем над ним некоторые преобразования (перенесение членов, приведение подобных членов и пр.), то этими преобразованиями мы заменяем данное уравнение последовательно другими, более простыми, до тех пор, пока не получим уравнения самого простого вида: х = а; тогда мы говорим, что это число а и есть корень данного уравнения. Но утвержать это безошибочно мы можем только тогда, когда у нас есть уверенность, что все уравнения, полученные при преобразованиях, равносильны данному уравнению; когда мы, например, уверены, что не может быть такого случая, что данное уравнение имеет два корня, а мы нашими преобразованиями пришли к уравнению, имеющему только один корень. Все преобразования, которые нам приходилось совершать над уравнениями, основаны на двух свойствах уравнения, указанных нами в начале алгебры (отдел 1§ 39). Рассмотрим теперь эти свойства подробнее с целью определить, не может ли применение этих свойств нарушить когда-либо равносильность уравнений. 121. Первое из указанных свойств уравнений. Возьмем какое-нибудь уравнение, например такое: x2 + 2 = 3x, (1) Положим, что к обеим частям этого уравнения мы прибавили какое-нибудь одно и то же число m (положительное или отрицательное, или даже нуль); тогда мы получим новое уравнение: x2 + 2 + m = 3x + m (2) Разъясним, что это уравнение равносильно данному. Для этого достаточно убедиться, во-первых, в том, что всякий корень уравнения (1) удовлетворяет и уравнению (2); и, во-вторых, обратно, в том, что всякий корень уравнения (2) удовлетворяет и уравнению (1). а) Пусть уравнение (1) имеет какой-нибудь корень, напримeр х = 1. Это значит, что когда в это уравнение на место х подставим 1, то выражение x2 + 2 сделается равным выражению 3x (каждое из этих выражений обратится в число 3). Но тогда при х = 1 суммы x2 + 2 + m и 3x + m сделаются равными, так как если к равным числам (3 и 3) прибавим равные числа (m и m), то и получим равные числа (3 + m и 3 + m). Значит, корень х = 1 должен быть также и корнем уравнения (2). Если уравнение (1) имеет еще какой-нибудь корень, то о нем можно сказать то же самое, что сейчар мы говорили о корне х = 1, т. е. что он удовлетворяет и уравнению (2). Таким образом, каждый корень уравнения (1) принадлежит и уравнению (2). б) Допустим, что уравнение (2) имеет какой-нибудь корень (например х = 2). Это значит, что если в это уравнение наместо х подставим 2, то выражение x2 + 2 + m сделается равным выражению 3x + m (именно, каждое из этих выражений обратится в число 6 + m). Нo тогда при х = 2 и выражения x2 + 2 и 3x сделаются равными, так как, если от равных чисел (6 + m и 6 + m) отнимем равные числа (m и m), то и получим равные числа. Значит, х = 2 есть также корень и уравнения (1). Если бы уравнение (2) имело еще какой-нибудь корень, то о нем можно было бы повторить то же самое, что мы сейчас сказали о корне х = 2, т. е. что и этот другой корень должен удовлетворять и уравнению (1). Значит, всякий корень уравнения (2) должен быть и корнем уравнения (1). Если же корни уравнений (1) и (2) одни и те же, то уравнения эти равносильны. Свойство это относится и к вычитанию из частей уравнения одного и того же числа, так как вычитание какого-нибудь числа равносильно прибавлению другого числа с противоположным знаком. Таким образом, если к обеим частям уравнения прибавим, или от них вычтем, одно и то же число, то получим новое уравнение, равносильное первому. На этом свойстве, как мы видели (отдел1 § 41), основано перенесение членов уравнения из одной части в другую с переменою знака. Теперь мы убеждаемся, что такое перенесение никогда не может нарушить равносильности уравнений. 122. Второе свойство уравнений. Возьмем то же самое уравнение x2 + 2 = 3x, и умножим обе его части на какое-нибудь число m, положительное или отрицательное, но только не на нуль. Тогда получим новое уравнение: (x2 + 2 )m = 3xm, Чтобы обнаружить равносильность этих двух уравнений, будем рассуждать совершенно так же, как мы рассуждали относительно первого свойства, а именно, покажем, во-первых, что всякий корень уравнения (1) удовлетворяет уравнению (2) и, во-вторых, обратно, что всякий корень уравнения (2) удовлетворяет уравнению (1). а) Пусть уравнение (1) имеет какой-нибудь корень, например х = 1. Это значит, что когда в это уравнение на место х подставим 1, то выражение x2 + 2 сделается равным выражению 3x (каждое из этих выражений обратится в число 3). Но тогда при х = 1 и произведения (x2 + 2 )m и 3xm сделаются равными, так как если равные числа (3 и 3) умножим на одно и то же число (m ), то и получим равные числа (3m и3m). Значит, корень х = 1 должен быть также и корнем уравнения (2). Так как все это можно повторить о всяком ином корне уравнения (1), то заключаем, что всякий корень уравнения (1) принадлежит и уравнению (2). б) Обратно, пусть уравнение (2) имеет какой-нибудь корень (например х = 2). Это значит, что если в это уравнение на место х подставим 2, то произведения (x2 + 2 )m и 3xm сделаются равными (каждое из них обратится в число 6m). Но тогда при х = 2 и выражения x2 + 2 и 3x сделаются равными, так как если равные числа (6m и 6m) разделим на равные числа (m и m), то и получим равные числа (6 и 6). Значит, всякий корень уравнения (2) должен быть и корнем уравнения (1). Таким образом уравнения (1) и (2) имеют одни и те же корни, т. е. они равносильны. Если бы число m было нуль, то после умножения мы не получили бы равносильного уравнения. Например, уравнение x2 + 2 = 3x имеет 2 корня: 1 и 2, когда же умножим обе его части на 0, то получим новое уравнение: (x2 + 2)•0 = 3x •0, которое имеет бесчисленное множество произвольных корней, так как произведение всякого числа на нуль равно нулю. Если, например, положим, что x = 10, то найдем: (102 + 2)•0 = 3• 10 •0, т. е. 102 • 0 = 30 • 0 или 0 = 0; приняв х = 20, получим: (202+2) • 0 = 3 • 20 • 0, т. е. 402 • 0 = 60 • 0, или 0 = 0, и т.д. Значит, от умножения частей уравнения на 0 уравнение перестает существовать, обращаясь в очевидное тождество: 0 = 0. Деление обеих частей уравнения на число, отличное от нуля, также ведет к равносильному уравнению, так как деление есть то же умножение, только на обратное число. Что же касается деления на нуль, то такое деление невозможно (отдел 1 § 33). Таким образом, если обе части уравнения умножим, или разделим, на одно и то же число, отличное от нуля, то получим новое уравнение равносильное первому. 123. Умножение или деление частей уравнения на одно и то же алгебраическое выражение. Иногда случается, что мы умножаем (или делим) части уравнения на одно и то же алгебраическое выражение. В этом случае надо задаться вопросом, не может ли это выражение при некоторых значениях букв обратиться в нуль. Если случится, что такие значения букв существуют, то при этих значениях нельзя умножать (или делить) части уравнения на наше алгебраическое выражение. Если мы об этом исключении забудем, то можем иногда впасть в ошибку. Приведем резкий пример такой ошибки. Пусть нам дано равенство: а = b. Преобразуем это равенство таким образом: умножим обе его части на а, предполагая, что а (следовательно, и Ь) не равно 0. Тогда получим: a2 = ab. Вычтем из обеих частей этого равенства по b2 получим: a2 — b2 = ab — b2 что можно переписать так: (а + b)(а — b) = b(а — b). Разделив теперь обе части равенства на а — b, получим: а + b = b, т. е. 2b = b (так как а = b) и, следовательно (по разделении обеих частей на b), 2 = 1,. Этот нелепый вывод получился от того, что мы разделили обе части равенства на а — b, не обратив внимания на то, что эта разность при нашем задании (а = b) есть нуль, а на нуль делить невозможно. 124. Посторонние корни. Умножать обе части уравнения на одно и то же алгебраическое выражение приходится, между прочим, тогда, когда мы решаем уравнение, содержащее дроби, в знаменатели которых входит неизвестное. Пусть, например, надо решить уравнение:
Общий знаменатель всех дробей есть, очевидно, (х — 2)2. Приведя все члены к этому знаменателю:
отбросим его, т. е., другими словами умножим все члены на (х — 2)2: х 2 + 2 = х — 2 + 2х + 2 т. е. х 2 + 2 = 3х;. (2) Мы получили уравнение второй степени. Как решаются такие уравнения, мы увидим впоследствии; но полученное нами уравнение настолько просто, что мы легко можем сообразить, что оно имеет два корня: 1 и 2. Если это уравнение (2) равносильно данному уравнению (1), то тогда и уравнение (1) должно иметь те же корни 1 и 2. Но заранее ручаться за равносильноcть этих двух уравнений мы не можем, так как для перехода от уравнения (1) к уравнению (2) нам пришлось обе части первого уравнения умножить на алгебраическое выражение (х — 2)2, которое при х = 2 обращается в нуль, а при умножении на нуль равносильность уравнений может нарушиться. Значит, надо испытать значение х = 2. Подставив это значение в данное уравнение, находим, что оно принимает невозможный вид: 4/0 + 2/0 = 1/0 + 6/0 (деление на нуль невозможно). Таким образом, корень х = 2 является посторонним для данного уравнения. Мы видим таким образом, что если в данном уравнения имеются дроби, знаменатели которых содержат неизвестное, и мы освободились от этих знаменателей, умножив обе части уравнения на общий знаменатель, то, найдя корни полученного уравнения, мы должны еще подстановкой испытать их, с целью определить, нет ли среди корней посторонних. 3 а м е ч а и и е. При делении частей уравнения на алгебраическое выражение, содержащее неизвестное, мы можем иногда потерять корень, именно то значение неизвестного (одно или несколько), при котором это выражение обращается в нуль. Пусть, например, дано уравнение: х 2 — 1 = (5 — х)(х — 1). Разложив его левую часть на два множителя, мы можем уравнение представить так: (х — 1)(х + 1) = (5 — х)(х — 1). Легко сообразить, что это уравнение имеет два корня: х = 1 и х = 2. Если же разделим обе части уравнения на х—1, то получим новое уравнение: х + 1 = 5 — х, которое имеет только один корень х = 2. Значит, от деления на х — 1 мы потеряла корень х =1, именно тот, который обращает в нуль разность х — 1. Решения положительные, отрицательные, нулевые и другие. 125. Общий вид уравнения первой степени с одним неизвестным. Положим, что мы упростили уравнение о одним неизвестным, выполнив следующие преобразования: раскрыли скобки; освободились от знаменателей; перенесли неизвестные члены в левую часть уравнения, а известные — в правую и сделали приведение подобных членов. Если после этого в левой части окажется только член с неизвестным х в первой степени, то такое уравнение называется уравнением первой степени с одним неизвестным. Значит, общий вид такого уравнения есть следующий: ах = b, где а и b могут быть числами и положительными, и отрицательными, и равными нулю. Рассмотрим, какого рода решения получает это уравнение при различных численных значениях букв а и b. 126. Положительное решение. Такое решение получается тогда, когда числа а и b оба положительны или оба отрицательны. x = 6/3 = 2 или x = —6/—3 = 2 Положительное решение, удовлетворяя уравнению, вместе с тем удовлетворяет и той задаче, из условий которой это уравнение выведено, если только в уравнении выражены все условия данной задачи. Но иногда может случиться, что не все условия задачи выражены в уравнении; тогда положительное решение, удовлетворяя уравнению, может иногда и не удовлетворить задаче. Приведем этому пример. Задача. Рабочий кружок, состоящий из 20 человек взрослых и подростков, устроил сбор на покупку книг, для библиотеки, причем каждый взрослый внес по 3 руб., а каждый подросток по 1 руб. Сколько было в этом кружке взрослых и сколько подростков, если весь сбор составил 55 руб.? Обозначим число взрослых буквой х ; тогда число подростков будет 20— х, и сбор со взрослых окажется 3х руб., а с подростков 20 — х руб. Согласно условию задачи получим уравнение: 3х + (20 — х) = 55, откуда x = 17 1/2 Это положительное решение, конечно, удовлетворяет уравнению, но не удовлетворяет задаче, так как по смыслу ее искомое число должно быть целым. Различие между уравнением и задачею произошло здесь от того, что уравнение не содержит в себе подразумеваемого в задаче требования, чтобы искомое число было целым. Предложенная задача оказывается невозможной. 127. Отрицательное решение. Такое решение получается из уравнения ах = b тогда, когда числа а и b имеют противоположные знаки. Пусть, напр., 5х = — 15, или — 5х = 15; тогда х = —15/5= — 3 или х = 15/—5 = — 3 Отрицательное решение надо понимать в смысле противоположном тому, в каком понимается положительное решение; напр., если положительное решение означало бы прибыль, выигрыш, время в будущем и пр., то отрицательное решение должно означать убыток, проигрыш, время в прошедшем и т. п. Если же случится, что по смыслу задачи неизвестное число х нельзя понимать в двух противоположных смыслах, то тогда отрицательное решение означает просто невозможность задачи. Задача. Какое число надо приложить к числителю и знаменателю дроби 13/17, чтобы получить дробь, равную 3/4? Обозначив искомое число буквой х, получим уравнение:
Так как это уравнение представляет собой пропорцию, то (13 + х) • 4 = (17 + х) • 4; значит: 52 + 4x = 51 + 3х, откуда: 4x — 3x = 51 — 52 = — 1, т. е. х = — 1. Но приложить — 1 это все равно, что отнять 1. Значит, получившееся отрицательное решение дает ответ на такую задачу: какое число надо отнять от числителя и знаменателя дроби 13/17, чтобы получить дробь, равную 3/4 . B нашем примере надо отнять по 1. 128. Нулевое решение. Положим, что в уравнении ах = b число b окажется нулем, а коэффициент а будет какое-нибудь число, отличное от нуля. Пусть, напр., уравнение будет: 4x = 0. Значит, уравнение требует, чтобы произведение 4х равнялось нулю. Но произведение равняется нулю только тогда, когда какой-нибудь сомножитель равен нулю; следовательно, сомножитель х должен равняться нулю. И из формулы х = 0/4 видно, что х = 0. Нулевое решение, удовлетворяя уравнению, вообще удовлетворяет и задаче. Задача. Какое число надо приложить к числителю и знаменателю дроби 13/26, чтобы получить 1/2? Обозначив искомое число буквой х, мы получим уравнение
откуда 26 + 2x = 26 + x; x = 0. Это значит, что данная дробь сама равна 1/2 129. Случай, когда уравнение не имеет корня. Пусть в уравнении ах = b, число а окажется нулем, а число b не равно нулю; напр. 0 • х = 10. Такое равенство невозможно, так как какое бы число мы ни взяли для х, произведение 0 • х равно нулю, а не 10. Если бы мы, не заметив, что а = 0, разделили обе части уравнения на а, то получили бы для х такую формулу: x = b/a. Обнаружив затем, что а = 0, мы из этой формулы нашли бы: x = b/0. Так как такое равенство не имеет смысла (деление на нуль невозможно), то мы пришли бы к заключению, что уравнение при этих условиях не имеет корня, и, следовательно, задача, из условий которой составлено это уравнение, невозможна. 130. Как можно понимать равенство: x = b/0. Если в уравнении ах = b коэффициент а не равен нулю, а только близок к 0, то для х получается дробь: x = b/a. Зададимся вопросом, как изменяется величина этой дроби, если знаменатель ее все более и более приближается к нулю, а числитель остается неизменным. Предположим сначала, что числа а и b оба положительные. Возьмем для знаменателя а такие, напр., уменьшающиеся значения:
Тогда дробь — получит такие возрастающие выражения:
Отсюда видим, что при неограниченном уменьшении знаменателя а дробь- может превзойти любое данное число, как бы велико оно ни было (лишь бы только числитель b оставался без изменения). Вспомним, что это свойство дроби мы уже видели раньше (отдел 3 § 112), когда говорили о графике функции: y = 6/x, выражающей обратную пропорциональную зависимость. Там мы видели , что когда абсцисса х уменьшается, приближаясь к нулю (напр., переходя через значения: 1/2 ; 1/4 ; 1/8 ; 1/16 ; и т. д.), то ордината у, равная дроби 6/x, увеличивается неограниченно, так что кривая (гипербола), по мере приближения ее к оси у-ов, подымается вверх беспредельно. Если теперь допустим, что числитель а, или знаменатель b, или тот и другой — числа отрицательные, то сказанное сейчас может быть повторено и о такой дроби, но только надо тогда говорить не о величине самой дроби, а об абсолютной величине ее. Таким образом, если в дроби знаменатель неограниченно приближается к нулю, а числитель остается без изменения, то абсолютная величина дроби неограниченно увеличивается. Иногда для краткости речи условно говорят, что при а = 0 уравнение ах = b имеет бесконечное решение (бесконечный корень). Фразу эту нельзя понимать буквально, так как уравнение в этом случае совсем не имеет корня; фраза эта есть только краткое выражение следующего предложения: если в уравнении ах = b коэффициент а неограниченно приближается к нулю, а число b остается неизменным, то уравнение получает такое решение (положительное или отрицательное), которого абсолютная величина неограниченно возрастает. В том же смысле употребляется иногда краткая запись, вроде следующей:
(читается: m, деленное на нуль, равно плюс-минус бесконечности). Запись эта означает только то свойство дроби, что если знаменатель ее стремится к нулю, а числитель остается без изменения, то абсолютная величина дроби неограниченно увеличивается (или, как иногда говорят: стремится к бесконечности), причем сама дробь остается или положительной, или отрицательной (смотря по тому, имеет ли знаменатель, стремящийся к нулю, одинаковый знак с числителем или противоположный). Подобным же образом мы можем убедиться еще в следующем свойстве: если абсолютная величина знаменателя дроби неограниченно увеличивается, а числитель остается неизменным, то величина дроби неограниченно приближается к нулю. Свойство это сокращенно выражают таким условным равенством (которое тоже нельзя понимать буквально):
Это свойство дроби мы также видели на графике функции y = 6/x ; если абсцисса х этого графика возрастает беспредельно, то дробь уменьшается, неограниченно приближаясь к нулю, так что гипербола, по мере продолжения ее направо, все ближе и ближе придвигается к оси x - ов (никогда ее не достигая). 131. Неопределенное решение. Если в уравнении ах = b оба числа а и b окажутся нулями, то уравнение обращается в тождество: 0 • x = 0, верное при всяком значении х. Значит, в этом случае уравнение становится неопределенным, т. е. оно допускает бесчисленное множество произвольных решений. Если бы мы, не заметив, что а = 0, разделили обе части уравнения на а, то для х получили бы дробь b/a, которая при b = 0 и при а = 0 обращается в частное 0/0. Такое частное, по определению деления, может равняться любому числу (отдел 1 § 33); значит, и в этом случае мы убедились бы, что уравнение допускает бесчисленное множество решений. Задача. Какое число надо приложить к числителю и знаменателю дроби a/b чтобы эта дробь сделалась равной числу m? Обозначив искомое число буквой х, получим такое уравнение:
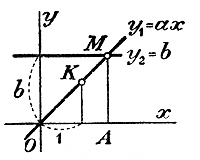
Допустим, что числа a, b и m заданы такими, что числитель и знаменатель дроби, выведенной нами для х, обратятся в нули, т. е., что bm = а и 1 = m. Тогда для х получается выражение 0/0 и, следовательно, уравнение и задача становятся неопределенными. И действительно, в этом случае а = b и дробь равна 1, какое бы число х мы ни прибавили к числителю и знаменателю. 132. Графическое истолкование решения уравнения ах = b. Из двух способов графического решения уравнения, указанных нами раньше (отдел 3 § 119), возьмем второй. Обозначим левую часть уравнения буквою у1 и правую часть буквою у2 и построим на одном и том же чертеже графики двух функций: у1 = ах и у2 = b. График первой функции есть прямая, проходящая через начало координат и через точку К (1, а), график второй функции есть прямая, параллельная оси x - ов и отсекающая от оси y-ов отрезок b
(на нашем чертеже мы изобразили случай, когда а >0 и b >0; предоставляем самим читателям сделать чертежи для случаев, когда: 1) а > 0, но b < 0; Пересечение этих двух прямых определит некоторую точку М, абсцисса которой ОА и будет корень уравнения ах = b, так как при этой абсциссе ордината прямой у1 = ах равна ординате прямой у2 = b, и, следовательно, ах = b. Пользуясь таким графическим изображением, мы можем наглядно истолковать все случаи решения уравнения ах = b. Ограничимся рассмотрением двух случаев: 1) „бесконечного" решения и 2) неопределенного решения.
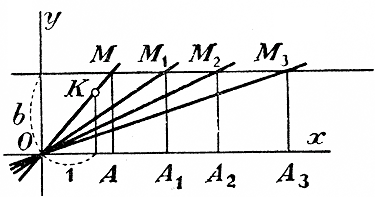
а) Бесконечное решение. Уменьшая численную величину коэффициента а, мы заставляем прямую у = ах все более и более приближаться к оси x - ов. Тогда точка М, в которой прямая у = b пересекается с прямой у = ах, все более и более удаляется направо, переходя через положения M1 M2, М3 и т. д., причем абсцисса ОА точки пересечения беспредельно увеличивается, переходя через значения OA1 ОА2, ОА3 и т. д. Значит, когда а неограниченно уменьшается, приближаясь к нулю, корень уравнения ах = b беспредельно возрастает. Таким образом:
(На чертеже мы брали случай, когда а > 0 и b > 0; в других случаях мы могли бы получить: х = b/0 = — ∞). б) Неопределенное решение получаетоя, как мы видели (§ 131), при а = b = 0. Чтобы истолковать этот случай графически, вообразим, что на нашем чертеже величина b уменьшается, приближаясь к нулю; тогда прямая у2 = b, оставаясь параллельною оси х-ов, будет все более и более приближаться к этой оси и при b = 0 сольется с нею. С другой стороны, прямая у1 = ах при а = 0 обратится тоже в ось x-ов, и тогда две прямые у2 = b и у1 = ах совпадут с осью x-ов, и, следовательно, каждую точку этой оси можно считать за точку пересечения; значит, величина корня остается неопределенной. 133. Буквенные уравнения. Нет надобности, чтобы неизвестное всегда обозначалось буквою х; оно может быть обозначено и какою угодно другою буквою. Возьмем, напр., формулу: s = 1/2 bh выражающую площадь s треугольника, у которого основание равно b линейных единиц и высота равна h таких же единиц. Формула эта представляет собой уравнение, в котором каждое из чисел s, b и h может быть принято за неизвестное. Пусть, напр., предложена такая задача: найти основание треугольника, у которого высота равна h каких-нибудь линейных единиц, а площадь составляет s соответствующих квадратных единиц. Тогда в нашей формуле число b должно считаться неизвестным, а числа s и h известными. Конечно, мы можем неизвестное основание обозначить буквою x и написать уравнение так: s = 1/2 hx откуда x = s : 1/2 h = 2s : h = 2s/h Но можно, не заменяя b на х, прямо из уравнения: s = 1/2 bh определить b в зависимости от s и h : s = 1/2 bh ; 2s = bh ; b = 2s/h Вообще надо привыкнуть решать не только численные уравнения, в которых данные числа выражены цифрами, а неизвестное обозначено буквой х , но и буквенные уравнения, в которых данные числа и неизвестное обозначены какими угодно буквами. Возьмем для примера еще формулу, известную из физики (см. задачу отдел 3 § 113): lt = l0 + l0 at в которой l0 означает длину какого-нибудь стержня при 0°, lt означает длину этого стержня при температуре t и а —так называемый коэффициент расширения вещества, из которого сделан стержень, т. е. число, показывающее, на какую долю длины при 0° увеличивается длина стержня при нагревании на каждый градус. В эту формулу входят 4 величины: l0 , lt , a и t; каждую из них можно принять за неизвестное, которое можно определить из формулы в зависимости от остальных трех величин. Так, из формулы находим:
Неравенства первой степени. 134. Определение понятий „больше" и „меньше". Когда мы говорим, что 10 больше 7, а 7 меньше 10, то мы разумеем при этом, что число 10 включает в себе как часть число 7, и что, следовательно, от 10 можно отделить (вычесть) 7, тогда как от 7 нельзя отделить 10; другими словами, мы хотим сказать, что разность 10—7 есть некоторое положительное число, тогда как разность 7—10 есть отрицательное число. Условимся распространить такое понимание о большем и меньшем и на числа относительные, а именно условимся, что относительное цисло а считается большим другою относительного числа b в том случае, когда разность a—b число положительное, и а считается меньшим b, когда разность а—b число отрицательное. При таком соглашении мы должны считать, что: а) Всякое положительное число больше всякого отрицательного; напр., + 3 > — 5, потому что разность (+3) — (— 5), равная сумме 3 + 5, есть число положительное. б) Всякое положительное число больше нуля по той же причине; напр., + 2 > 0 так как разность (+2) — 0 = + 2. * в) Всякое отрицательное число меньше нуля, так как разность между отрицательным числом и нулем всегда отрицательна; напр., — 3 < 0, так как (—3) — 0 = — 3. г) Из двух отрицательных чисел то больше, у которою абсолютная величина меньше; напр., —7 > — 9, так как разность (— 7) — (— 9) = (— 7) + 9 = + 2, т. е. она есть положительное число. Замечания. 1. Если желают кратко выразить, что число а положительное, то пишут: а > 0; если же желают показать, что число а отрицательное, то пишут: а<0. 2. Для ясного представления сравнительной величины относительных чисел всего лучше обратиться к наглядному изображению их на числовой прямой (отдел1 § 15). Выбрав произвольную единицу длины (аb), вообразим, что на неограниченной прямой вправо от какой-нибудь ее точки А, принятой за начало, отложены отрезки, изображающие положительные числа + 1, +2, +3... (и промежуточные), а влево от той же точки отложены отрезки, изображающие отрицательные числа — 1, —2, —3... (и промежуточные).
Тогда, двигаясь по этой прямой слева направо (по направлению стрелки), мы будем постоянно переходить от чисел меньших к большим, а двигаясь в обратном направлении, будем постоянно переходить от чисел больших к меньшим. 135. Свойства неравенств. Два числа или два алгебраических выражения, соединенные между собою знаками > или <, составляют неравенство. Как и равенство, неравенство состоит из двух частей: левой и правой. Так, если возьмем неравенство: 3 + 8 >10 — 2, то левая часть его будет 3 + 8, а правая 10 — 2. Обозначим левую часть неравенства одною буквою а, а правую часть другою буквою b. Тогда мы можем свойства неравенств высказать так: а) Если а > b, то b< а. Действительно, если а > b, то это значит, что разность а — b положительное число; но тогда разность b — a есть число отрицательное, и потому b < а. б) Если а > b и b > с, то а > с. Действительно, если а > b и b > с, то это значит, что обе разности: а — b и b — с положительные числа; но тогда и сумма этих разностей положительное число, а эта сумма равна: (а — b) + (b — с) = а — b + b — с = а — с Если же а — с > 0, то это значит, что a > с. в) Если а > b и m какое-нибудь относительное число, то а + m > b + m Действительно, если а > b, то это значит, что разность а — b положительное число; но тогда и разность (a + m) — (b + m) есть также положительное число, так как эта разность равна (а + m) — (b + m) = а + m —b — m = а — b. Пpимеpы.
Так как вычитание какого-нибудь числа равносильно прибавлению того же числа, но с противоположным знаком, то если а > b, то и а — m > b — m. Таким образом, если к обеим частям неравенства прибавим (или вычтем) одно и то же число, то знак неравенства не изменится (т. е. большее останется большим). г) Если а > b и m положительное число, то аm > bm. Действительно, если разность а — b положительное число, то и разность am — bm положительное число, так как эта разность равна (а — b) m, а произведение положительного числа на положительное есть положительное число. Пpимеpы.
Так как деление на какое-нибудь число равносильно yмнoжению на обратное число, то если а > b и m положительное число, то и a • 1/m> b • 1/m , т. е. а : m > b : т. Таким образом, если обе части неравенства умножим (или разделим) на одно и то же положительное число, то знак неравенства не изменится. д) Если а > b и m число отрицательное, то аm < bm. Действительно, если разность а — b положительное число, то разность am — bm будет отрицательное число, так как эта разность равна произведению положительного числа а — b на отрицательное число m. Примеры. Таким образом, если обе части неравенства умножим (или разделим) на одно и то же отрицательное число, то знак неравенства изменится на противоположный. 136. Решение неравенства 1-й степени с одним неизвестным. Задача. Найти число, четверть которого, увеличенная на 10, превосходит 2/3 числа, уменьшенного на 5. Обозначив искомое число буквою х, мы получим неравенство:
Неравенство это уподобляется уравнению 1-й степени с одним неизвестным. Решить неравенство, содержащее неизвестное, значит найти такое число или такие числа, которые, будучи подставлены в неравенства на место неизвестного, обращают его в очевидное тождественное неравенство. Решение неравенства первой степени выполняется так же, как и решение уравнения, так как две основные истины, на которых основано решение уравнений (§§ 121, 122), применимы и к неравенствам, с единственным исключением, что при умножении (или делении) обеих частей неравенства на одно и то же отрицательное число знак неравенства должен быть изменен на противоположный. Чтобы решить наше неравенство, освободим его сначала от знаменателей. Так как общий знаменатель 12, то умножим обе части неравенства на 12, от чего знак неравенства не изменится: 3x + 120 > 8x — 60. Теперь перенесем неизвестные в одну часть неравенства, а известные в другую (отняв от обеих частей неравенства по 120 и по 8х): 3x — 8х > — 60 — 120, т. е. — 5 х > — 180. Теперь разделим обе части на — 5, отчего знак неравенства изменится на противоположный:
(Можно было бы также сказать: обе части неравенства — 5x > —180 умножим на — 1, отчего знак неравенства изменится на противоположный: 5х < 180, и теперь разделим на 5.) Замечание. Более подробные сведения о неравенствах см. во 2-й части, § 404 и след. |