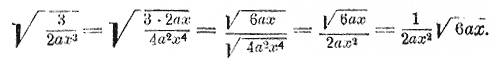| АЛГЕБРА В НАЧАЛО | ||
|
ОТДЕЛ ШЕСТОЙ. СТЕПЕНИ И КОРНИ. Глава первая. Возвышение в квадрат одночленных алгебраических выражений. Возвышение в квадрат одночленных алгебраических выражений. 152. Определение степени. Напомним, что произведение двух одинаковых чисел аа называется второю степенью (или квадратом) числа а, произведение трех одинаковых чисел ааа называется третьей степенью (или кубом) числа а; вообще произведение n одинаковых чисел аа... а называется n-ю степенью числа а. Действие, посредством которого находится степень данного числа, называется возвышением в степень (вторую, третью и т. д.). Повторяющийся сомножитель называется основанием степени, а число одинаковых сомножителей называется показателем степени. Сокращенно степени обозначаются так: а2, а3, а4... и т. д. Мы сначала будем говорить о простейшем случае возвышения в степень, именно о возвышении в квадрат; а пoсле рассмотрим возвышение и в другие степени. 153. Правило знаков при возвышении в квадрат. Из правила умножения относительных чисел следует, что: (+2)2=(+2) (+2) = + 4; (+1/3)2=(+1/3)(+1/3) = +1/9; (—2)2=(—2) (—2) = + 4; (—1/3)2=(—1/3)(—1/3) = +1/9 Вообще: (+a)2=(+a) (+a) = +a2 (—a)2=(—a) (—a) = +a2 Значит, квадрат всякого относительного числа есть число положительное. 154. Возвышение в квадрат произведения, степени и дроби. а) Пусть требуется возвысить в квадрат произведение нескольких сомножителей, напр. аbс. Это значит, что требуется аbс умножить на аbс. Но чтобы умножить на произведение аbс, можно умножить множимое на а, результат умножить на b и что получатся умножить еще на с . Значит: (аbс)2 = (аbс) (аbс) = (аbс) аbс = аbсаbс (мы отбросили последние скобки, так как от этого смысл выражения не изменяется). Теперь, пользуясь сочетательным свойством умножения (отдел1§ 34, б), сгруппируем сомножители так: (аа) (bb) (сс), что можно сокращенно написать: а2b2с2. Значит, чтобы возвысить произведение в квадрат, можно возвысить в квадрат каждый сомножитель отдельно Таким образом: ( 3/4 xy)2 = 9/16 x2 y2; (— 0,5mn)2 = + 0,25m2n2; и т. п. б) Пусть требуется какую-нибудь степень, напр. a3, возвысить в квадрат. Это можно выполнить так: (а3)2 = а3 • а3 = а3+3 = а6. Подобно этому: (х4)2 = x4 • x4 = x4+4 = x8 Значит, чтобы возвысить степень в квадрат, можно показатель степени умножить на 2. Таким образом, применяя эти два правила, будем, напр., иметь: (— 3 3/4 a x2 y3)2 = (— 3 3/4 )2 a2 (x2)2 (у3)2 = 225/2 a2 x4 y6 в) Пусть требуется возвысить в квадрат какую-нибудь дробь a/b. Тогда, применяя правило умножения дроби на дробь, получим:
Значит, чтобы возвысить в квадрат дробь, можно возвысить в квадрат отдельно числитель и знаменатель. Пример.
Возвышение в квадрат многочлена. 155. Вывод формулы. Пользуясь формулой (отдел2 глава3 § 61): (а + b)2 = a2 + 2аb + b2 , мы можем возвысить в квадрат трехчлен a + b + с, рассматривая его как двучлен (а + b) + с: (а + b +c)2 = [(а + b) + c ]2 = (а + b)2 + 2(а + b)c + c2 = a2 + 2аb + b2 + 2(а + b)c + c2 Таким образом, с прибавлением к двучлену а + b третьего члена с после возвышения в квадрат прибавились 2 члена: 1) удвоенное произведение суммы первых двух членов на третий член и 2) квадрат третьего члена. Приложим теперь к трехчлену а + b + с еще четвертый член d и возвысим четырехчлен а + b + с + d в квадрат, принимая сумму а + b + с за один член. (а + b +c + d)2 = [(а + b + c) + d ]2 = (а + b +c)2 + 2(а + b + c)d + d2 Подставив вместо (а + b +c)2 то выражение, которое мы получили выше, найдем: (а + b +c + d)2 = a2 + 2аb + b2 + 2(а + b)c + c2 + 2(а + b + c)d + d2 Мы опять замечаем, что с прибавлением нового члена к возвышаемому многочлену в квадрате его прибавляются 2 члена: 1) удвоенное произведение суммы прежних членов на новый член и 2) квадрат нового члена. Очевидно, что такое прибавление двух членов будет идти и дальше по мере прибавления новых членов к возвышаемому многочлену. Значит: Квадрат многочлена равен: квадрату 1-го члена, плюс удвоенное произведение 1-го члена на 2-й, плюс квадрат 2-го члена, плюс удвоенное произведение суммы первых двух членов на 3-й, плюс квадрат 3-го члена, плюс удвоенное произведение суммы первых трех членов на 4-й, плюс квадрат 4-го члена, и т. д. Конечно, члены многочлена могут быть и отрицательными. 156. Замечание о знаках. В окончательном результате со знаком плюс окажутся, во-первых, квадраты всех членов многочлена и, во-вторых, те удвоенные произведения, которые произошли от умножения членов с одинаковыми знаками. Пример.
157. Сокращенное возвышение в квадрат целых чисел. Пользуясь формулою квадрата многочлена, можно возвышать в квадрат всякое целое число иначе, чем обыкновенным умножением. Пусть, напр., требуется возвысить в квадрат 86. Разложим это число на разряды: 86 = 80 + 6 = 8 дес.+ 6 ед. Теперь по формуле квадрата суммы двух чисел можем написать: (8 дес.+ 6 ед.)2=(8 дес.)2 + 2(8 дес.) (6 ед.) + (6 ед.)2. Чтобы быстрее вычислить эту сумму, примем во внимание, что квадрат десятков составляет сотни (но могут быть и тысячи); напр. 8 дес. в квадрате образуют 64 сотни, так как 802 = б400; произведение десятков на единицы составляет десятки (но могут быть и сотни), напр. 3 дес. • 5 ед. = 15 дес, так как 30 • 5 = 150; и квадрат единиц составляет единицы (но могут быть и десятки), напр. 9 ед. в квадрате = 81 ед. Поэтому вычисление всего удобнее расположить так:
т. е. мы пишем сначала квадрат первой цифры (сотни); под этим числом пишем удвоенное произведение первой цифры на вторую (десятки), наблюдая при этом, чтобы последняя цифра этого произведения стояла на одно место правее последней цифры верхнего числа; далее, снова отступив последней цифрой на одно место вправо, ставим квадрат второй цифры (единицы); и все написанные числа складываем в одну сумму. Конечно, можно было бы дополнить эти числа надлежащим количеством нулей, т. е. написать так:
но это бесполезно, если только будем правильно подписывать числа друг под другом, отступая каждый раз (последней цифрой) на одно место вправо. Пусть еще требуется возвысить в квадрат 238. Так как: 238 = 2 сот. + 3 дес. + 8 ед., то
Но сотни в квадрате дают десятки тысяч (напр., 5 сот. в квадрате будет 25 дес. тысяч, так как 5002 = 250 000), произведение сотен на десятки дает тысячи (напр. 500 • 30= 15 000) и т. д. Значит:
Примеры.
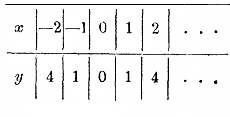
Графическое изображение функций: у = х2 и у = ах2. 158. График функции у = х2. Проследим, как при изменении возвышаемого числа х изменяется квадрат его х2 (напр., как при изменении стороны квадрата изменяется его площадь). Для этого предварительно обратим внимание на следующие особенности функции у = х2. а) При всяком значении х функция всегда возможна и всегда получает только одно определенное значение. Напр, при х = — 10 функция будет (—10)2 = 100, при б) Так как (—х)2 = х2, то при двух значениях х, отличающихся только знаками, получаются два одинаковые положительные значения у; напр, при х = — 2 и при х = + 2 значение у будет одно и то же, именно 4. Отрицательных значений для у никогда не получается. в) Если абсолютная величина х неограниченно увеличивается, то и у неограниченно увеличивается. Так, если для х будем давать ряд неограниченно возрастающих положительных значений: 1, 2, 3, 4... или ряд неограниченно убывающих отрица тельных значений: —1, —2, —3, —4..., то для у получим ряд неограниченно возрастающих значений: 1, 4, 9, 16, 25... Эти кратко выражают, говоря, что при x = + ∞ и при x = — ∞ функция у делается + ∞. г) Очень малому приращению переменного числа х соответствует и очень малое приращение функции у. Так, если значению х = 2, дадим приращение, положим, 0,1 (т. е. вместо х = 2 возьмем х = 2,1), то у вместо 22 = 4 сделается равным (2 + 0,1)2 = = 22 + 2 • 2 • 0,1 + 0,12. Значит, у увеличится на 2 • 2 • 0,1 + 0,12 = 0,41. Если тому же значению х дадим еще меньшее приращение, положим, 0,01, то у сделается равным (2 + 0,01)2 = = 22 + 2 • 2 • 0,01 + 0,012.. Значит, тогда у увеличится на 2 • 2 • 0,01 + 0,012= 0,0401, т. е. увеличится меньше, чем прежде. Вообще, чем на меньшую дробь мы увеличим х, тем на меньшее число увеличится у. Таким образом, если представим себе, что х увеличивается (положим от значения 2) непрерывно, переходя через все значения, большие 2, то у будет увеличиватьcя тоже непрерывно, переходя через все значения, большие 4. Заметив все эти свойства, составим таблицу значений функции у = х2, напр., такую:
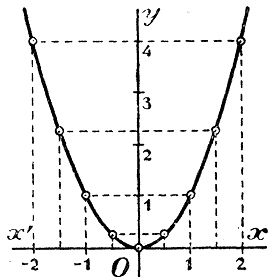
Изобразим теперь эти значения на чертеже в виде точек, абсциссы которых будут выписанные значения х, а ординаты соответствующие значения у (на чертеже за единицу длины мы приняли сантиметр); полученные точки обведем кривою. Кривая эта называется параболой.
Рассмотрим некоторые ее свойства. а) Парабола есть кривая непрерывная, так как при не прерывном изменении абсциссы х (как в положительном направлении, так и в отрицательном) ордината, как мы видели сейчас, изменяется тоже непрерывно. б) Вся кривая расположена по одну сторону от оси x-ов, именно по ту сторону, по какую лежат положительные значения ординат. в) Парабола подразделяется осью у-ов на две части (ветви). Точка О, в которой эти ветви сходятся, называется вершиною параболы. Эта точка есть единственная общая у параболы и оси x-ов; значит, в этой точке парабола касается оси x-ов. г) Обе ветви бесконечны, так как х и у могут увеличиваться беспредельно. Ветви поднимаются от оси x-ов неограниченно вверх, удаляясь в то же время неограниченно от оси y-ов вправо и влево. д) Ось y-ов служит для параболы осью симметрии, так что, перегнув чертеж по этой оси так, чтобы левая половина чертежа упала на правую, мы увидим, что обе ветви совместятся; напр, точка с абсциссой — 2 и с ординатой 4 совместитcя с точкой, имеющей абоциссу +2 и ту же ординату 4. е) При х = 0 ордината тоже равна 0. Значит, при х = 0 функция имеет наименьшее значение из всех возможных. Наибольшего значения функция не имеет, так как ординаты кривой увеличиваются беспредельно. 159. График функции вида у = ах2. Предположим сначала, что а есть число положительное. Возьмем, напр., такие 2 функции: 1) y = 1 1/2 x2; 2) y = 1/3 x2 Составим таблицы значений этих функции, напр., такие:
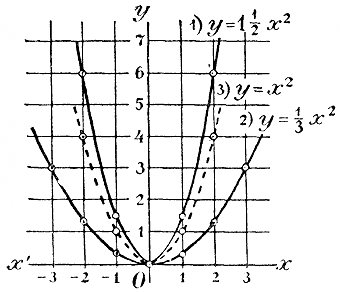
Нанесем все эти значения на чертеж и проведем кривые. Для сравнения мы поместили на том же чертеже (прерывистой линией) еще график функции: 3) y = x2
Из чертежа видно, что при одной и той же абсциссе ордината 1-й кривой в 1 1/2, раза больше, а ордината 2-й кривой в 3 раза меньше, чем ордината 3-й кривой. Вследствие этого все такие кривые имеют общий характер: бесконечные непрерывные ветви, ось симметрии и пр., только при а > 1 ветви кривой более приподняты вверх, а при a < 1 они более отогнуты книзу, чем у кривой y= x2 . Все такие кривые называются параболамми. Предположим теперь, что коэффициент а будет число отрицательное. Пусть, напр., y = — 1/3 x2. Сравнивая эту функцию с такой: y = + 1/3 x2 замечаем, что при одном и том же значении х обе функции имеют одну и ту же абсолютную величину, но противоположны по знаку. Поэтому на чертеже для функции y = — 1/3 x2 получится такая же парабола, как и для функции y = 1/3 x2 только расположенная под осью х-ов симметрично с параболой y = 1/3 x2. В этом случае все значения функции отрицательны, кроме одного, равного нулю при х = 0; это последнее значение является наибольшим из всех.
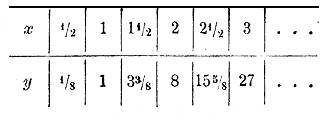
Замечание. Если зависимость между двумя переменными величинами у и х выражается равенством: у = ах2, где а какое-нибудь постоянное число, то можно сказать, что величина у пропорциональна квадрату величины х, так как с увеличением или уменьшением х в 2 раза, в 3 раза и т. д. величина у увеличивается или уменьшается в 4 раза, в 9 раз, в 16 раз и т. д. Напр, площадь круга равна π R2, где R есть радиус круга и π постоянное число (равное приблизительно 3,14); поэтому можно сказать, что площадь круга пропорциональна квадрату его радиуса.. Возвышение в куб и в другие степени одночленных алгебраических выражений. 160. Правило знаков при возвышении в степень. Из правила умножения относительных чисел следует, что (—5)3 = (—5)(—5)(—5) = —125; (—1/2)4= (—1/2) (— 1/2) (— 1/2) (— 1/2)=+1/16; (— 1)5 = (— 1) (— 1) (— l) (—1) (—1) = — l; (— 1)6 = (— 1) (— 1) (— l) (—1) (—1) (—1) = +l; и т. п. Значит, от возвышения отрицательного числа в степень с четным показателем получается положительное число, а от возвышения его в степень с нечетным показателем получается отрицательное число. 161. Возвышение в степень произведения, степени и дроби. При возвышении произведения степени и дроби в какую-нибудь степень мы можем поступать так же, как и при возвышении в квадрат ( § 154). Так: (аbс)3 = (аbс)(аbс)(аbс) = аbс • аbс • аbс = (ааа)(bbb)(ссс) = a3b3с3; Графическое изображение функций: у = х3 и у = ах3. 162. График функции у = х3. Рассмотрим, как при изменении возвышаемого числа изменяется куб его (напр., как при изменении ребра куба изменяется его объем). Для этого предварительно укажем следующие особенности функции у = х3 (напоминающие свойства функции у = х2, рассмотренные нами раньше, § 158): а) При всяком значении х функция у = х3 возможна и имеет единственное значение; так, (+ 5)3 = +125 и никакому другому числу куб числа + 5 равняться не может. Подобно этому ( — 0,1)3 = — 0,001 и никакому другому числу куб числа —0,1 равняться не может. б) При двух значениях х, отличающихся только знаками, функция х3 получает значения, также отличающиеся друг от друга только знаками; так, при х = 2 функция х3 равна 8, а при х = — 2 она равна —8. в) При возрастании х функция х3 возрастает и притом быстрее, чем х, и даже быстрее, чем х2 ; так при х = — 2, —1, 0, +1, + 2, +3, + 4... х3 будет = —8, — 1, 0, +1, + 8, +27, + 64... г) Очень малому приращению переменного числа х соответствует и очень малое приращение функции х3. Так, если значение х = 2 увеличим на дробь 0,01, т. е. если вместо х = 2 возьмем x = 2,01, то функция у будет не 23 (т. е. не 8), а 2,013, что составит 8,120601. Значит, функция эта увеличится тогда на 0,120601. Если значение х = 2 увеличим еще меньше, напр, на 0,001, то х3 сделается равным 2,0013, что составит 8,012006001, и, значит, у увеличится только на 0,012006001. Мы видим, таким образом, что если приращение переменного числа х будет все меньше и меньше, то и приращение х3 будет все меньше и меньше. Заметив это свойство функции у = х3, начертим ее график. Для этого предварительно составим таблицу значений этой функции, напр., такую:
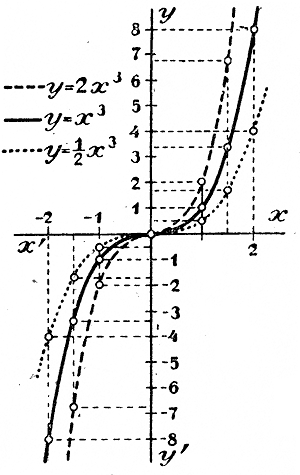
163. График функции у = aх3. Возьмем такие две функции: 1) у = 1/2 х3; 2) у = 2 х3 Если сравним эти функции с более простой: у = х3, то заметим, что при одном и том же значении х первая функция получает значения вдвое меньшие, а вторая вдвое большие, чем функция у = aх3, во вcем остальном эти три функции сходны между собой. Графики их изображены для сравнения на одном и том же чертеже. Кривые эти называются параболами 3-й степени. Основные свойства извлечения корня. 164. Задачи. а) Найти сторону квадрата, которого площадь равнялась бы площади прямоугольника с основанием 16 см и с высотою 4 см. Обозначив сторону искомого квадрата буквою х (см), получим такое уравнение: х2 =16 • 4, т. е. х2 = 64. Мы видим таким образом, что х есть такое число, которое, будучи возвышено во вторую степень, дает в результате 64. Такое число называется корнем второй степени из 64. Оно равно + 8 или — 8, так как (+ 8)2 = 64 и (— 8)2 = 64. Отрицательное число — 8 для нашей задачи не годится, так как сторона квадрата должна выразиться обыкновенным арифметическим числом. б) Свинцовый кусок, весящий 1 кг 375 г (1375 г), имеет форму куба. Как велико ребро этого куба, если известно, что 1 куб. см свинца весит 11 граммов? Пусть длина ребра куба будет х см. Тогда его объем будет равен х3 куб. см, а вес его окажется 11 х3 г. Значит: 11х3 = 1375; х3 = 1375 : 11 = 125. Мы видим таким образом, что х есть такое число, которое, будучи возвышено в третью степень, составляет 125. Такое число называется корнем третьей степени из 125. Оно, как нетрудно догадаться, равно 5, так как 53= 5 • 5 • 5 = 125. Значит, ребро куба, о котором говорится в задаче, имеет длину в 5 см. 165. Определение корня. Корнем второй степени (или квадратным) из числа а называется такое число, которого квадрат равняется а. Так, квадратный корень из 49 есть 7, а также и — 7, так как 72 = 49 и ( — 7)2 = 49. Корнем третьей степени (кубичным) из числа а называется такое число, которого куб равняется а. Так, кубичный корень из —125 есть — 5, так как ( — 5)3 =( —5)( —5)( —5)= —125. Вообще корнем n-ой степени из числа а называется такое число, которого n -ая степень равна а. Число n, означающее, какой степени находится корень, называется показателем корня. Корень обозначается знаком √ (знак радикала, т. е. знак корня). Латинское слово radix означает корень. Знак √ впервые введен в XV столетии.. Под горизонтальной чертой его пишут то число, из которого корень отыскивается (подкоренное число), а над отверстием угла ставят показатель корня. Так: корень кубичный из 27 обозначается.....3√27 ; корень четвертой степени из 32 обозначается ... 3√32. Показатель квадратного корня принято не писать вовсе, напр. вместо 2√16 пишут √16 . Действие, посредством которого отыскивается корень, называется извлечением корня; оно обратно возвышению в степень, так как посредством этого действия отыскивается то, что дано при возвышении в степень, именно основание стенени, а дано то, что при возвышении в степень отыскивается, именно сама степень. Поэтому правильность извлечения корня мы можем всегда поверять возвышением в степень. Напр., чтобы проверить равенство: 3√125 = 5, достаточно 5 возвысить в куб: получив подкоренное число 125, мы заключаем, что корень кубичный из 125 извлечен правильно. 166. Арифметический корень. Корень называется арифметическим, если он извлекается из положительного числа и сам представляет собою положительное число. Напр., арифметический квадратный корень из 49 есть 7, тогда как число — 7, которое тоже есть квадратный корень из 49, нельзя назвать арифметическим. Укажем следующие два свойства арифметического корня. а) Пусть требуется найти арифметический √49 . Такой корень будет 7, так как 72 = 49. Зададимся вопросом, нельзя ли подыскать какое-нибудь другое положительное число х, которое тоже было бы √49. Предположим, что такое число существует. Тогда оно должно быть либо меньше 7, либо больше 7. Если допустим, что x < 7, то тогда и х2< 49 (с уменьшением множимого и множителя произведение уменьшается); если же допустим, что x >7, то тогда и х2>49. Значит, никакое положительное число, ни меньшее 7, ни большее 7, не может равняться √49. Таким образом арифметический корень данной степени из данного числа может быть только один. К другому заключению мы пришли бы, если бы говорили не о положительном значении корня, а о каком-нибудь; так, √49 равен и числу 7, и числу — 7, так как и 72 = 49 и ( — 7)2 = 49. б) Возьмем какие-нибудь два неравные положительные числа, напр. 49 и 56. Из того, что 49 < 56, мы можем заключить, что и √49 < √56 (если только знаком √ будем обозначать арифметический квадратный корень). Действительно: 7 < 8. Подобно этому из того, что 64 < l25, мы можем заключить, что и 3√64 < 3√125 Действительно: 3√64 = 4 и 3√125 = 5 и 4 < 5. Вообще меньшему положительному числу соответствует и меньший арифметическии корень (той же степени). 167. Алгебраический корень. Корень называется алгебраическим, если не требуется, чтобы он извлекался из положительного числа и чтобы сам был положительный. Таким образом, если под выражением n√a разумеется алгебраический корень n -й степени, то это значит, что число а может быть и положительное и отрицательное, и самый корень может быть и положительным и отрицательным. Укажем следующие 4 свойства алгебраического корня. а) Корень нечетном степеци из положительного числа есть положительное число. Так, 3√8 должен быть числом положительным (он равен 2), так как отрицательное число, возвышенное в степень с нечетным показателем, дает отрицательное число. б) Корень нечетной степени из отрицательною числа есть отрицательное число. Так, 3√—8 должен быть отрицательным числом (он равен —2), так как положительное число, возвышенное в какую бы то ни было степень, дает положительное число, а не отрицательное. в) Корень четной степени из положительного числа имеет два значения с противоположными знаками и с одинаковой абсолютной величиной. Так, √+4 = + 2 и √+4 = — 2, потому что (+ 2)2 = + 4 и (— 2)2 = + 4; точно так же 4√+81 = + 3 и 4√+81 = — 3, потомуу что обе степени (+3)4 и (—3)4 равны одному и тому же числу. Двойное значение корня обозначается обыкновенно постановкою двух знаков перед абсолютной величиной корня; так пишут: √4 = ± 2; √a 2 = ± a; г) Корень четной степени из отрицательного числа не может равняться никакому ни положительному, ни отрицательному числу, так как и то и другое после возвышения в степень с четным показателем дает положительное число, а не отрицательное. Напр., √—9 не равен ни +3, ни —3 и никакому иному числу. Корень четной степени из отрицательного числа принято называть мнимым числом; относительные же числа называются вещественными, или действительными, числами. 168. Извлечение корня из произведения, из степени и из дроби. а) Пусть надо извлечь квадратный корень из произведения аbс. Если бы требовалось произведение возвысить в квадрат, то, как мы видели (§ 154), можно возвысить в квадрат каждый сомножитель отдельно. Так как извлечение корня есть действие, обратное возвышению в степень, то надо ожидать, что и для извлечения корня из произведения можно извлечь его из каждого сомножителя отдельно, т. е. что √abc = √a • √b • √c . Чтобы убедиться в верности этого равенства, возвысим правую часть его в квадрат (по теореме: чтобы возвысить в степень произведение...): (√a √b √c )2 = (√a )2(√b )2(√c )2 Но, согласно определению корня, (√a )2 = a, (√b )2 = b, (√c )2 = c Следовательно (√a √b √c )2 = аbс. Если же квадрат произведения √a √b √c равен аbс, то это значит, что произведение это равно квадратному корню из abc. Подобно этому: 3√abc = 3√a 3√b 3√c , так как (3√a 3√b 3√c )3 = (3√a )3 (3√b )3 (3√c )3 = abc Значит, чтобы извлечь корень из произведения, достаточно извлечь его из каждого сомножители отдельно. б) Легко убедиться поверкою, что следующие равенства верны: √a 4 = а2, потому что (a2)2 = а4; 3√x12 = x4, ,, „ (x4)3 = x12; и т. п. Значит, чтобы извлечь корень из степени, показатель которой делится на показатель корня, можно разделить показатель степени на показатель корня. в) Верны будут также и следующие равенства:
Значит, чтобы извлечь корень из дроби, можно изелень сю из числителя и знаменателя отоельно. Заметим, что в этих истинах предполагается, что речь идет о корнях арифметических. Примеры. 1) √9a 4b6 = √9 √a 4 √b 6= 3а2b3; 2) 3√125 a6 x9 = 3√125 3√a6 3√x9 = 5а2x3 Замечание Если искомый корень четной степени и предполагается алгебраический, то перед найденным результатом надо поставить двойной знак ± Так, √9x 4 = ± 3x2. 169. Простейшие преобразования радикалов, а) Вынесение множителей за знак радикала. Если подкоренное выражение разлагается на такие множители, что из некоторых из них можно извлечь корень, то такие множители, по извлечении из них корня, могут быть написаны перед знаком радикала (могут быть вынесены за знак радикала). Примеры. 1) √a 3 = √a 2a = √a 2 √a = а√a . 2) √24 a4 x3 = √4 • 6 a4 x2x = 2a2x √6x 3) 3√16 x4 = 3√8 • 2 x3x = 2x 3√2 x б) Подведение множителей под знак радикала. Иногда бывает полезно, наоборот, подвести под знак радикала множители, стоящие перед ним; для этого достаточно возвысить такие множители в степень, показатель которой равен показателю радикала, а затем написать множителями под знаком радикала. Примеры. 1) а2 √a = √ (а2)2 a = √ а4 a = √a5. 2) 2x 3√x = 3√(2x)3 x = 3√8x3 x = 3√8x4. в) Освобождение подкоренного выражения от знаменателей. Покажем это на следующих примерах: 1)
2)
Замечание. Если требуется извлечь корень из алгебраической суммы, то было бы ошибочно извлечь его из каждого слагаемого отдельно. Напр.√9 + 16 = √25 = 5, тогда как ____________ |
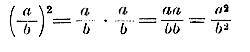
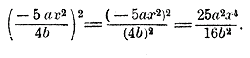
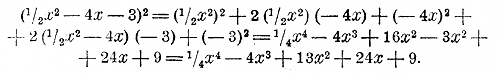
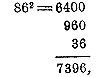
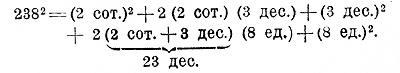
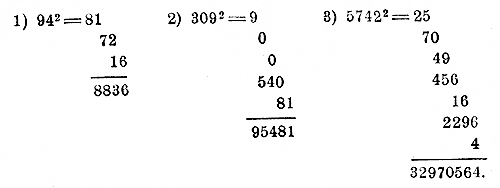
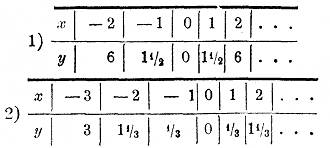
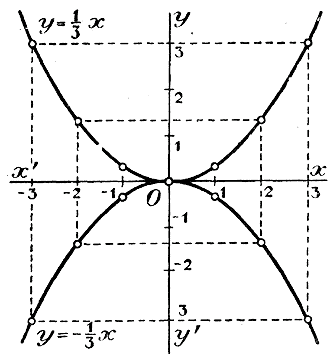
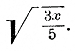Преобразуем дробь так, чтобы из знаменателя можно было извлечь квадратный корень. Для этого умножим оба члена дроби на 5:
Умножим оба члена дроби на 2, на а и на х, т. е. на 2ах: