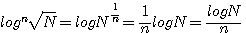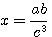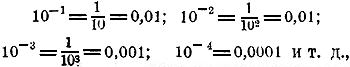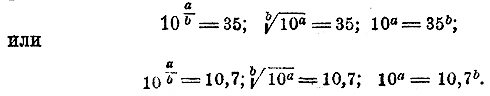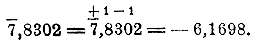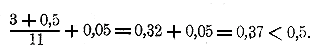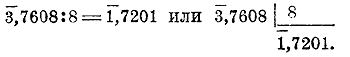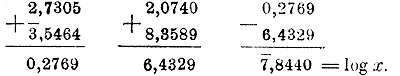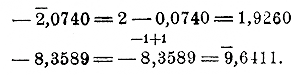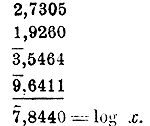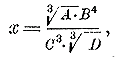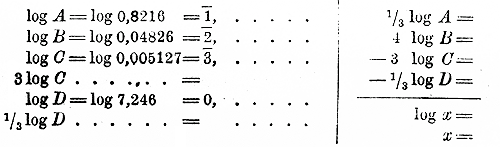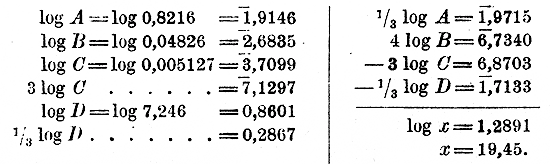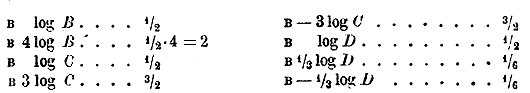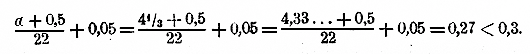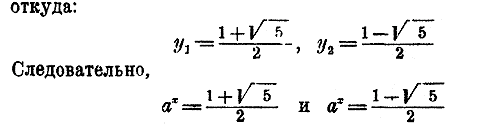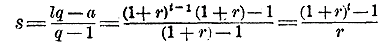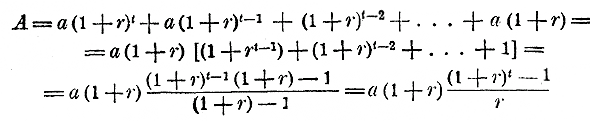| АЛГЕБРА В НАЧАЛО | ||||||||||||||||||||||||||||||||||||
|
ОТДЕЛ ДВЕНАДЦАТЫЙ ЛОГАРИФМЫ. |
||||||||||||||||||||||||||||||||||||
|
Глава первая. Общие свойства логарифмов. Глава первая. |
||||||||||||||||||||||||||||||||||||
|
Общие свойства логарифмов.
|
||||||||||||||||||||||||||||||||||||
|
267.Два действия, обратные возведению в степень. |
||||||||||||||||||||||||||||||||||||
|
Возьмем такие равенства: |
||||||||||||||||||||||||||||||||||||
|
23 = 2 . 2 . 2 = 8 |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Эти три примера выражают собой различные случаи действия, называемого возвышением в степень. Таких действий можно указать следующие два: 1) Пусть требуется узнать, какое число надо возвести в степень с показателем 3, чтобы получить число 12. Обозначив искомое число буквой х, мы можем написать уравнение: | ||||||||||||||||||||||||||||||||||||
|
х3=12 |
||||||||||||||||||||||||||||||||||||
| Действие, посредством которого находится основание х по данной степени и данному показателю ее, называется извлечением корня; оно обозначается, как мы знаем, так: | ||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
2) Положим, надо узнать, какой показатель должен быть у степени, в которую надо возвести основание 4, чтобы получить 16.Обозначив искомый показатель буквой х, можем написать уравнение: |
||||||||||||||||||||||||||||||||||||
|
4х = 16 |
||||||||||||||||||||||||||||||||||||
|
Действие, посредством которого находится показатель степени по данной степени и данному основанию, называется нахождением логарифма данного числа (16) по данному основанию (4). В нашем примере х = 2, так как 42 = 16. |
||||||||||||||||||||||||||||||||||||
|
Итак, возведение в степень имеет два обратных действия. Поставим вопрос, различны ли эти действия? Однако действия эти рассматриваются не как различные, а как одно и то же действие, называемое делением. Причина слияния этих двух обратных действий в одно заключается в переместительном свойстве умножения, по которохму произведение не меняется от перемены мест 1-го и 2-го сомножителя . В таком же положении находится и сложение (2 слагаемых); этому действию также можно указать два обратных действия — нахождение неизвестного числа (1-го слагаемого), к которому надо прибавить данное число (2-е слагаемое), чтобы получить данную сумму; другое — нахождение неизвестного числа (2-го слагаемого), которое надо прибавить к данному числу (к 1-му слагаемому), чтобы получить данную сумму. Однако эти два действия рассматриваются как одно, называемое вычитанием, вследствие того, что сложение обладает переместительным свойством, по которому сумма не зависит от порядка слагаемых. Если бы это свойство принадлежало также и возведению в степень, то тогда и два указанных выше обратных действия составляли бы в сущности одно. Но возведение в степень не обладает свойством переместительности; напр., 23 не равно 32, 102 не равно 210 и т. д. Вследствие этого нахождение основания по данным показателю и степени (извлечение корня) существенно отличается от нахождения показателя по данным основанию и степени (нахождение логарифма). Заметим, что последнее действие в элементарной алгебре подробно не рассматривается; указываются главным образом его практические применения. |
||||||||||||||||||||||||||||||||||||
|
268. Определение логарифма.
|
||||||||||||||||||||||||||||||||||||
|
Если, напр., основание будет 4, то |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
Если возьмем за основание 10, то |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
Вместо того, чтобы писать: „логарифм числа 16 по основанию 4" пишут сокращенно так: | ||||||||||||||||||||||||||||||||||||
|
log4 16, |
||||||||||||||||||||||||||||||||||||
|
помещая внизу знака log то число, которое служит основанием. Впрочем, если заранее известно, какое число принято за основание, то его не пишут. Вместо знака log ( сокращения слова "logarithme") иногда пишут lg или Log. |
||||||||||||||||||||||||||||||||||||
|
Прежде чем говорить о применениях логарифмов, мы предварительно рассмотрим свойства так называемой логарифмической функции. |
||||||||||||||||||||||||||||||||||||
|
269.Логарифмическая функция и ее график. Если в равенстве у = аx мы рассматриваем показатель х как независимое переменное , то тогда у будет функция от х, которую мы назвали раньше показательной. Но если в этом равенстве за независимое переменное мы будем считать у, то тогда х будет некоторая функция от у, а именно х есть логарифм числа у по основанию а, что можно выразить так: |
||||||||||||||||||||||||||||||||||||
|
x = loga y |
||||||||||||||||||||||||||||||||||||
|
Обозначая по принятому независимое переменное буквой х, а функцию от этого переменного буквой у (т. е. заменяя х на у и наоборот), мы ту же самую функцию можем записать так: |
||||||||||||||||||||||||||||||||||||
|
y = loga x |
||||||||||||||||||||||||||||||||||||
|
Такая функция называется логарифмической. Вспоминая то, что мы раньше говорили об обратной функции (Отдел 7 глава 3 §180), мы видим, что логарифмическая функция обратна показательной. |
||||||||||||||||||||||||||||||||||||
|
Построим графики следующих трех логарифмических функций: |
||||||||||||||||||||||||||||||||||||
|
1) y = log2х; 2) y = log ½ x; 3) y = log10x. |
||||||||||||||||||||||||||||||||||||
|
Для этого составим таблицы значений этих функций. Всего проще их можно сделать из таблиц соответственных показательных функций |
||||||||||||||||||||||||||||||||||||
|
1)у = 2х; 2) у = (1/2)х; 3) у = 10х, |
||||||||||||||||||||||||||||||||||||
|
поменяв в этих таблицах значения абсциссы х на значения ординаты у и наoборот. Сделав это, мы получим такие 3 таблицы: |
||||||||||||||||||||||||||||||||||||
|
1) y = log2х |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
2) y = log1/2x |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
3) y = log10x |
||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||
|
Нанеся все эти значения на чертеж и обведя все точки непрерывными кривыми, получим три графика взятых функций. Согласно свойству обратных функций , кривые эти — те же самые, которыми выражаются функции у = 2х; у = (1/2)х; у = 10х, только они расположены симметрично с этими кривыми относительно биссектрисы угла хОу. |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Имея график логарифмической функции, мы можем при помощи его найти логарифм (приближенный) числа, помещающегося между взятыми для чертежа значениями x. Возьмем, напр., график функции у = log2x и найдем при его помощи log2 6.
|
||||||||||||||||||||||||||||||||||||
|
270. Свойства логарифмической функции. 1) Так как графики всецело расположены направо от оси у -ов, то отрицательные числа не имеют логарифмов (вспомним, что при всяком значении х функция ах положительн 2) Всякой положительной абсциссе соответствует своя определенная ордината; значит, всякое положительное число имеет логарифм. 3) Все кривые пересекаются с осью х-ов в одной и той же точке, отстоящей от начала координат на + l. Это значит, что при всяком основании логарифм единицы есть нуль (а0 =1). 4) Когда a >1, то части кривых, соответствующие абсциссам, меньшим 1, лежат в угле x0y', а части кривых, соответствующие абсциссам, большим. 1, расположены в угле х0у. Это значит, что при основании, большем 1, логарифмы чисел, меньших 1, отрицательны, а логарифмы чисел, больших 1, положительны. Это вполне соответствует тому свойству показательной функции, что при положительном
значении х функция ах больше 1, а при отрицательном - меньше 1 (если а > 1). 5) Логарифм самого основания равен 1; так, на графике у = log2 x видно, что абсциссе 2 соответствует ордината 1; на других графиках видно то же самое. 6) При основании, большем 1, ветви кривых, расположенные ниже оси x-ов, при уменьшении абсциссы от 1 до 0, приближаются к полуоси 0у' как угодно близко, никогда, однако, ее не достигая, а ветви тех же кривых, расположенные выше оси x-ов, при возрастании х от 1 до
|
||||||||||||||||||||||||||||||||||||
|
271. Понятие о значении логарифмических таблиц. Различные числа можно выражать как степени одного и того же числа, напр., как степени числа 10. Такие числа, как 10; 100; 1000... или 0,1; 0,01; 0,001 и т. п., выражаются, как степени 10 очень просто: 10 = 101 ; 100 = 102; 1000 = 103;... 0,1 = 10-1, 0,01 = 10-2 0,001 = 10-3 и т. п. Другие числа выразить степенью 10 затруднительно.
Так, если требуется найти показатель степени, в которую нужно возвести
10, чтобы получить число 5, то мы можем только сказать, что искомый показатель больше 0, но меньше 1, так как 100 =1, что меньше 5, а 101 = 10, что больше 5; значит, показатель степени, в которую надо возвысить 10 для получения 5, должен быть некоторая положительная дробь меньшая 1. Мы можем даже сказать, что эта дробь больше 1/2 , но
меньше 3/4, так как Но найти точно показатель х, чтобы 10x = 5, очень затруднительно. Есть отделы математики, в которых указываются способы, как можно для всякогo данного числа N найти такой показатель х, при котором степень 10x или в точности равняется N, или отличается от этого числа как угодно мало. Ученые, пользуясь этими способами, составили так называемые логарифмические таблицы, в которых помещены различные числа
и около каждого из этих чисел указан показатель степени (логарифм), в которую надо возвести 10, чтобы получить это число. Разъясним, для какой цели могут служить такие таблицы. |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Извлекать корень 5-й степени мы не умеем. В подобных случаях нам могут помочь логарифмические таблицы. Находим в этих таблицах число 40 и около него логарифм этого числа. Пусть это будет 1,6... Это значит, что |
||||||||||||||||||||||||||||||||||||
|
40 = 101,6... |
||||||||||||||||||||||||||||||||||||
|
и следовательно, |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Так как при извлечении корня из степени показатель подкоренного числа (какой бы он ни был) делится на показатель корня, то |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Теперь в тех же таблицах в столбце логарифмов находим 0,32 и около него соответствующее число, пусть это будет, положим, 2,09... Это и будет приближенное значение |
||||||||||||||||||||||||||||||||||||
|
Мы вскоре увидим, что логарифмические таблицы во многих случаях позволяют производить такие действия над числами, которые без таблиц мы или совсем не могли бы выполнить (как в примере, только что указанном), или на выполнение которых потребовалось бы очень много времени. Теперь нам предстоит ознакомиться, во-первых, с тем, как при совершении какого-либо действия над данными числами можно найти логарифм искомого числа при помощи логарифмов этих данных чисел (взятых из таблиц) и, во-вторых, как найдя такой логарифм, отыскать по нему в таблицах искомое число. |
||||||||||||||||||||||||||||||||||||
|
272. Нахождение логарифма произведения, частного, степени и корня. |
||||||||||||||||||||||||||||||||||||
|
а) Пусть требуется выполнить умножение: 378 • 45,2 |
||||||||||||||||||||||||||||||||||||
|
Попробуем выполнить это действие посредством логарифмов. Найдем в таблицах логарифмы чисел 378 и 45,2. Пусть они будут: 2,5775 и 1,6551 (по основанию 10). Это значит, что |
||||||||||||||||||||||||||||||||||||
|
378 = 102,5775 и 45,2 = 101,6551 |
||||||||||||||||||||||||||||||||||||
|
и следовательно, |
||||||||||||||||||||||||||||||||||||
|
378 . 45,2 = 102,5775 . 101,6551 |
||||||||||||||||||||||||||||||||||||
|
Так как при умножении степеней одного и того же числа показатели этих степеней складываются (какие бы ни были эти показатели), то |
||||||||||||||||||||||||||||||||||||
|
378 . 45,2 = 102,5775 + 1,6551= 104,2326 |
||||||||||||||||||||||||||||||||||||
|
Значит, логарифм произведения 378 . 45,2 есть число 4,2326, получившееся от сложения логарифмов данных сомножителей (по этому логарифму в таблицах найдем и само произведение). |
||||||||||||||||||||||||||||||||||||
|
Положим вообще, что N1 и N2 будут два числа, произведение которых требуется вычислить. Пусть мы нашли в таблицах логарифмы этих чисел х1 и х2. Основание этих логарифмов может быть число 10, но может быть и какое-нибудь другое число, которое мы обозначим а. Тогда мы будем иметь равенства: |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Отсюда видно, что log (N1N2) = x1 + x2 Но x1 - это log N1 , а х2 - это log N2; значит: |
||||||||||||||||||||||||||||||||||||
|
log (N1N2) = log N1 + log N2 , |
||||||||||||||||||||||||||||||||||||
|
т. е. логарифм произведения (по какому угодно основанию) равен сумме логарифмов сомножителей (взятых по тому же основанию). |
||||||||||||||||||||||||||||||||||||
|
Заключение это остается верным и тогда, когда сомножителей будет более 2, так как при умножении степеней одного и того же числа показатели их складываются и тогда, когда, этих степеней будет более 2. |
||||||||||||||||||||||||||||||||||||
|
б) Положим, надо выполнить деление: | ||||||||||||||||||||||||||||||||||||
|
5637 : 26,3. |
||||||||||||||||||||||||||||||||||||
Найдем в таблицах логарифмы этих чисел (напр, по основанию 10). | ||||||||||||||||||||||||||||||||||||
|
5637 = 103,751 и 26,3 = 101,42 |
||||||||||||||||||||||||||||||||||||
|
Следовательно, 5637:26,3=103,751 :101,42 =103,751-1,42 =102,331 |
||||||||||||||||||||||||||||||||||||
|
Отсюда видно, что логарифм частного 5637:26,3 есть число 2,331, получившееся от вычитания логарифма делителя из логарифма делимого. |
||||||||||||||||||||||||||||||||||||
|
Вообще, если |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
и следовательно, |
||||||||||||||||||||||||||||||||||||
|
log(N1 : N2) = x1 - x2 =log N1 - log N2 |
||||||||||||||||||||||||||||||||||||
|
т. е. логарифм частного равен логарифму делимого без логарифма делителя. |
||||||||||||||||||||||||||||||||||||
|
Так как всякая дробь есть частное от деления числителя на знаменатель, то логарифм дроби равен логарифму числителя без логарифма знаменателя. |
||||||||||||||||||||||||||||||||||||
|
Напр.: log 2/3 = log 2 — log 3; Следствие : Поскольку loga1 = 0, то
Таким образом
Логарифмы двух взаимообратных чисел по одному и тому же основанию отличаются друг от друга только знаком. |
||||||||||||||||||||||||||||||||||||
|
в) Если N = ax, то Nn = (ax)n= anx; следовательно: log (Nn) = nx = n log N, т. e. логарифм степени равен показателю этой степени, умноженному на логарифм возводимого в степень числа. |
||||||||||||||||||||||||||||||||||||
|
Напр.: log (15,3)2 = 2 log 15,3; |
||||||||||||||||||||||||||||||||||||
|
г) Так как
т. e. логарифм корня равен логарифму подкоренного числа, деленному на показатель корня. 273. Логарифмирование алгебраического выражения. Логарифмировать алгебраическое выражение значит выразить логарифм его посредством логарифмов отдельных чисел, составляющих это выражение. Выводы предыдущего параграфа позволяют это сделать в применении к произведению, частному, степени и дроби. |
||||||||||||||||||||||||||||||||||||
1) 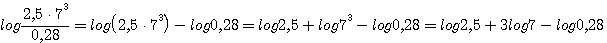 |
||||||||||||||||||||||||||||||||||||
2) 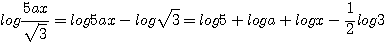 |
||||||||||||||||||||||||||||||||||||
3) 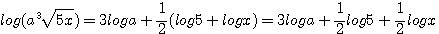 |
||||||||||||||||||||||||||||||||||||
|
274. Замечания. а) Если в выражении, которое требуется вычислить, встречается сумма или разность чисел, то их надо находить без помощи таблиц обыкновенным сложением или вычитанием. Напр.: log (35 +7,24)5 = 5 log (35 + 7,24) = 5 log 42,24. б) Умея логарифмировать выражения, мы можем, обратно, по данному результату логарифмирования найти то выражение, от которого получился этот результат; так, если log х = log a + log b — 3 log с, то легко сообразить, что в) Прежде чем перейти к рассмотрению устройства логарифмических таблиц, мы укажем некоторые свойства десятичных логарифмов, т.е. таких, в которых за основание принято число 10 ( только такие логарифмы употребляются для вычислений). Свойства десятичных логарифмов. 275. а) Так как 101 = 10, 102 = 100, 103 =1000, 104 = 10000 и т. д., то log 10 = 1, log 100 = 2, log 1000 = 3, log 10000 = 4, и т. д. Значит, логарифм целого числа, изображаемого единицею с нулями, есть целое положительное число, содержащее столько единиц, сколько нулей в изображении числа. Таким образом: log 100 000 = 5, log 1000 000 = 6, и т. д. б) Так как
то: log 0,1 = —l; log 0,01 = — 2; log 0,001 == —3; log 0,0001 = — 4, и т. д. Значит, логарифм десятичной дроби, изображаемой единицею с предшествующими нулями, есть целое отрицательное число содержащее столько отрицательных единиц, сколько нулей в изображении дроби, считая в том числе и 0 целых. Таким образом: log 0,00001= — 5, log 0,000001 = —6, и т. д. в) Возьмем целое число, не изображаемое единицею с нулями, напр. 35, или целое число с дробью, напр. 10,7. Логарифм такого числа не может быть целым числом, так как, возвысив 10 в степень с целым показателем (положительным или отрицательным), мы получим 1 с нулями (следующими за 1, или ей предшествующими). Предположим теперь, что логарифм такого числа есть какая-нибудь дробь a/b. Тогда мы имели бы равенства
Но эти равенства невозможны, как как 10а есть 1 с нулями, тогда как степени 35b и 10,7b ни при каком показателе b не могут дать 1 c нулями. Значит, нельзя допустить, чтобы log 35 и log 10,7 были равны дробям. Но из свойств логарифмической функции мы знаем (§ 270, 2), что всякое положительное число имеет логарифм; следовательно, каждое из чисел 35 и 10,7 имеет свой логарифм, и так как он не может быть ни числом целым, ни числом дробным, то он есть число иррациональное и, следовательно, не может быть выражен точно посредством цифр. Обыкновенно иррациональные логарифмы выражают приближенно в виде десятичной дроби с несколькими десятичными знаками. Целое число этой дроби (хотя бы это было „0 целых") называется характеристикой, а дробная часть — мантиссой логарифма. Если, напр., логарифм есть 1,5441, то характеристика его равна 1, а мантисса есть 0,5441. г) Возьмем какое-нибудь целое или смешанное число, напр. 623 или 623,57. Логарифм такого числа состоит из характеристики и мантиссы. Оказывается, что десятичные логарифмы обладают тем удобством, что характеристику их мы всегда можем найти по одному виду числа. Для этого сосчитаем, сколько цифр в данном целом числе, или в целой части смешанного числа, В наших примерах этих цифр 3. Поэтому каждое из чисел 623 и 623,57 больше 100, но меньше 1000; значит, и логарифм каждого из них больше log 100, т. е. больше 2, но меньше log 1000, т. е. меньше 3 (вспомним, что большее число имеет и больший логарифм). Следовательно, log 623 = 2,..., и log 623,57 = 2,... (точки заменяют собою неизвестные мантиссы). Подобно этому найдем:
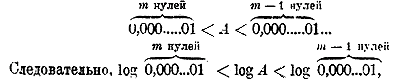
Пусть вообще в данной целом числе, или в целой части данного смешанного числа, содержится m цифр. Так как самое малое целое число, содержащее m цифр, есть 1 с m — 1 нулями на конце, то (обозначая данное число N) можем написать неравенства:
и следовательно, m — 1 < log N < m, и потому log N = (m — 1) + положительная дробь. Значит, характеристика logN = m — 1. Мы видим таким образом, что характеристика логарифма целого или смешанного числа содержит столько положительных единиц, сколько цифр в целой части числа без одной. Заметив это, мы можем прямо писать: log 7,205 = 0,...; log 83 = 1,...; log 720,4 = 2,... и т. п. д) Возьмем несколько десятичных дробей, меньших 1 (т. е. имеющих 0 целых): 0,35; 0,07; 0,0056; 0,0008, и т. п. Таким образом, каждый из этих логарифмов заключен между двумя целыми отрицательными числами, различающимися на одну единицу; поэтому каждый из них равен меньшему из этих отрицательных чисел, увеличенному на некоторую положительную дробь. Напр., log0,0056= —3 + положительная дробь. Предположим, что эта дробь будет 0,7482. Тогда, значит: log 0,0056 = — 3 + 0,7482 (= — 2,2518). Такие суммы, как — 3 + 0,7482, состоящие из целого oтрицательного числа.и положительной десятичной дроби, условились при логарифмических вычислениях писать сокращенно так: 3,7482 ( Такое число читается: 3 с минусом, 7482 десятитысячных.), т. е. ставят знак минус над характеристикой с целью показать, что он относится только к этой характеристике, а не к мантиссе, которая остается положительной. Таким образом, из приведенной выше таблички видно, что log 0,35 == 1,....; log 0,07 = 2,....; log 0,0008 = 4,.... Пусть вообще
т. е. — m < log A < — (m — 1). Так как из двух целых чисел:— m и — (m — 1) меньшее есть — m , то log А = — m + положительная дробь, и потому характеристика log А = — m (при положительной мантиссе). Таким образом, характеристика логарифма десятичной дроби, меньшей 1, содержит в себе столько отрицательных единиц, сколько нулей в изображении десятичной дроби перед первой значащей цифрой, считая в том числе и нуль целых; мантисса же такого логарифма положительна. е) Умножим какое-нибудь число N (целое или дробное — всe равно) на 10, на 100 на 1000..., вообще на 1 c нулями. Посмотрим, как от этого изменится log N. Так как логарифм произведения равен сумме логарифмов сомножителей, то log (N•10) = log N + log 10 = log N + 1; log (N•100) = log N + log 100 = log N + 2; log (N•1000) = log N + log 1000 = log N + 3; и т. д. Когда к log N мы прибавляем какое-нибудь целое число, то это число мы может всегда прибавлять к характеристике, а не к мантиссе. Так, если log N = 2,7804, то 2,7804 + 1 =3,7804; 2,7804 + 2 = 4,7801 и т. п.; или если log N = 3,5649, то 3,5649 + 1 = 2,5649; 3,5649 + 2 = 1,5649, и т. п. Поэтому: От умножения числа на 10, 100, 1000,.., вообще на 1 с нулями, мантисса логарифма не изменяется, а характеристика увеличивается на столько единиц, сколько нулей во множителе. Подобно этому, приняв во внимание, что логарифм частного равен логарифму делимого без логарифма делителя, мы получим: log N/10 = log N— log 10 = log N —1; log N/100 = log N— log 100 = log N —2; log N/1000 = log N— log 1000 = log N —3; и т. п. Если условимся при вычитании целого числа из логарифма вычитать это целое число всегда из характеристики, а мантиссу оставлять без изменения, то можно сказать: От деления числа на 1 с нулями мантисса логарифма не изменяется, а характеристика уменьшается на столько единиц, сколько нулей в делителе. 276. Следствия. Из свойства (е) можно вывести следующие два следствия: а) Мантисса логарифма десятичного числа не изменяется от перенесения в числе запятой, потому что перенесение запятой равносильно умножению или делению на 10, 100, 1000 и т. д. Таким образом, логарифмы чисел: 0,00423, 0,0423, 4,23, 423 отличаются только характеристиками, но не мантиссами (при условии, что все мантиссы положительны). б) Мантиссы чисел, имеющих одну и ту же значащую часть, но отличающихся только нулями на конце, одинаковы: так, логарифмы чисел: 23, 230, 2300, 23 000 отличаются только характеристиками. Замечание. Из указанных свойств десятичных логарифмов видно, что характеристику логарифма целого числа и десятичной дроби мы можем находить без помощи таблиц (в этом заключается большое удобство десятичных логарифмов); вследствие этого в логарифмических таблицах помещаются только одни мантиссы; кроме того, так как нахождение логарифмов дробей сводится к нахождению логарифмов целых чисел (логарифм дроби = логарифму числителя без логарифма знаменателя), то в таблицах помещаются мантиссы логарифмов только целых чисел. Устройство и употребление четырехзначных таблиц. 277. Системы логарифмов. Системою логарифмов называется совокупность логарифмов, вычисленных для ряда последовательных целых чисел по одному и тому же основанию. Употребительны две системы: система обыкновенных или десятичных логарифмов, в которых за основание взято число 10, и система так называемых натуральных логарифмов, в которых за основание (по некоторым причинам, которые уясняются в других отделах математики) взято иррациональное число 2,7182818... Для вычислений употребляются десятичные логарифмы, вследствие тех удобств, которые были нами указаны, когда мы перечисляли свойства таких логарифмов. Натуральные логарифмы называются также Неперовыми по имени изобретателя логарифмов, шотландского математика Непера (1550—1617 гг.), а десятичные логарифмы — Бригговыми по имени профессора Бригга (современника и друга Непера), впервые составившего таблицы этих логарифмов 1). 278. Преобразование отрицательного логарифма в такой, у которого мантисса положительна, и обратное преобразование. Мы видели, что логарифмы чисел, меньших 1, отрицательны. Значит, они состоят из отрицательной характеристики и отрицательной мантиссы. Такие логарифмы всегда можно преобразовать так, что у них мантисса будет положительная, а характеристика останется отрицательной. Для этого достаточно прибавить к мантиссе положительную единицу, а к характеристике — отрицательную (от чего, конечно, величина логарифма не изменится). Если, напр., мы имеем логарифм — 2,0873, то можно написать: — 2,0873 = — 2 — 1 + 1 — 0,0873 = — (2 + 1) + (1 — 0,0873) = — 3 + 0,9127, или сокращенно:
Обратно, всякий логарифм с отрицательной характеристикой и положительной мантиссой можно превратить в отрицательный. Для этого достаточно к положительной мантиссе приложить отрицательную единицу, а к отрицательной характеристике — положительную 2): так, можно написать:
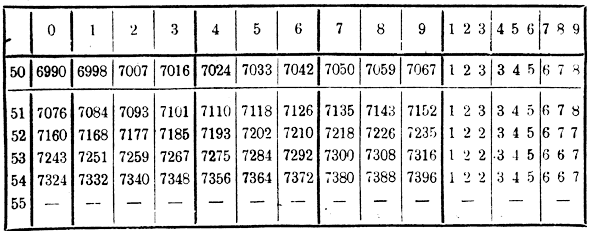
279. Описание четырехзначных таблиц. Для решения большинства практических задач вполне достаточны четырехзначные таблицы, обращение с которыми весьма просто 3). Таблицы эти (с надписью на верху их „логарифмы") помещены в конце этой книги, а небольшая часть их (для объяснения расположения) напечатана на этой странице. В них содержатся мантиссы Логарифмы.
логарифмов всех целых чисел от 1 до 9999 включительно, вычисленные с четырьмя десятичными знаками, причем последний из этих знаков увеличен на 1 во всех тех случаях, когда 5-й десятичный знак должен был бы оказаться 5 или более 5; следовательно, 4-значные таблицы дают приближенные мантиссы с точностью до 1/2 десятитысячной доли (с недостатком или с избытком). Так как характеристику логарифма целого числа или десятичной дроби мы можем, на основании свойств десятичных логарифмов, проставить непосредственно, то из таблиц мы должны взять только мантиссы; при этом надо вспомнить, что положение запятой в десятичном числе, а также число нулей, стоящих в конце числа, не имеют влияния на величину мантиссы. Поэтому при нахождении мантиссы по данному числу мы отбрасываем в этом числе запятую, а также и нули на конце его, если таковые есть, и находим мантиссу образовавшегося после этого целого числа. При этом могут представиться следующие случаи. 1) Целое число состоит из 3-х цифр. Напр., пусть надо найти мантиссу логарифма числа 536. Первые две цифры этого числа, т. е. 53, находим в таблицах в первом слева вертикальном столбце (см. таблицу). Найдя число 53, продвигаемся от него по горизонтальной строке вправо до пересечения этой строчки с вертикальным столбцом, проходящим через ту из цифр 0, 1, 2, 3,... 9, поставленных наверху (и внизу) таблицы, которая представляет собою 3-ю цифру данного числа, т. е. в нашем примере цифру 6. В пересечении получим мантиссу 7292 (т. е. 0,7292), принадлежащую логарифму числа 536. Подобно этому для числа 508 найдем мантиссу 0,7059, для числа 500 найдем 0,6990 и т. п. 2) Целое число состоит из 2-х или из 1-й цифры. Тогда мысленно приписываем к этому числу один или два нуля и находим мантиссу для образовавшегося таким образом трехзначного числа. Напр., к числу 51 приписываем один нуль, от чего получаем 510 и находим мантиссу 7070; к числу 5 приписываем 2 нуля и находим мантиссу 6990 и т. д. 3) Целое число выражается 4 цифрами. Напр., надо найти мантиссу log 5436. Тогда сначала находим в таблицах, как было сейчас указано, мантиссу для числа, изображенного первыми 3-мя цифрами данного числа, т. е. для 543 (эта мантисса будет 7348); затем продвигаемся от найденной мантиссы по горизонтальной строке направо (в правую часть таблицы, расположенную за жирной вертикальной чертой) до пересечения с вертикальным столбцом, проходящим через ту из цифр: 1, 2 3,... 9, стоящих на верху (и в низу) этой части таблицы, которая представляет собою 4-ю цифру данного числа, т. е. в нашем примере цифру 6. В пересечении находим поправку (число 5), которую надо приложить в уме к мантиссе 7348, чтобы получить мантиссу числа 5436; мы получим таким образом мантиссу 0,7353. 4) Целое число выражается 5-ю или более цифрами. Тогда отбрасываем все цифры, кроме первых 4-х, и берем приближенное четырехзначное число, причем последнюю цифру этого числа увеличиваем на 1 в том. случае, когда отбрасываемая 5-я цифра числа есть 5 или больше 5. Так, вместо 57842 мы берем 5784, вместо 30257 берем 3026, вместо 583263 берем 5833 и т. и. Для этого округленного четырехзначного числа находим мантиссу так, как было сейчас объяснено. Руководствуясь этими указаниями, найдем для примера логарифмы следующих чисел: 36,5; 804,7; 0,26; 0,00345; 7,2634; 3456,06. Прежде всего, не обращаясь пока к таблицам, проставим одни характеристики, оставляя место для мантисс, которые выпишем после: log 36,5 = 1,.... log 0,00345 = 3,.... log 804,7 = 2,.... log 7,2634 = 0,.... log 0,26 = 1,.... log 3456,86 = 3,.... Далее по таблицам выставляем прямо мантиссы: log 36,5 = 1,5623; log 0,00345 = 3,5378; log 804,7 = 2,9057; log 7,2634 = 0,8611; log 0,26 = 1,4150; log 3456,86 = 3,5387. 280. Замечание. В некоторых четырехзначных таблицах (напр, в таблицах В. Лорченко и Н. Оглоблина, С. Глазенапа, Н. Каменьщикова) поправки на 4-ю цифру данного числа не помещены. Имея дело с такими таблицами, приходится поправки эти находить при помощи простого вычисления, которое можно выполнять на основании следующей истины: если числа превосходят 100, а разности между ними меньше 1, то без чувствительной погрешности можно принять, что разности между логарифмами пропорциональны разностям между соответствующими числами 4). Пусть, напр., надо найти мантиссу, соответствующую числу 5367. Мантисса эта, конечно, та же самая, что и для числа 536,7. Находим в таблицах для числа 536 мантиссу 7292. Сравнивая эту мантиссу с соседней вправо мантиссой 7300, соответствующей числу 537, мы замечаем, что если число 536 увеличится на 1, то мантисса его увеличится на 8 десятитысячных (8 есть так называемая табличная разность между двумя соседними мантиссами); если же число 536 увеличится на 0,7, то мантисса его увеличится не на 8 десятитысячных, а на некоторое меньшее число х десятитысячных, которое, согласно допущенной пропорциональности, должно удовлетворять пропорции: х : 8 = 0,7 : 1; откуда х = 8•07 = 5,6, что по округлении составляет 6 десятитысячных. Значит, мантисса для числа 536,7 (и следовательно, для числа 5367) будет: 7292 + 6 = 7298. Заметим, что нахождение по двум рядом стоящим в таблицах числам промежуточного числа называется интерполированием. Интерполирование, описанное здесь, называется пропорциональным, так как оно основано на допущении, что изменение логарифма пропорционально изменению числа. Оно называется также линейным, так как предполагает, что графически изменение логарифмической функции выражается прямою линией. 281. Предел погрешности приближенного логарифма. Если число, которого логарифм отыскивается, есть число т о ч н о е, то за предел погрешности его логарифма, найденного но 4-значным таблицам, можно, как мы говорили в § 279, принять 1/2 десятитысячной доли. Если же данное число не точное, то к этому пределу погрешности надо еще добавить предел другой погрешности, происходящей от неточности самого числа. Доказано (мы опускаем это доказательство), что за такой предел можно принять произведение a (d +1) десятитысячных., в котором а есть предел погрешности самого неточного числа в предположении, что в его целой части взяты 3 цифры, a d табличная разность мантисс, соответствующих двум последовательным трехзначным числам, между которыми заключается данное неточное число. Таким образом предел окончательной погрешности логарифма выразится тогда формулой: 1/2 + a (d +1) десятитысячных Пример. Найти log π, принимая за π приближенное число 3,14, точное до 1/2сотой. Перенеся в числе 3,14 запятую после 3-й цифры, считая слева, мы получим трехзначное число 314, точное до 1/2 единицы; значит, предел погрешности неточного числа, т. е. то, что мы обозначили буквой а, есгь 1/2 Из таблиц находим: log 3,14 = 0,4969. Табличная разность d между мантиссами чисел 314 и 315 равна 14, поэтому погрешность найденного логарифма будет менее 1/2 + 1/2 (14 +1) = 8 десятитысячных. Так как о логарифме 0,4969 мы не знаем, с недостатком ли он или с избытком, то можем только ручаться, что точный логарифм π заключается между 0,4969 — 0,0008 и 0,4969 + 0,0008, т. е. 0,4961 < log π < 0,4977. 282. Найти число по данному логарифму. Для нахождения числа по данному логарифму могут служить те же таблицы, по которым отыскиваются мантиссы данных чисел; но удобнее пользоваться другими таблицами, в которых помещены так называемые антилогарифмы, т. е. числа, соответствующие данным мантиссам. Таблицы эти, обозначенные надписью сверху „антилогарифмы", помещены в конце этой книги вслед за таблицами логарифмов; небольшая часть их помещена на этой странице (для объяснения).
Пусть дана 4-значная мантисса 2863 (на характеристику не обращаем внимания) и требуется найти соответствующее целое число. Тогда, имея таблицы антилогарифмов, надо пользоваться ими совершенно так же, как было раньше объяснено для нахождения мантисс по данному числу, а именно: первые 2 цифры мантиссы мы находим в первом слева столбце. Затем продвигаемся от этих цифр по горизонтальной строке вправо до пересечения с вертикальным столбцом, идущим от 3-й цифры мантиссы, которую надо искать в верхней строке (или в нижней). В пересечении находим четырехзначное число 1932, соответствующее мантиссе 286. Затем от этого числа продвигаемся дальше по горизонтальной строке направо до пересечения с вертикальным столбцом, идущим от 4-й цифры мантиссы, которую надо найти наверху (или внизу) среди поставленных там цифр 1, 2, 3,... 9. В пересечении мы находим поправку 1, которую надо приложить (в уме) к найденному раньше числу 1032, чтобы получить число, соответствующее мантиссе 2863. Таким образом, число это будет 1933. После этого, обращая внимание на характеристику, надо в числе 1933 поставить занятую на надлежащем месте. Например: если log x = 3,2863, то х = 1933, „ log x = 1,2863, „ х = 19,33, ,, log x = 0,2&63, „ х = 1,933, „ log x = 2,2863, „ х = 0,01933 и т.п. Вот еще примеры: log x = 0,2287, х = 1,693, log x = 1,7635, х = 0,5801, log x = 3,5029, х = 3184, log x = 2,0436, х = 0,01106. Если в мантиссе указано 5 или более цифр, то берем только первые 4 цифры, отбрасывая остальные (и увеличивая 4-ю цифру на 1, если 5-я цифра есть пять или более). Напр., вместо мантиссы 35478 берем 3548, вместо 47562 берем 4756. 283. Замечание. Поправку на 4-ю и следующие цифры мантиссы можно находить и посредством интерполирования. Так, если мантисса будет 84357, то, найдя число 6966, соответствущее мантиссе 843 мы можем рассуждать далее так :: если мантисса увеличивается на 1 (тысячную), т. е. сделаетоя 844, то число, как видно из таблиц, увеличится на 16 единиц; если же мантисса увеличится не на 1 (тысячную), а на 0,57 (тысячной), то число увеличится на х единиц, причем х должно удовлетворять пропорции: х : 16 = 0,57 : 1, откуда х = 16•0,57 = 9,12. Значит, искомое число будет 6966+ 9,12 = 6975,12 или (ограничиваясь только четырьмя цифрами) 6975. 284. Предел погрешности найденного числа. Доказано, что в том случае, когда в найденном числе запятая стоит после 3-й слева цифры, т. е. когда характеристика логарифма есть 2, за предел погрешности можно принять сумму
где а есть предел погрешности логарифма (выраженный в десятитысячных долях), по которому отыскивалось число, и d — разность между мантиссами двух трехзначных последовательных чисел, между которыми заключается найденное число (с запятой после 3-й цифры слева). Когда характеристика будет не 2, а какая-нибудь иная, то в найденном числе запятую придется перенести влево или вправо, т. е. разделить или умножить число на некоторую степень 10. При этом погрешность результата также разделится или умножится на ту же степень 10. Пусть, например, мы отыскиваем число по логарифму 1,5950, о котором известно, чго он точен до 3 десятитысячных; значит, тогда а = 3. Число, соответствующее этому логарифму, найденное по таблице антилогарифмов, есть 39,36. Перенеся запятую после 3-й цифры слева, будем иметь число 393,6, заключающееся между 393 и 394. Из таблиц логарифмов видим, что разность между мантиссами, соответствующими этим двум числам, составляет 11 десятитысячных; значит d = 11. Погрешность числа 393,6 будет меньше
Значит, погрешность числа 39,36 будет меньше 0,05. 285. Действия над логарифмами с отрицательными характеристиками. Сложение и вычитание логарифмов не представляют никаких затруднений, как это видно из следующих примеров:
Не представляет никаких затруднений также и умножение логарифма на положительное число, напр.:
В последнем примере отдельно умножена положительная мантисса на 34, затем отрицательная характеристика на 34. Если логарифм о отрицательной характеристикой и положительной мантиссой умножается на отрицательное число, то поступают двояко: или предварительно данный логарифм обращают в отрицательный, или же умножают отдельно мантиссу и характеристику и результаты соединяют вместе, например: 3,5632 • ( — 4) = — 2,4368 • (— 4) = 9,7472; 3,5632 •( — 4) = + 12 — 2,2528 = 9,7472. При делении могут представиться два случая: 1) отрицательная характеристика делится и 2) не делится на делитель. В первом случае отдельно делят характеристику и мантиссу: 10,3784 : 5 = 2,0757. Во втором случае прибавляют к характеристике столько отрицательных единиц, чтобы образовавшееся число делилось на делитель; к мантиссе прибавляют столько же положительных единиц: 3,7608 : 8 = ( — 8 + 5,7608) : 8 = 1,7201. Это преобразование надо совершать в уме, так что действие располагается так:
286. Замена вычитаемых логарифмов слагаемыми. При вычислении какого-нибудь сложного выражения помощью логарифмов приходится некоторые логарифмы складывать, другие вычитать; в таком случае, при обыкновенном способе совершения действий, находят отдельно сумму слагаемых логарифмов, потом сумму вычитаемых и из первой суммы вычитают вторую. Напр., если имеем: log х = 2,7305 — 2,0740 + 3,5464 — 8,3589, то обыкновенное выполнение действий расположится так:
Есть однако возможность заменить вычитание сложением. Так:
Теперь можно расположить вычисление так:
287. Примеры вычислений. Пример 1. Вычислить выражение:
если А = 0,8216, В = 0,04826, С= 0,005127 и D = 7,246. Логарифмируем данное выражение: log х = 1/3 log A + 4 log В — 3 log С — 1/3 log D Теперь, для избежания излишней потери времени и для уменьшения возможности ошибок, прежде всего расположим все вычисления, не исполняя пока их и не обращаясь, следовательно, к таблицам:
После этого берем таблицы и проставляем логарифмы на оставленных свободных местах:
Прeдел погрешности. Сначала найдем предел погрешности числа x1 = 194,5, равный:
Значит, прежде всего надо найти а, т. е. предел погрешности приближенного логарифма, выраженный в десятитысячных долях. Допустим, что данные числа А, В, С и D все точные. Тогда погрешности в отдельных логарифмах будут следующие (в десятитысячных долях): в logА.......... 1/2 в 1/3 log A.........1/6 + 1/2 = 2/3 (1/2 прибавлена потому, что при делении на 3 логарифма 1,9146 мы округлили частное, отбросив 5-ю цифру его, и, следовательно, сделали еще ошибку,меньшую 1/2 десятитысячной).
Теперь находим предел погрешности логарифма: а = 2/3 + 2 + 3/2 + 1/6 = 4 1/3 (десятитысячных). Определим далее d . Так как x1 = 194,5, то 2 целых последовательных числа, между которыми заключается x1 будут 194 и 195. Табличная разность d между мантиссами, соответствующими этим числам, равна 22. Значит, предел погрешности числа x1 есть:
Так как x = x1 : 10, то предел погрешности в числе x равен 0,3:10 = 0,03. Таким образом, найденное нами число 19,45 разнится от точного числа менее, чем на 0,03. Так как мы не знаем, с недостатком или с избытком найдено наше приближение, то можем только ручаться, что 19,45 + 0,03 > х > 19,45 — 0,03, т. е. 19,48 > х > 19,42, и потому, если примем х =19,4, то будем иметь приближение с недостатком с точностью до 0,1. Пример 2. Вычислить: х = (— 2,31)3 5√72 = — (2,31)3 5√72. Так как отрицательные числа не имеют логарифмов, то предварительно находим: х' = (2,31)3 5√72 по разложению: log х' = 3 log 2,31 + 1/5 log72. После вычисления окажется: х' = 28,99; следовательно, x = — 28,99. Пример 3. Вычислить:
Сплошного логарифмирования здесь применить нельзя, так как под знаком корня стоит с у м м а. В подобных случаях вычисляют формулу по частям. Сначала находим N = 5√8, потом N1 = 4√3; далее простым сложением определяем N + N1, и, наконец, вычисляем 3√N + N1; окажется: N = 1,514, N1 = 1,316; N + N1 = 2,830. log x = log 3√2,830 = 1/3 log 2,830 = 0,1506; x = 1,415. Показательные и логарифмические уравнения. 288. Показательными уравнениями называются такие, в которых неизвестное входит в показатель степени, а логарифмическими — такие, в которых неизвестное входит под знаком log. Такие уравнения могут быть разрешаемы только в частных случаях, причем приходится основываться на свойствах логарифмов и на том начале, что если числа равны, то равны и их логарифмы, и, обратно, если логарифмы равны, то равны и соответствующие им числа. Пример 1. Решить уравнение: 2x = 1024. Логарифмируем обе части уравнения:
Пример 2. Решить уравнение: a2x — ax = 1. Положив ax = у, получим квадратное уравнение: y2 — у — 1 = 0,
Так как 1—√5 < 0, то последнее уравнение невозможно (функция ax всегда есть число положительное), а первое дает:
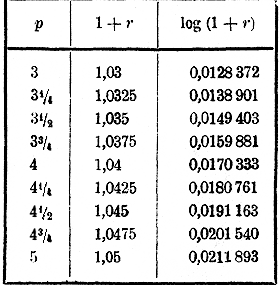
Пример 3. Решить уравнение: log (а + x) + log (b + х) = log (с + x). Уравнение можно написать так: log [(а + x) (b + х)] = log (с + x). Из равенства логарифмов заключаем о равенстве чисел: (а + x) (b + х) = с + x. Это есть квадратное уравнение, решение которого не представляет затруднений. Сложные проценты, срочные уплаты и срочные взносы. 289. Основная задача на сложные проценты. В какую сумму обратится капитал а рублей, отданный в рост по р сложных процентов, по прошествии t лет (t — целое число)? Говорят, что капитал отдан по сложным процентам, если принимаются во внимание так называемые „проценты на проценты", т. е. если причитающиеся на капитал процентные деньги присоединяются в конце каждого года к капиталу для наращения их процентами в следующие годы. Каждый рубль капитала, отданного по р %, в течение одного года принесет прибыли p/100 рубля, и, следовательно, каждый рубль капитала через 1 год обратится в 1+ p/100 рубля (напр., если капитал отдан по 5% , то каждый рубль его через год обратится в 1+ 5/100, т. е. в 1,05 рубля). Обозначив для краткости дробь p/100 одною буквою, напр, r, можем сказать, что каждый рубль капитала через год обратится в 1 + r рублей; следовательно, а рублей обратятся через 1 год в а(1 + r) руб. Еще через год, т. е. через 2 года от начала роста, каждый рубль из этих а (1 + r) руб. обратится снова в 1 + r руб.; значит, весь капитал обратится в а (1 + r) 2 руб. Таким же образом найдем, что через три года капитал будет а (1 + r) 3, через четыре года будет а (1 + r) 4,... вообще через t лет, если t есть целое число, он обратится в а (1 + r) t руб. Таким образом, обозначив через А окончательный капитал, будем иметь следующую формулу сложных процентов: А = а (1 + r) t где r = p/100. Пример. Пусть a =2 300 руб., p = 4, t =20 лет; тогда формула дает: r = 4/100= 0,04; А = 2 300 • (1,04)20. Чтобы вычислить А, применяем логарифмы: log a = log 2 300 + 20 log 1,04 = 3,3617 + 20 • 0,0170 = 3,3617+0,3400 = 3,7017. A = 5031 рубль. Замечание. В этом примере нам пришлось log 1,04 умножить на 20. Так как число 0,0170 есть приближенное значение log 1,04 с точностью до 1/2 десятитысячной доли, то произведение этого числа на 20 будет точно только до 1/2 • 20, т. е. до 10 десятитысячных =1 тысячной. Поэтому в сумме 3,7017 мы не можем ручаться не только за цифру десятитысячных, но и за цифру тысячных. Чтобы в подобных случаях можно было получить большую точность, лучше для числа 1 + r брать логарифмы не 4-значные, а с большим числом цифр, напр. 7-значные. Для этой цели мы приводим здесь небольшую табличку, в которой выписаны 7-значные логарифмы для наиболее употребительных значений р.
290. Основная задача на срочные уплаты. Некто занял а рублей по р % с условием погасить долг, вместе с причитающимися на него процентами, в t лет, внося в конце каждого года одну и ту же сумму. Какова должна быть эта сумма? Сумма x, вносимая ежегодно при таких условиях, называется срочною уплатою. Обозначим опять буквою r ежегодные процентные деньги с 1 руб., т. е. число p/100. Тогда к концу первого года долг а возрастает до а (1 + r), аза уплатою х рублей он сделается а (1 + r)—х. К концу второго года каждый рубль этой суммы снова обратится в 1 + r рублей, и потому долг будет [а (1 + r)—х](1 + r) = а (1 + r)2 — x(1 + r), а за уплатою x рублей окажется: а (1 + r)2 — x(1 + r) — х. Таким же образом убедимся, что к концу 3-го года долг будет а (1 + r)3 — x(1 + r)2 — x(1 + r) — x, и вообще и концу t-го года он окажется: а (1 + r)t — x(1 + r)t —1 — x(1 + r)t —2... — x(1 + r) — x, или а (1 + r)t — x [ 1 + (1 + r) + (1 + r)2 + ...+ (1 + r)t —2+ (1 + r)t —1] Многочлен, стоящий внутри скобок [], представляет сумму членов геометрической прогрессии; у которой первый член есть 1, последний (1 + r)t —1, а знаменатель (1 + r). По формуле для суммы членов геометрической прогрессии (отдел 10 глава 3 § 249) находим:
и величина долга после t-ой уплаты будет:
По условию задачи, долг в конце t-го года должен равняться 0; поэтому:
При вычислении этой формулы срочных уплат помощью логарифмов мы должны сначала найти вспомогательное число N = (1 + r)t по логарифму: log N= t log (1 + r); найдя N, вычтем из него 1, тогда получим знаменатель формулы для х, после чего вторичным логарифмированием найдем: log х = log a + log N + log r — log (N — 1). 291. Основная задача на срочные взносы. Некто вносит в банк в начале каждого года одну и ту же сумму а руб. Определить, какой капитал образуется из этих взносов по прошествии t лет, если банк платит по р сложных процентов. Обозначив через r ежегодные процентные деньги с 1 рубля, т. е. p/100, рассуждаем так: к концу первого года капитал будет а (1 + r); в начале 2-го года к этой сумме прибавится а рублей; значит, в это время капитал окажется а (1 + r) + a . К концу 2-го года он будет а (1 + r)2 + а (1 + r); в начале 3-го года снова вносится а рублей; значит, в это время капитал будет а (1 + r)2 + а (1 + r) + а; к концу 3-го он окажется а (1 + r)3 + а (1 + r)2 + а (1 + r) Продолжая эти рассуждения далее, найдем, чтo к концу t-го года искомый капитал A будет:
Такова формула срочных взносов, делаемых в начале каждого года. Ту же формулу можно получить и таким рассуждением:. первый взнос в а рублей, находясь в банке t лет, обратится, согласно формуле сложных процентов, в а (1 + r)t руб. Второй взнос, находясь в банке одним годом меньше, т. е. t — 1 лет, обратится в а (1 + r)t— 1 руб. Подобно этому третий взнос даст а (1 + r)t— 2 и т. д., и, наконец, последний взнос, находясь в банке только 1 год, обратится в а (1 + r) руб. Значит, окончательный капитал A руб. будет: A = а (1 + r)t + а (1 + r)t— 1 + а (1 + r)t— 2+ . . . + а (1 + r), что, после упрощения, дает найденную выше формулу. При вычислении помощью логарифмов этой формулы надо поступить так же, как и при вычислении формулы срочных уплат, т. е. сначала найти число N = (1 + r)t по его логарифму: log N= t log (1 + r), затем число N— 1 и уже тогда логарифмировить формулу: log A = log a + log (1 + r) + log (N — 1) — 1оg r Замечание. Если бы срочный взнос в а руб. производился не в начале, а в конце каждого года (как, напр., вносится срочная уплата х для погашения долга), то, рассуждая подобно предыдущему, найдем, что к концу t-го года искомый капитал А' руб. будет (считая в том числе и последний взнос а руб., не приносящий процентов): A' = а (1 + r)t— 1 + а (1 + r)t— 2+ . . . + а (1 + r) + а что равно:
т. е. А' оказывается в (1 + r) pаз менее А, что и надо было ожидать, так как каждый рубль капитала А' лежит в банке годом меньше, чем соответствующий рубль капитала А. |
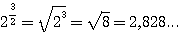
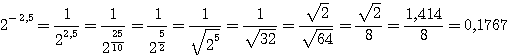
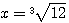
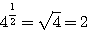 ;
;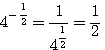
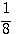
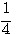
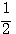
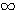
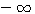
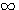
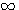
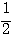
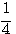
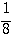
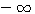
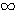
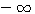
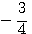
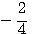
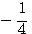
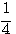
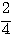
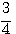
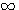
 , поднимаются все выше и выше неограниченно.
, поднимаются все выше и выше неограниченно.  до 0; с возрастанием числа от 1 до
до 0; с возрастанием числа от 1 до 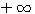 логарифм его возрастает от 1 до
логарифм его возрастает от 1 до 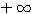 Из этого между прочим следует, что большему числу соответствует больший логарифм (при основании, меньшем 1 (a <1) , заключение было бы обратное).
Из этого между прочим следует, что большему числу соответствует больший логарифм (при основании, меньшем 1 (a <1) , заключение было бы обратное).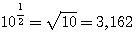 , что меньше 5, a
, что меньше 5, a 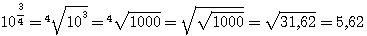 , что больше 5.
, что больше 5.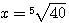
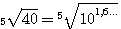
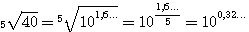
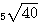
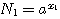 ;
; 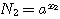 ; следовательно
; следовательно 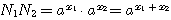
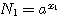 ;
; 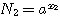 ; то
; то 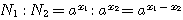
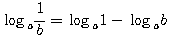
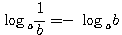
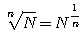 то, применяя правило о логарифме степени, получим:
то, применяя правило о логарифме степени, получим: