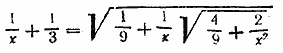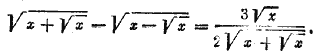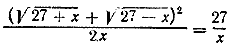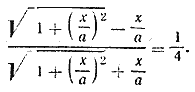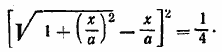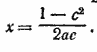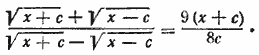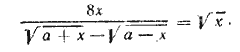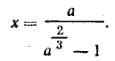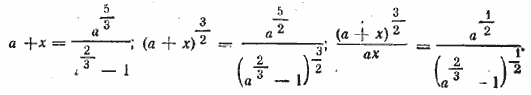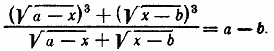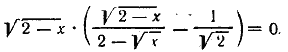|
|
ГЛАВА 3 АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ Ответы и решения Уединим один из радикалов, например первый. Получим √y +2 = 2 + √y — 6 . Возведем обе части в квадрат. После приведения подобных членов и сокращения на 4 будем иметь √y — 6 = 1, откуда у =7. Проверка показывает, что этот корень годен. Замечание 1. Здесь и в дальнейшем мы считаем корни квадратные и вообще корни четных степеней арифметическими. См. предварительные замечания . Относительно корней нечетных степеней см. примечание к задаче 451. Замечание 2. Проверка делается для того, чтобы обнаружить лишние корни (они могут получиться при возведении обеих частей уравнения в квадрат). В данной задаче лишних корней нет. Но возьмем уравнение √y +2 + √y — 6 = 2, отличающееся от данного только знаком. Решая его тем же способом, получим √y — 6 = —1. Возведя в квадрат, найдем тот же корень у =7. Он не годится; взятое уравнение вовсе не имеет решения. Здесь можно было бы обойтись и без проверки, так как и без того видно, что √y — 6 не может равняться —1 (см. замечание 1). Но в других случаях (см. задачи 426 и 432) без проверки обойтись нельзя. Ответ у =7 __________________________________________________ Решается, как предыдущая задача. Ответ х = 6 __________________________________________________ Уединив первый радикал, возведя в квадрат и упростив, получим х—1 = 2√x — 1 Снова возведя в квадрат, находим (х—1)2—4(х—1) = 0. Это уравнение можно разделить на х—1 , предварительно учтя, что х=1 есть один из корней. Тогда найдем другой корень х = 5. Можно также раскрыть скобки и решить квадратное уравнение. Проверка показывает, что оба корня годятся. Ответ x1 = l, x2=5. __________________________________________________ Поступая как в предыдущей задаче, найдем х+22 = = 7√3x — 2, а отсюда Ответ х = 6. __________________________________________________ Решается, как предыдущая задача. Из двух корней x1= —1; x2= 3 второй лишний. Замечание. х = 3 есть корень уравнения — √x + 1 + √2x + 3 Ответ х = —1 __________________________________________________ Ответ x1 =34; x2=2. __________________________________________________ Ответ х = 4. __________________________________________________ Возводим в квадрат. Получаем уравнение х √x2+ 24 — x2 — 2х = 0. Оно распадается на два уравнения: х =0 и √x2+ 24 — x — 2 = 0. Второе дает x =5. Выполняем проверку. Ответ x1= 0; x2=5. __________________________________________________ Данное уравнение приводим к виду
Возводим в квадрат и помножаем на x2 (при умножении на x2 есть опасность ввести лишний корень х=0). Получаем уравнение
Снова возводим в квадрат. Ответ х = 3/4 __________________________________________________ Помножив обе части уравнения на √(x + 2) (x + 3) , получим √(x — 5) (x + 3) + √(x — 4) (x + 2) =7. Поступая как в задаче 423, найдем √(x — 4) (x + 2) = 4. Отсюда получим два корня x1 = 6, x2=—4. Проверка показывает, что x2 не годится, получается неверное равенство 7/2√ 2 = —7/2√ 2 Ответ х = 6 __________________________________________________ Освобождаемся от знаменателя. Получаем √x2— 16 + √x2 — 9 = 7. Это уравнение имеет два корня х=5 и х=—5. Однако при х=—5 выражение √x— 3 не имеет действительного значения (см. замечание 1 к задаче 423). Ответ х =5. __________________________________________________ Приведем левую часть уравнения к общему знаменателю^
Отсюда 3(х +1) = 5√х(х+ 1). После возведения в квадрат получаем 9(х + 1)2—25(х + 1)х =0 (х + 1) [9(х + 1)—25х]=0. Ответ x1 = — 1; x2 = 9/16 __________________________________________________ Решается, как предыдущая задача. Ответ x1=2; x2= —1,6. __________________________________________________ Возводим обе части данного уравнения в квадрат. После тождественных преобразований получим √28— x = √7. При возведении в квадрат есть опасность ввести посторонний корень, удовлетворяющий уравнению, отличающемуся от данного
знаком правой части. Уравнение √28— x = √7 имеет единственный корень х=21. Он не посторонний, так как Ответ x = 21. __________________________________________________ Перепишем уравнение так:
Освободимся от знаменателя; при этом есть опасность ввести лишний корень х = 0 (так как знаменатель обращается в нуль при х = 0). Других лишних корней быть не может, так как х = 0 есть единственный корень уравнения После упрощения получаем уравнение 2х — 2√x2— x — √x = 0, одним из корней которого является х = 0. Однако этот корень лишний, так как при х = 0 правая часть исходного уравнения теряет смысл. Выносим за скобку √x √x (2 √x — 2 √x — l — l) = 0 Решая уравнение √x (2 √x — 2 √x — l — l) = 0 (см. решение задачи 423), находим Ответ х = 25/16 __________________________________________________ Сначала освобождаемся от иррациональности в знаменателе. Умножаем для этого числитель и знаменатель на √27 + x + √27 — х. получим
или, после упрощений,
Отсюда находим х = ±27. Оба корня годятся. Ответ х = ±27 __________________________________________________ Уединив радикал, возведем обе части уравнения в квадрат. Будем иметь x2 — аx = — x√x2+ а2 Это уравнение имеет корень x = 0. Для отыскания других корней разделим обе части уравнения на х (это можно сделать, так как теперь x =/= 0). После этого снова возведем обе части в квадрат. Получим х = 3/4 а. При проверке можно прийти к ошибочному заключению, что значения Когда а = —1, данное уравнение имеет вид
Ни х = 0, ни х = 3/4 а = — 3/4 а не удовлетворяют этому уравнению (оно не имеет решений). Так же будет при любом другом отрицательном значении а. Источник ошибки в том, что величина √а2 считается равной а, тогда как это верно лишь при а > 0. При а < 0 мы имеем √а2 = — a; например, √(— 3)2 = — (— 3). Правильная общая формула (см. предварительное замечание, п. 3) такова: √а2 = | а |. Пользуясь этой формулой, мы найдем, что при х = 0 (когда левая часть уравнения обращается в нуль) правая часть равна а —√а2 = а — | а |. При а > 0 это выражение тоже равно нулю, но при а < 0 оно равно 2а. Следовательно, если а > 0, то значение х = 0 есть корень уравнения; если же а < 0, то х = 0 не является корнем. То же относится и к значению х = 3/4 а. Ответ Если а > 0, то x1 = 0, x2 = 3/4 а; если1 а < 0, уравнение не имеет решений. __________________________________________________ Записанное без степеней с отрицательным показателем данное уравнение имеет вид Первый способ Освобождается от знаменателя: Второй способ. Уничтожаем иррациональность в знаменателе:
Выражение, стоящее в скобках, не может быть отрицательным; поэтому
Возводим в квадрат: Ответ х = 3/4а __________________________________________________ Решается, как предыдущая задача. Применяя второй способ, найдем
Выражение
Возводим в квадрат. Получаем П р о в е р к а. Подставляя
Учитывая, что величина с2+1 всегда положительна, находим
Дальнейшие вычисления показывают, что данное уравнение всегда удовлетворяется. Ответ __________________________________________________ Вынесем за скобки в числителе и знаменателе левой части выражение √х+с и сократим на него дробь / Сокращая на √х+с , мы предполагаем, что х =/= с. Если бы, решив полученное уравнение, мы нашли х =—с, то это значение не было бы корнем данного уравнения. Однако из дальнейшего видно, что такого корня мы не получаем. После сокращения получим
Уничтожим иррациональность в знаменателе. После упрощений найдем.8√х2— с2 = х + 9с. Отсюда x = 5c/3 или х= — 29/21 с. Проверка показывает, что оба эти значения удовлетворяют уравнению при с > 0 и не удовлетворяют при с < 0. Ответ При с > 0 имеем x1 =5/3 с и x2 = — 29/21 с ; при с < 0 уравнение не имеет решений. __________________________________________________ Первое подкоренное выражение преобразуем так: х + 3 — 4√х — 1 = (х—1) — 4√х — 1+4= (√х — 1—2)2. Аналогично второе подкоренное выражение равно (√х — 1—3)2 Данное уравнение принимает вид |√х — 1—2| + |√х — 1—3|= 1 (A) (см. предварительное замечание , п. 3). Возможны три случая: 1) √х — 1 > 3; 2) √х — 1 < 2; 3) 2 <√х — 1 < 3. В первом случае уравнение (А) принимает вид: √х — 1—2 + √х — 1—3 — 1, или √х — 1 = 3. Этот результат не согласуется с условием √х — 1>3. Во втором случае уравнение (А) принимает вид: — (√х — 1—2) — (√х — 1—3) = 1, или √х — 1= 2. Этот результат также не согласуется с условием √х — 1< 2. Остается третий случай, когда уравнение (А) приникает вид: (√х — 1—2) — (√х — 1—3) = 1 . (В) Это равенство является тождеством, следовательно, уравнение (А) удовлетворяется при всех х, для которых 2 <√х — 1 < 3 Так как величина √х — 1>0, то все три части неравенства можно возвести в квадрат, после чего находим 5 < x < 10, т. е. решения данного уравнения содержатся в границе между 5 и 10 (включая и значения 5 и 10). Все они являются решениями данного уравнения, так как подходят под случай 3, когда данное уравнение (А) обращается в тождество (В). Ответ 5 < x < 10 __________________________________________________ Возведем обе части уравнения в квадрат, перенесем все члены в одну сторону и вынесем за скобки √a + x √a + x (4 √a + x + 4 √a — x — √x ) = 0. Это уравнение распадается на два. Из первого√a + x = 0 находим х = — а. Проверка показывает, что при а > 0 это значение удовлетворяет данному уравнению. При а<0 уравнение теряет смысл (так как √a — x становится мнимым). Второе уравнение есть 4 ( √a + x + √a — x ) = √x . Если его решать, как в задачах 425 - 429, то получим (кроме заведомо лишнего корня x = 0) х = 64a/1025 . Проверка покажет, что и это — лишний корень, так что второе уравнение вовсе не имеет решений. В этом проще убедиться, если применить следующий способ решения. Переведем иррациональность в знаменатель (помножив и разделив √a + x + √a — x на сопряженное выражение √a + x — √a — x ). Получим
Разделив на √x (что возможно без потери корней, так как x = 0 не есть корень), получим √a + x — √a — x = 8 √x. Вычитая это уравнение из полученного выше √a + x + √a — x = 1/4√x находим 2 √a — x = — 31/4√x Но это равенство невозможно, так как левая часть есть положительное число, а правая — отрицательное. Если бы, не обратив на это внимания мы возвели обе части в квадрат, то получили бы лишний корень х = 64/1025 а' Ответ Если а положительно, то х =—а; если а отрицательно, то уравнение не имеет решения. __________________________________________________ Здесь с успехом можно применить перевод иррациональности в знаменатель (см. предыдущую задачу). Ответ х = 0. __________________________________________________ Ответ x1 = a; x2 = —b. __________________________________________________ Ответ При а < 1 уравнение не имеет решений. __________________________________________________ Данное уравнение можно представить в виде
или
Возводим в степень 2/3. Получаем Отсюда Проверка:
Ответ __________________________________________________ Полагаем 4√x = z. Тогда √x = ( 4√x )2 = z2 Уравнение примет вид z2 + z —12 = 0. Отсюда z1 = 3, z2= — 4. Так как 4√x должен быть положительным числом, то второй корень лишний. Ответ х =81. __________________________________________________ Полагаем Ответ х =17. __________________________________________________ 451. Здесь и в дальнейшем корни кубические и вообще корни нечетных степеней мы не считаем арифметическими, допуская, что подкоренное число может быть и отрицательным (но обязательно действительным). Значение корня мы также считаем действительным числом.
Возводим обе части уравнения в куб. Получим √10 + 2х + √15 —2х = 7. Здесь можно уединить один из радикалов, а можно и на уединять. Ответ x1 = 3; .x2 = — 1/2 __________________________________________________ Возведем обе части уравнения в куб, применив формулу (a+b)3=a3+3ab(a+b)+b3. Получим х + 33√х(2х — 3) [3√х + 3√2х — 3 ] + 2х — 3 = 12 (х — 1). Выражение в квадратных скобках в силу заданного уравнения можно заменить выражением 3√12 (х — 1). Получаем 3√х(2х — 3)• 12 (х — 1) = 3 (х — 1). Возводим в куб. Перенося члены в одну сторону, найдем (х—1) [12х(2х—3)— 27(х—1)2]=0. Это уравнение распадается на два: х — 1 = 0 и 12х(2х—3) —27 (х— 1)2 = 0 Найденные корни проверяем. Ответ x1= l , x2=3. __________________________________________________ Задача решается, как предыдущая. Ответ x1= a, x2= b, __________________________________________________ Полагаем 3√х = z ; тогда 3√х2 = z2 Подставив в исходное уравнение, получаем 2z2 + z —3 = 0, откуда z1 = 1; z2= — 3/2 Ответ x1 = 1; x2= — 7/8 __________________________________________________ Решается, как предыдущая задача. Ответ z1 = 64; z2= — 125/8 __________________________________________________ Полагаем 6√а + х = z; тогда √а + х = z3 и 3√а + х = z2 Ответ x1= —а; x2=1—а. __________________________________________________ Полагаем Второе решение отбрасываем, как отрицательное (см. замечание 1 к задаче 423 ). Для определения х получим уравнение Ответ х = 7. __________________________________________________ Ответ x = ±5. __________________________________________________ Положим 3√х = z тогда 3√х2 = z2 и х = z3. Получаем:
Сокращаем первую дробь на z2—1, вторую на z +1. Получаем z2— z —2 = 0. Но сокращение первой дроби законно только при условии, что z2—1=/= 0, а второй — только при условии, что z +1=/= 0. Между тем из двух корней z1=2 и z2=—1 второй дает z +1= 0. Он не годится, так как при z =—1 имеем х =—1, и левая часть данного уравнения теряет смысл. Ответ x = 8. __________________________________________________ Полагая √х = z, преобразуем уравнение к виду
Сокращаем дробь на z + 2 (см. объяснение к предыдущей задаче). Получаем z2— z —6=0, откуда z1 = 3; z2= —2. Второй корень не годится, потому что, во-первых, выражение Ответ x = 9. __________________________________________________ Здесь введение вспомогательного неизвестного, которым, мы пользовались в предыдущих задачах, не приводит к цели. Представляем уравнение в виде
Сокращаем дробь на √а—х + √х — b (сокращение законно, так как это число не может равняться нулю). После упрощений получаем √(а — х)(х — b) = 0. Ответ x1= а; x2= b. __________________________________________________ Заданное уравнение представим в виде
Это уравнение распадается на два: первое √2—х = 0;его корень x1 =2; второе после освобождения от знаменателя будет √2(2—х) = 2 — √х. Его корни x2 = 0; x3 = 16/9. Ответ x1 =2; x2 = 0; x3 = 16/9. __________________________________________________ Ответ x =81. __________________________________________________ Если, уединив радикал, возведем обе части полученного уравнения в квадрат, то получим уравнение 4-й степени. Но в данном случае можно применить искусственный прием. Перепишем, уравнение в виде √х2 — 3х + 5 + х2 — 3х + 5 = 12. Полагая √х2 — 3х + 5 = z, получаем z2 + z—12 = 0. Берем только положительный корень 2 = 3. Ответ x1 = 4; x2= — 1. __________________________________________________ Можно применить тот же прием, что в предыдущей задаче. Однако заранее можно сказать, что уравнение не имеет решений. Действительно, величина 3х2 + 5х + l при всяком х больше, чем 3х2 + 5х —8. Поэтому √3х2 + 5х + l > √3х2 + 5х — 8 , значит, левая часть данного уравнения при всяком x отрицательна и, следовательно, не может равняться единице. Ответ Уравнение не имеет решений. __________________________________________________ Обозначим через z одно из подкоренных выражений — удобнее всего положить √ z + 2 + √ z — 2 = √ 2z. Освобождаясь от радикалов, находим z2 = 4. Годится только корень z=2 (при z=—2 два подкоренных выражения отрицательны). Решаем уравнение у2+4у+6 =2. Проверяем. Ответ у = —2. __________________________________________________ |
(см. решение задачи 
Левая часть положительна, значит, поло-жительна и правая часть. Возводим в квадрат:
Отсюда 
(значение —3/4 исключается, ибо x/a >0)
или 
, откуда 
.
всегда положительно. Поэтому 
, или, что то же 
находим
, т. е. при с > 0 имеем 
при с < 0 имеем 
(при a > l).
. 
. Дальше решается, как предыдущая задача.
; тогда 
и уравнение после ряда преобразований примет вид 12z2—7z—12 = 0; отсюда z1 = 4/3; z2= — 3/4
теряет смысл
и, во-вторых, z не может быть отрицательным числом. 
