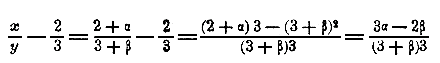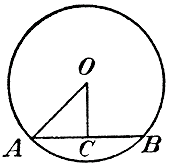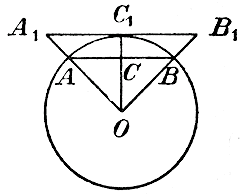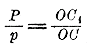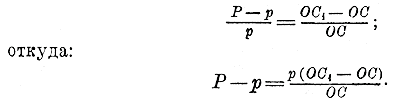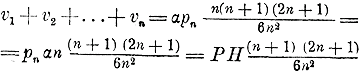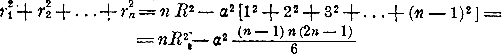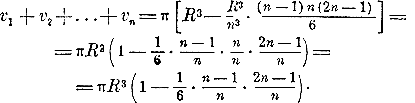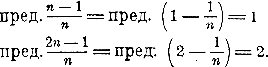| АЛГЕБРА В НАЧАЛО | ||||||||||
|
ОТДЕЛ ЧЕТЫРНАДЦАТЫЙ. УЧЕНИЕ О ПРЕДЕЛАХ. Глава первая. Основные свойства пределов. Глава первая. Основные свойства пределов. 307. Определения. Возьмем сумму членов бесконечной убывающей Г. П.: l + 1/2 + 1/4 + 1/8 + ... (знам. 1/2). Сумма эта при неограниченном увеличении числа членов увеличивается, приближаясь (ч. I, отдел 10 глава 3 § 252) к постоянному числу 2 так, что разность 2 — (l + 1/2 + 1/4 + 1/8 + ... ) при достаточном увеличении числа слагаемых делается меньше любого данного положительного числа (напр., меньше 0,000001) и при дальнейшем увеличении числа слагаемых остается всегда меньше этого числа. При этих условиях мы говорим, что 2 есть предел суммы l + 1/2 + 1/4 + 1/8 + ... если число слагаемых в ней увеличивается неограниченно. В этом примере переменное число (сумма членов прогрессии), приближаясь к своему пределу, остается меньше его. Но могут быть случаи, когда переменное число, приближаясь к своему пределу, остается больше его. Напр., если предположим, что в сумме 1 + 1/х буква х означает переменное положительное число, неограниченно увеличивающееся, то сумма эта будет приближаться к пределу 1, оставаясь всегда больше 1. Может даже случиться, что переменное число так изменяется, что оно делается то больше, то меньше своего предела. Такой случай мы уже видели, когда говорили о пределе суммы членов бесконечно убывающей Г. П. (ч. I, отдел 10 глава 3 § 253): 2, — l , + 1/2 , — 1/4 , + 1/8 , ... )(знам.—1/2). Предел этот равен 1 1/3, и суммы двух, трех, четырех и т. д. членов прогрессии переходят через значения: 2 — 1 = 1 < 1 1/3; 2 — l + 1/2 =11/2 >1 1/3; 2, — l + 1/2 — 1/4 = 1 1/4 < 1 1/3; которые попеременно то больше, то меньше своего предела. После этих примеров будет понятно следующее определение предела: если переменное число х при своем изменении приближается к постоянному числу а таким образом, что абсолютная величина разности а — х делается и при дальнейшем процессе изменения х всегда остается меньше любого данного положительного числа (как бы мало оно ни было), то это постоянное число а называется пределом переменного х. Вместо того чтобы говорить: „число х имеет предел а", часто говорят короче: „х стремится к а" и письменно выражают это так: х —> а. Если абсолютная величина переменного числа увеличивается неограниченно (беспредельно), то условно говорят, что оно стремится к + ∞ или к — ∞ (смотря по его знаку), если же абсолютная величина переменного числа делается и остается меньшей любого данного положительного числа, то говорят, что оно стремится к нулю. Переменное число, стремящееся к ∞, называется часто бесконечно большим, а переменное число, стремящееся к нулю, называется бесконечно малым. Должно однако помнить, что эти названия не означают „число очень большое", или „число очень малое"; они характеризуют не самое число, а процесс его изменения: число, называемое „бесконечно большим", изменяется так, что оно делается и остается (по абсолютной величине) больше любого данного числа, а число, называемое „бесконечно малым", изменяется так, что оно делается и остается (по абсолютной величине) меньше любого данного положительного числа. Если воспользоваться в этом смысле названием „бесконечно малое число", то определение предела можно высказать короче так: Постоянное число а называется пределом переменною числа х, если разность х — а есть бесконечно малое число. Встречается еще название „конечное число". Так называется всякое число, которое не стремится к ± ∞. Постоянное число тоже может быть названо конечным. 308. Некоторые свойства бесконечно малых чисел. 1) Алгебраическая сумма бесконечно малых чисел бесконечно мала (если число слагаемых не увеличивается беспредельно). Возьмем, напр., три бесконечно малых числа α , β и γ (они могут быть положительные и отрицательные). Чтобы показать, что сумма их α + β + γ бесконечно мала, надо убедиться, что абсолютная величина этой суммы делается и остается меньше всякого данного положительного числа, напр., меньше 1 миллионной. Действительно, так как числа α , β и γ бесконечно малы, то это значит, что при своем изменении абсолютная величина каждого из них делается и остается меньше любого данного числа, в том числе и меньше 1/3 миллионной; значит, тогда абсолютная величина суммы α + β + γ делается и остается меньше 1/3 + 1/3 + 1/3 т. е. меньше 1 миллионной. Заметим, что если одновременно с уменьшением слагаемых число их будет возрастать, то сумма их может оказаться и не бесконечно малой. Возьмем, напр., такие суммы: 1/10 + 1/10 + 1/10 +...+1/10 (10 слагаемых); 1/100 + 1/100 + 1/100 + ... + 1/100 (100 слагаемых); ................................................................................... Вообще 1/n + 1/n + 1/n + ... + 1/n (n слагаемых). Несмотря на то, что с увеличением знаменателя слагаемые уменьшаются неограниченно, сумма их остается неизменной (она равна 1). Возьмем еще такие суммы: 1/10 + 1/10 + 1/10 +...+1/10 (102 слагаемых); 1/100 + 1/100 + 1/100 + ... + 1/100 (1002 слагаемых); ................................................................................... Вообще 1/10 • + 1/n + 1/n + ... + 1/n (n2 слагаемых). Суммы эти вырастают неограниченно: первая равна 1/10 • 100 =10, 2) Произведение бесконечно малого числа на постоянное число бесконечно мало. Напр., произведение 100 α , в котором α какое-нибудь бесконечно малое число, делается и остается (по абсолютной величине) меньшим любого данного положительного числа, напр., меньшим 1 миллионной, так как α делается и остается меньшим всякого данного положительного числа, в том числе меньшим и 1/100 миллионной. 3) Произведение бесконечно малого числа на другое бесконечно малое число бесконечно мало. Если произведение бесконечно малого числа на постоянное число способно сделаться так малым, как угодно, то произведение бесконечно малого числа на другое бесконечно малое число и подавно может сделаться как угодно малым (с уменьшением множителя произведение уменьшается). 4) Частное от деления бесконечно малого числа на постоянное число бесконечно мало. Напр., частное α : 1/10 бесконечно мало, так как оно равно произведению α • 10, т. е. произведению бесконечно малого числа на постоянное число. Замечание. Частное от деления бесконечно малого числа на другое бесконечно малое число может иногда равняться постоянному числу, иногда бесконечно малому и иногда бесконечно большому; все зависит от того, по какому закону уменьшается делимое и по какому закону уменьшается делитель. Возьмем, напр., такие три частные:
Положим, что α есть бесконечное малое число. Тогда первое частное, всегда равное 2, есть число постоянное; второе частное, равное α, есть число бесконечно малое и третье частное, равное дроби 1/α есть число бесконечно большое, так как дробь, у которой числитель постоянное число, а знаменатель неограниченно уменьшается, увеличивается беспредельно (ч. 1,отдел 4 глава 2 § 130). 309. Некоторые свойства пределов. 1) Переменное число, изменяющееся по определенному закону, не может иметь более одного предела. Предположим противное, а именно, что переменное число х, изменяясь по некоторому определенному закону, стремится к двум различным пределам, напр., к 5 и 5,1. Тогда, согласно определению предела, разности х — 5 и х — 5,1 должны быть бесконечно малые числа (положительные или отрицательные). Пусть х — 5 = α и х — 5,1 = β; Но это равенство невозможно, так как разность α — β, представляющая собою алгебраическую сумму α + (— β ) бесконечно малых чисел, бесконечно мала и, следовательно, она не может равняться постоянному числу. Значит, нельзя допустить, чтобы число х имело два различных предела. 2) Если разность двух переменных чисел (х и у) бесконечно мала (или равна нулю) и одно из них имеет предел, то и другое имеет тот же предел. Допустим, напр., что число х имеет предел 2. Тогда можно положить, что х = 2 + α, где α бесконечно малое число (положительное или отрицательное). Допустим, кроме того, что разность х — у равна бесконечно малому числу β (или нули,). Тогда: (2 + α) — у = β, откуда 2 — у = β — α. Так как разность β — α есть число бесконечно малое, то из последнего равенства видно, что 2 есть предел числа у. 3) (Обратная истина). Если два переменных числа (х и у) имеют общий предел, то их разность бесконечно мала (или равна 0). Положим, напр., что числа х и у оба имеют один предел 10. Следовательно, х — у = (10 + α) — (10 + β) = α — β. Так как разность α — β бесконечно мала или равна нулю, то и левая часть равенства, т. е. разность х — у, бесконечно мала или равна 0. 4) Предел алгебраической суммы переменных чисел равен алгебраической сумме пределов этих чисел (если число слагаемых ие бесконечно велико). Положим, мы имеем сумму трех переменных чисел: х + у + z, и пусть х —> 3, у —> 2 и z —> — 5. Тогда можно написать равенства: x = 3 + α; у = 2 + β ; z = — 5 + γ, где α, β и γ бесконечно малые числа. Следовательно, х + у + z = (3 + α) + (2 + β ) + (— 5 + γ) = (3 + 2 — 5) + (α+ β + γ). Откуда: (х + у + z) — (3 + 2 —5) = α+ β + γ. Правая часть этого равенства есть сумма бесконечно малых слагаемых, а потому она сама бесконечна мала; а из этого надо заключить, что переменная сумма х + у + z стремится к пределу 3 + 2 —5, т. е. к алгебраической сумме пределов. Это рассуждение можно повторить о четырех, пяти и более слагаемых, лишь бы число их не возрастало беспредельно (в противном случае сумма α+ β + γ + ... могла бы и не оказаться бесконечно малым числом). 5)Предел произведения переменных чисел равен произведению пределов этих чисел. Пусть имеем произведение ху двух переменных чисел, из которых первое стремится, положим, к пределу 2, а второе к пределу 3. Тогда: x = 2 + α и у = 3 + β и следовательно, ху = (2 + α)(3 + β ) = 2•3 + 3α + 2β + αβ; откуда: ху — 2•3 = 3α + 2β + αβ. Произведения 3α , 2β и αβ бесконечно малые числа; поэтому и сумма их бесконечно мала; а это означает, что ху —> 2•3, т. е. ху = (пред. x)•(пред. у). Этот вывод можно обобщить на произведение трех, четырех и более сомножителей. Так, рассматривая произведение хуz, как произведение только двух сомножителей ху и z , мы можем написать: пред. (хуz) = (пред, ху)•(пред. z) = (пред. x)•(пред. у)•(пред. z). 6) Предел частного от деления переменных чисел равен частному от деления пределов этих чисел, если только предел делителя не равен нулю. Пусть х —> 2 и у —> 3; тогда x = 2 + α и у = 3 + β , где α и β бесконечно малые числа. Следовательно,
В дроби, стоящей в правой части этого равенства, числитель бесконечно малое число, так как он есть алгебраическая сумма двух бесконечно малых чисел; знаменатель же, имея пределом число 32, не равное нулю, не может стремиться к нулю. Если же числитель дроби бесконечно мал, а знаменатель не бесконечно мал, то такая дробь бесконечна мала. Значит, из написанного выше равенства мы должны заключить, что
7) Предел степени, в которой основание есть переменное число, а показатель постоянное, равен той же степени предела основания. Ограничимся случаем, когда показатель степени есть число целое положительное. В этом случае теорема эта представляет собою простое следствие теоремы о пределе произведения. Так: пред. (x3) = пред. (ххх) — (пред. х) (пред. х) (пред. х) = (пред. х)3. Добавим еще без доказательства, как допущения, следующие две истины о пределах: 8) Если переменное число все возрастает, оставаясь однако меньше какою-нибудь постоянною числа, то оно имеет предел. Возьмем, напр., приближенные значения √2, взятые с недостатком и вычисленные с точностью сначала до 1, потом до 1/10, затем до 1/100 и т. д. Мы получим тогда бесконечный ряд чисел: 1; 1,4; 1,41; 1,414; 1,4142; 1,41421; и т. д. Числа эти, по мере удаления от начала ряда, все увеличиваются, но остаются всегда меньше некоторого постоянного числа, напр., меньше 1,5; при этих условиях мы должны допустить, что взятый нами ряд, по мере его продолжения, стремится к какому-то определенному пределу (этот предел есть иррациональное число√2). 9) Если переменное число все убывает, оставаясь однако больше какою-нибудь постоянного числа, то оно имеет предел. Возьмем для примера ряд приближенных значений √2 взятых с избытком, с точностью до1 до 1/10, до 1/100 и т. д: 2; 1,5; 1,42; 1,415; 1,4143; 1,41422; и т. д. По мере удаления от начала ряда числа эти все уменьшаются, но остаются постоянно больше 1,4; при этих условиях мы должны допустить, что ряд стремится к пределу (он равен иррациональному числу √2). Применение учения о пределах к вопросам элементарной геометрии. 310. Длина окружности. Предварительно докажем следующие три вспомогательные истины (леммы): 1) При неограниченном увеличении числа сторон правильного многоугольника, вписанного в данную окружность, длина его стороны стремится к нулю. Пусть р есть периметр какого-нибудь правильного многоугольника, вписанного в окружность, и n число его сторон. Тогда длина одной стороны этого многоугольника выразится дробью p/n Положим, что число сторон n неограниченно возрастает при том же радиусе окружности. Тогда в этой дроби знаменатель будет неограниченно возрастать, тогда как числитель не может возрастать беспредельно, так как он постоянно остается меньше периметра любого описанного многоугольника (напр., описанного квадрата; в геометрии доказывается, что периметр выпуклoго объемлемого многоугольника меньше периметра объемлющего многоугольника.). Вследствие этого дробь p/n , выражающая длину одной стороны многоугольника, должна стремиться к 0. 2) Разность между радиусом данной окружности и апофемою правильного многоугольника, вписанного в эту окружность, стремится к нулю, если число сторон многоугольника увеличивается неограниченно.
Поэтому разность ОА — ОС, будучи меньше АС, и подавно стремится к нулю. 3) Разность между периметрами одноименных правильных многоугольников одного описанного, другого вписанного в данную окружность стремится к нулю, когда число сторон в этих многоугольниках неограниченно увеличивается.
Поэтому, обозначив периметры многоугольников: вписанного p и описанного Р, можем написать пропорцию:
Из этой пропорции составим производную (ч. I, отдел 2, глава 7 § 98):
Вообразим теперь, что число сторон многоугольников неограниченно увеличивается. Тогда разность ОС1 — ОС будет стремиться к нулю, периметр р постоянно остается меньшим периметра любого описанного многоугольника, а знаменатель ОС увеличивается. Из этого следует, что дробь, стоящая в правой части последнего равенства, стремится к нулю; следовательно, и левая часть равенства, т. е. Р—р, стремится к нулю. 311. Основная теорема. Теперь мы можем установить следующую теорему, на которой основано определение длины окружности. Периметр правильного многоугольника, вписанною в данную окружность, при неограниченном удвоении числа сторон этого многоугольника стремится к пределу; предел этот не зависит от того, с какого многоугольника мы начали удвоение. Положим, мы начали удвоение с правильного треугольника, беря 6-угольник, потом 12-угольник, 24-угольник и т. д. без конца. Обозначим через р переменный периметр многоугольника, изменяющегося по этому закону удвоения. Вообразим еще, что строя правильные вписанные многоугольники, мы каждый раз строим и соответственные правильные описанные многоугольники, т. е., напр., построив правильный 6-угольник вписанный, мы строим также правильный 6-угольник описанный, и т. д. Обозначим через Р переменный периметр изменяющегося описанного многоугольника.
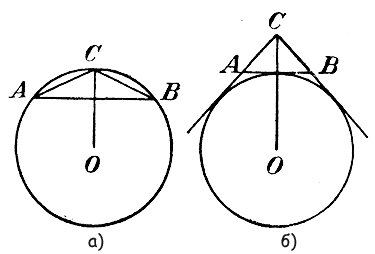
Так как при каждом удвоении числа сторон вписанного многоугольника мы вместо прямой АВ (черт. а) ) берем ломаную АСВ, а при каждом удвоении числа сторон описанного многоугольника мы вместо ломаной АСВ (черт. б) ) берем прямую АВ, то при неограниченном удвоении числа сторон переметр р увеличивается, а периметр Р уменьшается, причем первый, увеличиваясь, остается однако меньше периметра любого описанного многоугольника, а второй, уменьшаясь, остается больше периметра любого вписанного многоугольника. Из этого следует, что (согласно допущению 8-у § 309) р имеет предел, также (согласно допущению 9-у того же §) и Р имеет предел. Пределы эти должны быть одинаковы (§ 309,2), так как разность Р—р, по доказанному, стремится к нулю. Остается доказать, что этот общий предел не зависит от того, с какого многоугольника мы начали удвоение. Пусть Р и р будут переменные периметры описанного и вписанного многоугольников, получаемые удвоением числа сторон какого-нибудь одного начального многоугольника (напр, треугольника), а Р1, и p1 переменные периметры описанного и вписанного многоугольников, получаемыe удвоением числа сторон какого-нибудь другого начального многоугольника (напр, квадрата). Пусть Т есть общий предел для Р и р и T1 общий предел для Р1, и p1 Надо доказать, что T=T1. Примем во внимание, что при неограниченном удвоении числа сторон обе разности Р— р и Р1— p1 по доказанному, стремятся к нулю; следовательно, и сумма этих разностей стремится к нулю. Эту сумму можно представить так: (Р— р) + (Р1— p1) = (Р— p1) + (Р1— р ) —>0. Так как Р > p1 и Р1 > р, то обе разности, стоящие в скобках, положительные числа. Если же сумма положительных чисел стремится к нулю, то каждое слагаемое и подавно, будучи меньше суммы, стремится к нулю. Итак: (Р— p1) —>0; (Р1— р ) —>0. Поэтому (§ 309, 2) пред. Р = пред. p1 и пред.Р1= пред. р, т. е. T=T1. Теперь мы можем высказать следующее определение: общий предел, к которому, при неограниченном удвоении числа сторон, стремятся периметры правильных многоугольников как вписанных в окружность, так и описанных около нее, принимается за длину этой окружности. 312. Отношение длины окружности к ее диаметру. Пусть имеем две окружности с радиусами R и R1 Впишем в ту и в другую окружность какие-нибудь одноименные многоугольники. Пусть их периметры будут р и p1 Тогда, вследствие их подобия: р : p1 = R : R1. Обозначим длины этих окружностей через С и C1 и положим, что (С— α) : (C1 — α1) = R : R1 Пусть все величины, входящие в эту пропорцию, выражены числами. Тогда пропорция становится числовою, и мы можем из нее вывести: (С— α)R1 = (C1 — α1)R, т. е. СR1— αR1 = C1R— α1R откуда: СR1— C1R = αR1— α1R Вообразим теперь, что число сторон вписанных многоугольников неограниченно удваивается. Тогда переменные периметры р и p1 будут стремиться к своим пределам С и C1 и потому числа α и α1 будут стремиться к нулю; равенство же, выведенное нами сейчас, сохраняется при всяких значениях чисел α и α1. Левая часть этого равенства есть разность постоянных чисел; такая разность равна или нулю, или какому-нибудь другому постоянному числу. Значит, и правая часть равенства должна быть равна или нулю, или другому постоянному числу. Но разность переменных чисел, из которых каждое стремится к нулю, не может равняться никакому постоянному числу, отличному от нуля; значит, необходимо, чтобы эта разность равнялась нулю. Тогда и СR1— C1R = 0, откуда: С : C1 = R : R1. (ч. I,отдел 2 глава 7 § 94.) Умножив оба члена второго отношения на 2, мы не изменим этого отношения, следовательно, С : C1 = 2R : 2R1, откуда: C : 2R = C1 : 2R1 т. е. отношение длины окружности к ее диаметру есть число постоянное для всех окружностей. Число это, обозначаемое греческою буквою π, равно 3,1415... Из равенства C : 2R = π выводим: C=2πR. 313. Площадь круга. Пусть Р, р и а будут площадь, периметр и апофема какого-нибудь правильного многоугольника, вписанного в круг радиуса R. Тогда, как известно, Р = 1/2 ра Если станем неограниченно удваивать число сторон этого многоугольника, то величины Р, р и а сделаются переменными, причем р стремится к пределу, называемому длиною С окружности, а а стремится к R. Так как предел произведения равен произведению пределов, то пред.Р = пред.1/2 р • пред.а Этот предел принимается за меру площади круга. Подставив вместо С произведение 2πR, найдем: площадь круга = πR2. 314. Боковая поверхность цилиндра и конуса. Пусть р и а будут периметр и апофема правильного многоугольника, вписанного в окружность основания цилиндра или конуса, Н — высота цилиндра и L — образующая конуса. Впишем в цилиндр призму и в конус пирамиду, приняв за их основания правильные многоугольники, вписанные в окружность основания. Тогда: бок. пов. призмы = рН; бок. пов. пирамиды = 1/2 рl, где l есть апофема вписанной пирамиды. Вообразим теперь, что число сторон вписанного многоугольника (следовательно, и число боковых сторон призмы и пирамиды) неограниченно удваиваются. Тогда р стремится к С и l к L; следовательно: пред. бок, пов. призмы = СН; пред. бок, пов. пирамиды = 1/2 CL. Пределы эти принимаются за численные величины боковых поверхностей цилиндра и конуса. 315. Объем пирамиды.
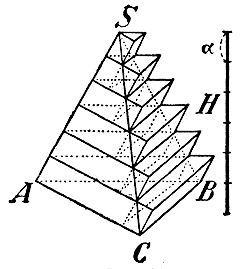
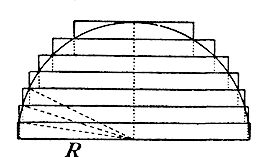
Беря каждый из этих треугольников за основание, построим, как видно из чертежа, ряд трехгранных призм, выходящих некоторою своею частью за пирамиду и имеющих высоту 1/n H = α . Всего таких призм, очевидно, окажется n. Сумма их объемов, конечно, больше объема пирамиды. Докажем, что при неограниченном увеличении n эта сумма стремится к пределу, равному объему V пирамиды. Для этого, беря каждый треугольник сечений за верхнее основание призмы, построим еще ряд призм, входящих внутрь пирамиды (на чертеже их боковые ребра изображены пунктирными линиями) и имеющих каждая высоту 1/n H = α. Таких призм окажется, очевидно, n — 1. Сумма их объемов менее объема пирамиды, так что величина объема пирамиды V заключена между суммой n — 1 объемов призм входящих и суммою n объемов призм выходящих. Поэтому, если мы докажем, что разность между этими двумя суммами стремится к нулю, когда число n делений высоты (следовательно, и число призм) неограниченно увеличивается, то- отсюда заключим, что V есть общий предел двух этих сумм. Сравнивая призмы выходящие с призмами входящими, замечаем, что первая сверху выходящая призма равна первой сверху входящей призме, вторая выходящая равна второй входящей, и т. д. до предпоследней (n — 1)-й выходящей, которая равна последней входящей. Поэтому разность между суммою объемов выходящих и суммою объемов входящих призм равна объему одной выходящей нижней призмы, т. е. равна произведению Рα (так как объем призмы равен произведению площади основания на высоту). При неограниченном увеличении числа делений n число α = Н : n стремится к нулю, а потому и произведение Рα стремится к нулю. Но так как разность между суммою объемов выходящих призм и объемом V пирамиды, очевидно, меньше разности между суммою объемов выходящих призм и суммою объемов входящих, то первая разность и подавно стремится к нулю; а это значит, что V есть предел суммы объемов выходящих призм (а также и входящих). Найдем теперь сумму всех объемов выходящих призм и затем предел этой суммы, который и будет служить чиоленною величиною объема пирамиды. Обозначим объемы выходящих призм, начиная с верхней, буквами v1 ,v2 ,v3 ,....vn , а площади их оснований буквами pvpit p1 , p2 , p3 ,..., pn-1 , pn= Р= пл. ABC. Тогда: v1 = p1α; v2 = p2α; v3 = p3α; ... vn = pnα; Следовательно, v1 + v2 + v3 +....+ vn= α( p1 + p2 + p3 +... + pn ) Но
Поэтому:
Добавим к этим равенствам еще одно:
Так как
то
(так как pn = Р и αn = Н). Дробный множитель, стоящий в этом выражении, может быть представлен так:
Отсюда видно, что предел этого множителя, когда n неограниченно увеличивается, равен 1/6 • 1• 2 = 2/6 = 1/3 Следовательно, V=пред. (v1 + v2 + v3 +....+ vn) = PH • 1/3 = 1/3 PH, т. е. объем пирамиды равен одной трети произведения площади основания на высоту. Теорему эту можно распространить на всякую многогранную пирамиду, так как такую пирамиду диагональными плоскостями можно разбить на несколько трехгранных пирамид. 316. Объемы цилиндра и конуса. Рассматривая эти объемы как пределы объемов правильных вписанных призм (для цилиндра) и пирамид (для конуса), мы найдем: Объем цилиндра = QH, ,, конуса= 1/3 QH, где Q есть площадь основания и Н высота. 317. Объем шара.
Приняв каждый круг сечений за нижнее основание цилиндра, построим n цилиндров, выходящих некоторою частью из шара, высотою каждой в 1/n R = α. Затем, приняв каждый круг сечений за верхнее основание цилиндра, построим еще ряд цилиндров, входящих внутрь шара, с высотою у каждого в 1/n R = α. Таких цилиндров будет n — 1. Обозначим объемы выходящих цилиндров, начиная снизу, буквами: v1 ,v2 ,v3 ,....vn. Тогда объемы входящих цилиндров будут, очевидно, начиная опять снизу: v2 ,v3 ,v4 ,....vn и разность между суммою выходящих цилиндров и суммою входящих равна одному объему v1 = πR2α. Если вообразим, что число делений n неограниченно увеличивается, то число α = 1/n R будет стремиться к 0. А так как объем полушария меньше суммы объемов выходящих цилиндров, но больше суммы объемов входящих, то разность между первою суммою и объемом полушария V, а также и разность между V и второю суммою, и подавно будет стремиться к нулю. Из этого заключаем, что объем V есть общий предел как суммы выходящих цилиндров, так и суммы входящих. Найдем теперь сумму объемов выходящих цилиндров. Обозначив радиусы оснований этих цилиндров, начиная с нижнего, буквами r1 = R; r2, r3,...rn, мы будем иметь: v1 + v2 + v3 +....+ vn = π α ( r12 + r22 + r32 + ...+ rn2 ) Из чертежа усматриваем: r12= R2; r22 = R2 — α2; r32 = R2 —(2 α)2; ..., rn2 = R2 — [(n -1)α]2. Следовательно:
и
Но
поэтому:
Найдем теперь предел этого выражения, если п—> ∞:
Следовательно,
Отсюда:
где D означает диаметр шара. Таким же путем можно найти объем сферического слоя и объем сфери ческого сегмента. 318. Поверхность шара. Эту поверхность можно найти как предел поверхности, производимой вращением правильной ломаной линии, вписанной в полуокружность, вокруг диаметра этой полуокружности. Но если предварительно найдена формула, выражающая объем шара, то величину поверхности шара можно найти весьма просто. Для этого можно воспользоваться таким простым рассуждением (не вполне, впрочем, строгим).
Объем каждой из этих пирамидок равен 1/3sR, если s означает поверхность участка и R радиус шара. При сложении объемов всех пирамидок можно вынести за скобки общим множителем 1/3R; тогда внутри скобок получится сумма всех участков, которая составит полную поверхность S шара. Значит, объем шара равен1/3RS. Но так как, с другой стороны, тот же объем шара равен 4/3 π R3мы можем написать уравнение: 1/3RS = 4/3 π R3 откуда: S = 4/3 π R3 : 1/3R = 4π R2 Так как π R2 выражает площадь большого круга шара, то можно сказать, что поверхность шара равна учетверенной площади большого круга.
|