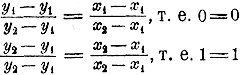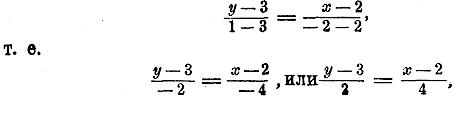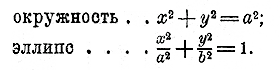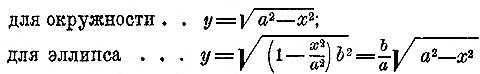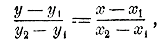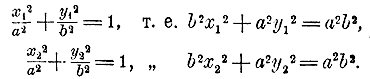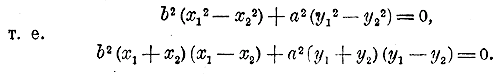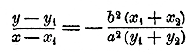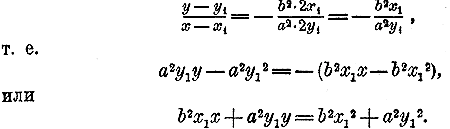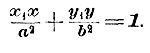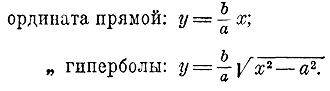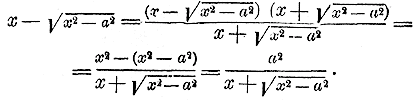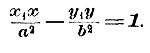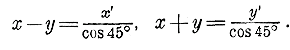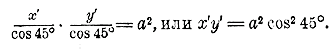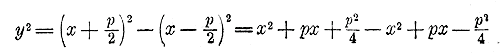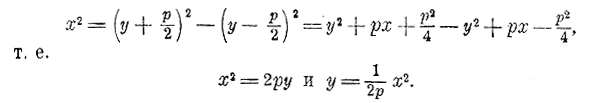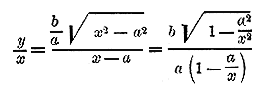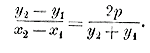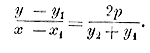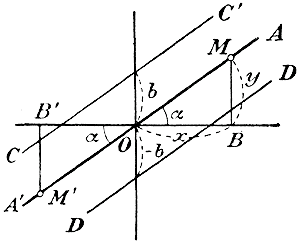
ОТДЕЛ ШЕСТНАДЦАТЫЙ.

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ.

Глава первая. Прямая линия.
Глава вторая. Окружность и эллипс.
Глава   третья. Гипербола.
Глава четвертая.Парабола.

Глава первая.

Прямая линия.

350. Уравнение прямой. Мы знаем (ч. I, отдел 3 глава 3 § 115), что уравнение 1-й степени с 2-мя неизвестными вида

у = ах + b

выражается помощью координатных осей в виде прямой линии, которая образует с положительным направлением оси x-ов угол α, определяемый равенством: tg α = а, и отсекает от оси у-ов отрезок, равный b. Так как к такому виду может быть приведено всякое уравнение 1-й степени с 2-мя неизвестными х и у, то такое уравнение выражается при помощи координатных осей в виде прямой линии (почему оно и называется линейным уравнением).

Покажем теперь, что, обратно,  всякая прямая линия может быть выражена уравнением 1-й степени с двумя  неизвестными х и у.

Сначала допустим, что прямая АА' (черт. 1) проходит через начало координат О, образуя с Ох острый угол α.

Черт.1

Возьмем на этой прямой произвольную точку М, абсцисса которой есть х = ОВ и ордината у = МВ. Из треугольника ОМВ видно, что y = x tg α, или у = ах, если tg α обозначим а. Выведенное нами уравнение у = ах верно не только для точек полупрямой ОА, но и для точек полупрямой ОА'. Возьмем, напр., точку M', которой координаты будут: x = — ОВ', у = — M'В'. Из тр-ка ОВ'М' находим: M'B' = B'O tg α, т. е. — y = — x tg α, или y = x tg α. Таким образом, уравнение у = ах верно для всякой точки прямой АА'.

Теперь допустим, что прямая АА' проходит через начало координат, но образует с Ох не острый угол, а тупой α (черт. 2).

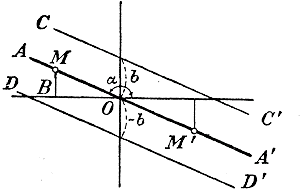
Черт.2

Если M есть какая-нибудь точка этой прямой, то ее абсцисса х = — ОВ и ордината у = MВ, и мы из тр-ка ОMВ находим:

MВ =ОВ tg MОВ,

т. е.

у = — x tg MОВ.

Но tg MOB = tg(180°—α) = — tg α; значит, у = — х( — tg α)= х tg α = ax, если попрежнему обозначим tg α через а. Подобное же уравнение получим и для любой точки M, расположенной на ОА'.

Наконец, допустим, что дана прямая СС' или DD' (черт. 1 и 2), не проходящая через О, а отсекающая от оси у-ов отрезок, равный b (или — b). Тогда, проведя через точку О вспомогательную прямую АА' || CC'(или || DD'), мы получим для этой щямой уравнение у = ах, где a = tg α. Но очевидно, что при одной и той же абсциссе х ординаты точек прямой СС' больше ординат точек прямой АА' на b, а прямой DD' меньше на b; значит, уравнение прямой СС' будет у = ах + b, а прямой DD' у = ах — b, где а есть попрежнему тангенс угла, образованного прямой с положительным направлением оси х-ов.

Частные случаи. 1) Если а = 0, т. е.   если данная прямая параллельна   оси х-ов,  то уравнение   будет:   у = b.   Если она при этом сливается с осью х-ов, то уравнение окажется:

у = 0.

2) Если данная прямая параллельна оси у-ов и отсекает от оси х-ов отрезок k, то уравнение такой прямой будет: х = к (ордината, как не входящая в уравнение, остается произвольной).

351.  Уравнение  прямой,  проходящей  через данную точку.

Если прямая у = ах + b проходит через точку (x₁ , y₁  ), то мы должны иметь равенство

y₁ = аx₁ + b

Вычтя почленно это равенство из уравнения  у = ах + b, получим:

у — y₁ = а(х — x₁).

Что прямая, определяемая этим уравнением, действительно проходит через точку (x₁ , y₁  ), видно из уравнения непосредственно: подставив вместо х  и у соответственноy₁ и x₁ получим тождество: 0 = 0.

Угловой коэффициент а остается неопределенным, так как через одну точку может проходить бесчисленное множество прямых.

Примеры. Уравнение прямой, проходящей через:

точку (2,3) будет: у — 3 = а(х — 2);
„ ( — 2,3)      „   у—3 = a(x + 2);
„ ( — 2,—3)   „  у + 3 = а(х + 2);
,, (0,3)            ,,   у — 3 = ах;          
,,        (0,0)     „  у = ах.                

352.  Уравнение прямой, проходящей через 2 данные точки.

Положим, что прямая:

у — y₁ = а(х — x₁),                                    (1)

проходящая через точку (x₁ , y₁ ), проходит еще через другую точку (x₂ , y₂ ). Тогда координаты этой другой точки должны удовлетворять уравнению прямой, и следовательно:

y₂ — y₁ = а (x₂ — x₁), откуда находим:

Мы  нашли   таким   образом  угловой   коэффициент  прямой, проходящей через 2 данные точки (x₁ , y₁ ) и (x₂ , y₂ ).

Теперь уравнение (1) можно написать так:

что можно изобразить в таком удобном для запоминания виде:

Что прямая, удовлетворяющая этому уравнению, проходит через точки (x₁ , y₁ ) и (x₂ , y₂ ), видно из уравнения непосредственно; подставив вместо х и у соответственно x₁ , y₁ или x₂ , y₂получим тождества:

Пример. Уравнение прямой, проходящей через точки A (2, 3) и B(— 2, 1), будет:

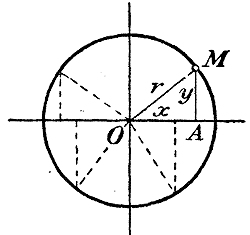
что после упрощения дает: х — 2у = — 4.

Глава вторая.

Окружность и эллипс.

353. Уравнение окружности.

Действительно, в каком бы угле мы ни взяли точку окружности, координаты ее всегда будут катетами пряумоугольного треугольника, у которого гипотенуза есть r; только катеты эти иногда приходится брать со знаком +, иногда  со  знаком—.   
Но  так как   ( + х)² = ( — х)²  и ( + y)² = ( — y)², то уравнение х²  + y²  = r ² останется в силе для любой точки окружности, и потому его можно назвать уравнением окружности, у которой центр совпадает с началом координат.

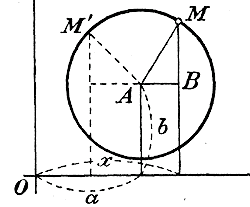
(а — х )² + (b — у )² = r ²

что тождественно уравнению, выведенному для точки M.

354.    Определение   эллипса.

Эллипсом называется геометрическое место точек на плоскости, сумма расстоянии которых от двух данных точек этой плоскости есть величина постоянная.

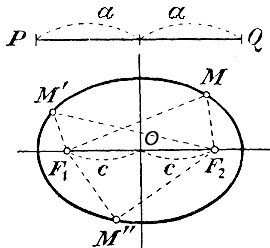
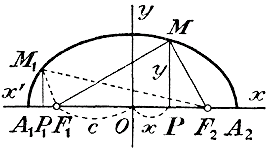
355. Построение эллипса непрерывным движением. Эллипс можно начертить непрерывным движением карандаша. Для этого возьмем нить, длина которой равна PQ (черт. 5) и укрепим ее концы в точках F₁ и F₂ . Затем, натянув нить острием карандаша, станем двигать карандашом по бумаге, наблюдая, чтобы нить вcегда была в натяжении. При движении карандаш опишет замкнутую кривую, вcе точки которой находятся на таких расстояниях от F₁ и F₂ ,что их сумма равна длине нити, т. е. отрезку PQ.

Длина данного отреза PQ обозначается обыкновенно 2а , а расстояние между точками F₁ и F₂ обозначается 2с. Точки эти называется фокусами, а прямые MF₁ и MF₂  соединяющие какую-нибудь точку M эллипса с фокусами, называется радиусами-векторами.

Точка О, означающая середину отрезка F₁F₂, называется центром эллипса. Всякая хорда эллипса, проходящая через центр, называется диаметром.

Из тр-ка F₁MF₂ видно, что MF₁ + MF₂ > F₁F₂ т. е. 2а > 2с и следовательно, а > с.

356. Построение эллипса по точкам (черт. 6).

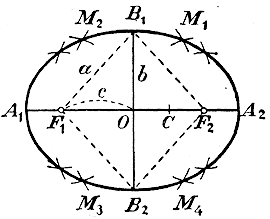
Эти точки тоже принадлежат эллипсу, так как B₁F₁+B₁F₂ = 2a и B₂F₁+B₂F₂ = 2a (прямая, проходящая через B₁ и B₂, перпендикулярна к А₁А₂ и делит А₁А₂ пополам в точке О).

Четыре точки А₁ , А₂ , B₁ и B₂ называются вершинами эллипса.
Отрезки прямых А₁А₂ и B₁B₂ называются осями эллипса, причем А₁А₂ есть большая ось, а B₁B₂ — малая оcь. Длина малой оcи обозначается 2b.

Из тр-ка F₁B₁O, в котором F₁B₁ = a, ОB₁ = b и F₁O = c, видно, что b² = a² — c².

Кроме четырех вершин можно построить сколько угодно других точек эллипса таким образом. Возьмем на отрезке F₁F₂ какую-нибудь точку С и, дав циркулю расстворение, равное А₁С, описываем этим расстворением 4 небольшие дуги: две из центра F₁, (одну выше прямой А₁А₂, другую ниже ее, обе направо от B₁B₂) и две из центра F₂ (одну выше А₁А₂ другую ниже, обе налево от B₁B₂). Затем дадим циркулю расстворение, равное СА₂, и этим расстворением описываем также 4 небольшие дуги: две из центра F₁ и две из центра F₂ . Если взятая точка С расположена между F₁ и F₂, то дуги, описанные из центра F₁пересекутся с дугами, описанными из центра F₂, так как расстояние между центрами F₁ и F₂ ( = 2с) меньше суммы радиусов дуг, которая равна А₁А₂ ( = 2а), но больше их разности ( = 2ОC) (Так как А₁C = а + OC и А₂C = a — OC. )

В пересечении получим четыре точки: M₁ , M₂ , M₃, M₄ принадлежащие эллипсу. Взяв вместо С другую точку между F₁ и F₂, мы подобным же построением получим еще 4 точки, и т. д. Когда, таким образом, получится довольно много точек, их все можно обвести непрерывней кривой, которая и будет эллипс.

Форма эллипса  зависит от величины отношения  ^c/_a,  называемого эксцентриситетом. Отношение это изменяется от 0 (когда с = 0) до 1 (когда с = а). Когда с = 0 и, значит, оба фокуса совпадают c центром, тогда эллипс обращается в окружность радиуса а, если же с = а, то фокус F₂ совпадает с А₁ и фокус F₂ с А₂; в этом случае эллипс обращается в отрезок А₁А₂ . Значит, чем ближе эксцентриситет к 0, тем более эллипс расширяется в вертикальном направлении, приближаясь к кругу, а чем ближе эксцентриситет к 1, тем более эллипс сжат в вертикальном направлении, приближаясь к прямой А₁А₂.

357. Уравнение эллипса.

MF₁² = МР² + F₁P² = у² + (с + x)²,
MF₂² = МР ²+ PF₂² = у² + (с — x)²,

и следовательно,

√у² + (с + x)²  + √у² + (с — x)²  = 2а.

Можно проверить, что это уравнение верно для всякой точки верхней половины эллипса. Возьмем, например, еще точку M₁ , расположенную так, что основание P₁  перпендикуляра M₁P₁ лежит налево от F₁ . Для этой точки находим:

M₁F₁² = M₁P₁² + P₁F₁² = M₁P₁² + (P₁O — F₁O)= у² + (—x —с )²,

M₁F₂² = M₁P₁² + P₁F₁² = M₁P₁² + (P₁O + F₁O)= у² + (—x +с )²

и следовательно,

√у² + (—x —с)²  + √у² + (— x + с )²  = 2а.

Так как (—x —с )² = (x + с )² и (—x +с )²  = (с — x)², то это уравнение тождественно с выведенным ранее для точки M.

Подобным же образом можно убедиться, что уравнение остается верным и тогда, когда основание перпендикуляра падает направо от F₂ или между F₁ и  О.

Если же уравнение остается верным для всех точек верхней половины эллипса, то оно должно быть верным и для всех точек нижней его половины, так как эти точки отличаются от соответственных точек верхней половины только тем, что ординаты нижних точек отрицательны, а верхних положительны; но это отличие не может повлиять на уравнение, так как в него входят только квадраты ординат.

Теперь упростим выведенное уравнение, освободив его, прежде всего, от радикалов. Перенеся второй радикал направо, возвысим обе части уравнения в квадрат:

у² + (с + x)² = 4а² — 4а √у² + (с — x)²   + у² + (с — x)²

Значит:

4а √у² + (с — x)² = 4а² + (с — x)² — (с + x)², т. e.

4а √у² + (с — x)² = 4а² — 4cx

или

а √у² + (с — x)² = а² — cx

Вторым возвышением в квадрат находим:

а²у² +  а²c² —2а²cx + а²x² = а⁴— 2а²cx + c²x²,

а²у² + а²x² — c²x²  = а⁴— а²c² 

а²у² + (а² — c²) x² = а²(а² — c²)

Но а² — c² = b²; поэтому уравнение будет:

а²у² + b²x² = а²b²

Разделив все члены на а²b², мы придадим уравнению эллипса такой удобный для запоминания вид:

Таково уравнение эллипса в том случае, когда его большая ось лежит на оси x-ов, а малая на оси у-ов.

Если центр эляипса лежит не в начале координат, а в какой-нибудь точке (m, n), причем большая ось параллельна оси x -ов, то (как не трудно убедиться) уравнение будет такое:

Если же большая ось параллельна оси y-ов, то в уравнениях надо  заменить х на у, и наоборот, т. е. тогда уравнения будут:

358. Следствия.

2) Построим (черт. 9) на большой оси эллипса, как на диаметре, окружность,

Черт.9

и сравним уравнение этой окружности c уравнением эллипса:

Из уравнений находим:

Таким образом, при одной и той же абсциссе х ордината эллипса короче ординаты круга в отношении b : а. Если, напр., b : а = ¹/₂, то, разделив ординаты круга пополам, мы получим точки эллипса (это дает нам другой способ построения эллипса по точкам).

359. Эллипс как проекция круга. Вообразим 2 плоскости, образующие некоторый двугранный угол α (на чертеже 10 мы изобразили сечение ABC этого угла плоскостью чертежа, перпендикулярною к ребру угла α).

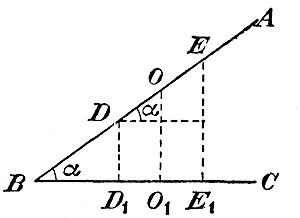
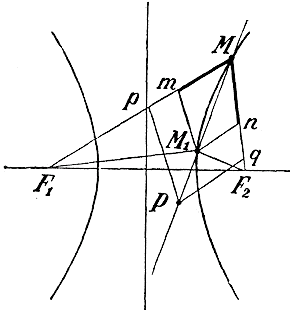
Черт.10

Пусть на плоскости АВ из тoчки О как центра описан круг, и DE есть его диаметр, перпендикулярный к ребру угла α . Зададимся вопросом, какова будет ортогональная (прямоугольная) проекция этого круга на плоскости ВС. Примем на плоскости АВ за ось x - ов диаметр круга, параллельный углу ребра α, а за ось у-ов — диаметр, ему перпендикулярный. Тогда абсциссы всех точек окружности проектируются на плоскости ВС в натуральную величину (так же, как и диаметр, параллельный ребру); ординаты же в проекциях окажутся меньше  в  одном и том же отношении, равном cos α (напр., проекция D₁E₁ диаметра DE будет DE cos α). Значит проекция окружности есть эллипс.

360. Свойство касательной. Возьмем на эллипсе две произвольные точки M и M₁, (черт. 11), проведем через них секущую и радиусы-векторы к каждой из них.

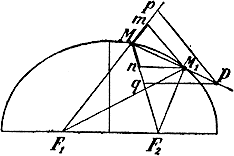
Возьмем еще на секущей произвольную точку Р и проведем Рр || M₁m и Pq || M₁n. Заметив, что четыреугольники РрMq и M₁mMn подобны (они состоят из подобных и сходственно расположенных треугольников), мы находим, что Мр = Mq. Теперь вообразим, что точка M₁ неограниченно приближается к М. Посмотрим, как будет изменяться тогда положение начерченных нами прямых. Секущая МР будет все более и более приближаться к некоторому предельному положению, именно к касательной к эллипсу в точке M; прямые M₁m и M₁n, уменьшаясь по длине, будут все более и более приближаться к перпендикулярности к радиусам-векторам F₁M и F₂M, так как углы F₁ и F₂ при вершинах равнобедренных треугольников F₁M₁m и F₂M₁n стремятся к 0° и, следовательно, каждый из углов при основаниях M₁m и M₁n этих треугольников стремится к 90°. Прямые Pq и Рр, будучи параллельными прямым M₁n и M₁m, стремятся тоже к перпендикулярности к F₂M к F₁M. В то же время отрезки Pq и Рр остаются всегда равными между собою.

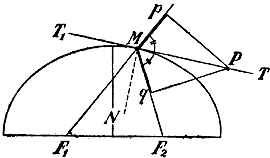
Из этого свойства касательной видно, что прямая MN (черт. 12), перпендикулярная к касательной в точке касания (такая прямая называется нормалью к кривой в точке касания), делит пополам угол F₁MF₂, образованный радиусами-векторами, проведенными из точки касания.

Действительно, так как /  рМТ=  /  T₁MF₁ (вертикальные) и /  рМТ= /  TMF₂ (по доказанному), то углы T₁MF₁ и TMF₂ равны; но тогда и дополнения их до 90°, т. е. углы F₁MN и NMF₂, также равны. Поэтому если в одном из фокусов поместим звучащее (или светящееся) тело, то лучи (звука или света), отразившись от вогнутой стороны эллипса (по закону: угол падения равен углу отражения), соберутся в другом фокусе (этим объясняются известные акустические свойства эллипсоидальных помещений).

361. Уравнение касательной.

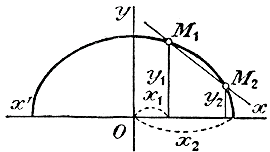
Так как точки M₁ и M₂  лежат на эллипсе, то координаты их  удовлетворяют уравнению эллипса:

Вычтя из первого уравнения второе, получим:

Отсюда находим:

Теперь уравнение секущей будет:

Вообразим теперь, что точка M₂ приближается все более и более к M₁  и, наконец сливается с M₁ . Тогда секущая обратится в касательную к эллипсу в точке M₁, а уравнение секущей сделается уравнением касательной Значит, уравнение касательной получится, если в уравнении секущей положим   х₂ = x₁   и  y₂ = y₁ :

Правая часть этого уравнения равна 1 (согласно уравнению эллипса); значит:

b²x₁x + a²y₁y = 1.

Таково уравнение касательной, проведенной через точку эллипса, имеющую координаты x₁ и x₂ Этому уравнению удобнее придать другой вид, разделив все его члены на a²b²

Глава   третья.

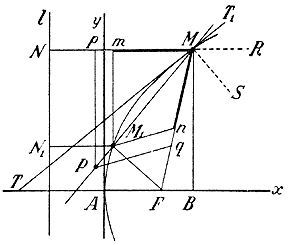
Гипербола.

362. Определение и построение. Мы уже раньше  встречались  с кривой,  называемой гиперболой,  а  именно  тогда, когда говорили о графике функции: у = ¹/_x  (отдел 15 глава7 § 348). Теперь мы рассмотрим эту кривую в более общем виде и прежде всего определим ее, как геометрическое место таких точек на плоскости, разность расстояний которых от двух данных точек этой плоскости есть величина постоянная.

Как и для эллипса, две точки (F₁  и F₂  черт. 14), от которых считаются расстояния, называются фокусами, а прямые, соединяющие эти точки о точками гиперболы, называются радиусами-векторами. Данная разность (PQ) двух радиусов-векторов, исходящих из какой-нибудь точки гиперболы, обозначается 2а, а расстояние между фокусами 2с.

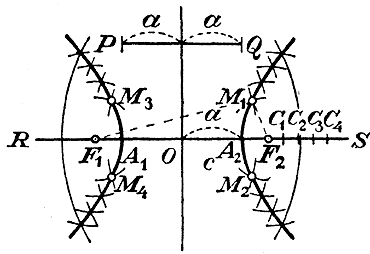
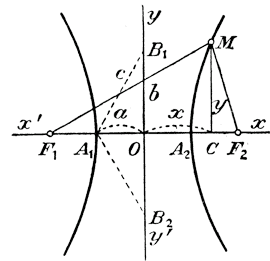
Черт.14

Для возможности существования гиперболы необходимо, чтобы а было меньше с, так как если  M₁  есть одна из точек гиперболы, то из треугольника F₁M₁F₂ видно, что
F₁M₁ — M₁F₂ < F₁F₂,   т. e. 2a < 2c и потому  a < c.

Гиперболу всего удобнее строить по точкам таким образом. Пусть фокусы F₁  и F₂  расположены на прямой RS. Разделим расстояние F₁F₂ пополам в точке О (она называется центром гиперболы) и отложим ОA₁ = ОA₂  = а. Полученные точки A₁ и A₂  принадлежат гиперболе, так как F₁A₁ = F₂A₂ и потому A₁F₂ — A₁F₁ = A₁F₂ — A₂F₂ = A₁A₂ = 2а; подобно этому и A₂F₁ — A₂F₂ = 2a. Эти две точки называются вершинами, а отрезок  A₁A₂ = 2a называется осью гиперболы. Возьмем теперь на продолжении F₁F₂ какую-нибудь точку C₁, (направо от F₂, или налево от F₁ все равно). Дадим циркулю расстворение, равное A₁C₁ и этим расстворением опишем две дуги: одну из центра F₁ и другую из центра F₂ . Затем, дав циркулю расстворение, равное A₂C₁ из центра F₂ засечем первую дугу в точках M₁   и M₂  , из центра F₁ засечем вторую дугу в точках M₃   и M₄. Полученные четыре точки принадлежат гиперболе, так как для каждой из них разность радиусов-векторов равна A₁A₂ = 2a. Беря затем другие произвольные точки C₂, C₃... (на продолжение F₁F₂, мы таким же путем построим для каждой из них 4 новых точки. Когда таких точек наберется достаточно много, мы можем обвести непрерывною кривою все те, которые лежат в правой половине чертежа, и все те, которые лежать в левой, тогда получим 2 ветви одной и той же кривой — гиперболы.

Большая или меньшая изогнутость гиперболы зависит от величины отношения  ^c/_a, которое (как и для эллипса) называется эксцентриситетом.

363. Уравнение гиперболы. Предположим; что ось A₁A₂ гиперболы лежит на оси x-ов и центр О совпадает с началом координат (черт. 15).

Черт.15

Пусть М будет произвольная точка гиперболы,имеющая координаты: х = ОС и y =MС. Из треугольников F₁MC и F₂МС находим:

MF₁² = МС² + F₁С²  =  y² + (с + х)²

MF₂² = МС² + F₂С² =  y²+(с — х)².

Следовательно,

√ y² + (с + х)² — √ y² + (с — х)² = 2a

Так же, как это мы делали для эллипса (§ 357), можно проверить, что это

уравнение верно для всякой точки гиперболы, как взятой на правой ветви, так и на левой, и расположенной как выше оси x-ов, так и ниже ее (предоставляем самим читателям сделать такую проверку).

 Упростим теперь выведенное уравнение совершенно так же, как мы это делали с уравнением эллипса, а именно: перенеся второй радикал в правую часть, возвысим обе части уравнения в квадрат:

 y² + (с + х)² = 4а² + 4а √ y² + (с — х)² + y² + (с — х)²,

значит:

— 4а √ y² + (с — х)² = 4а² + (с — х)² — (с + х)²  

т  е.

— а √ y² + (с — х)² = а² —  сх.

После вторичного возвышения в квадрат получим:

а² y² + а²с² — 2а²сх + а²х² = а⁴ — 2а²сх + c²х²,

а² y² + (а² — c²) х² = а⁴ — а²c² = а² (а² — c²).

В гиперболе а² < c²; поэтому мы можем положить: c² — а² = b² и,
следовательно, а²— c² = — b²; тогда уравнение будет:

а² y² — b²х²= — а²b² ,

или

b²х² — а² y² = а²b².

Наконец, разделив все члены на а²b², получим:

Заметим, что величина b, равная √c² — а², есть катет прямоугольного треугольника, у которого гипотенуза равна с, другой катет есть а. Построив на чертеже такой треугольник О иотложив еще OB₂=OB₁ мы получим 2 точки B₁ и B₂, которые называются мнимыми вершинами гиперболы; отрезок B₁B₂ равный 2b, называется мнимою (или побочною) осью гиперболы. В отличие от нее ось A₁A₂ = 2а называется вещественной (или главною) осью.

Если центр гиперболы лежит не в начале координат, а в какой-нибудь точке (m, n,) и главная ось параллельна оси х-oв, то уравнение гиперболы будет:

Еcли же главная ось параллельна оси у-ов, то в уравнениях надо x заменить на у и наоборот.

364. Следствия. 1) Так же, как и для эллипса (§ 358), из уравнения гиперболы можно вывести, что эта кривая имеет две оси симметрии, совпадающие с осями координат, и центр симметрии,  лежащий в начале координат.

2) Из уравнения гиперболы находим:

и, следовательно,

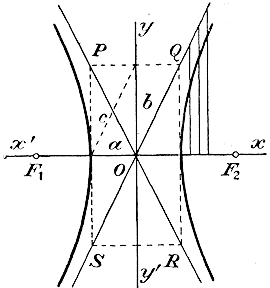
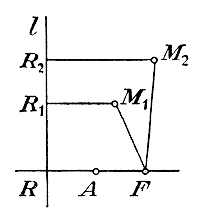
Из этой формулы видно, что гипербола не имеет точек, для которых абсолютная величина абсциссы х была бы меньше а, Наименьшая абсолютная величина х есть а ,
тогда у = 0 и х = ± а, т. е. тогда получаются вершины гиперболы A₁(— а,0) и A₂(а,0).

3) Из этой же формулы видно, что при неограниченном возрастании абсолютной величины х возрастает  неограниченно и абсолютная величина у. Значит, на гипербoле существуют точки, для которых и абсцисса и ордината как угодно велики; другими словами, обе ветви гиперболы бесконечно удаляются и от оси у-ов и от оси x-ов.

365. Асимптоты. На чертеже 16-м, на котором изображена гипербола о осями а и b, построим две прямые:

у = ^b/_a х и   y = —^b/_a х.

Так как x² — а²< x², то √x² — а² < x; поэтому при одном и том же значении х ордината гиперболы меньше ординаты прямой. Определим разность между ними:

^b/_a х — ^b/_a√x² — а² =  ^b/_a (х — √x² — а² )

При изменении х это выражение изменяется в том же смысле, в каком изменяется разнсть, стоящая внутри скобок (так как множимое — есть число постоянное и положительное). Но в этой разности при возрастании х возрастают одновременно и уменьшаемое х и вычитаемое √x² — а², и мы остаемся в неизвестности, как изменяется сама разность. Поэтому мы преобразуем ее таким образом:

Следовательно,

Теперь видно, что при неограниченном возрастаний х знаменатель полученной дроби возрастает неограниченно, тогда как числитель остается неизменным; значит, дробь при этом стремится к нулю. Таким образом, разность между ординатою прямой и ординатою гиперболы (при одном и том же значении х) стремится к нулю, когда абсцисса х неограниченно возрастает; другими словами, ветвь гиперболы по мере возрастания х все более и более приближается к проведенной нами прямой, однако никогда ее не достигает, так как ни при каком значении х (как бы велико оно ни было) разность между ординатами не делается равной нулю.

Сказанное об ординатах, расположенных в угле хОу, может быть повторено и об ординатах, лежащих в других углах. Значит,   можем  сказать,   что  прямые;  у = ^b/_a х и   y = —^b/_a х служат асимптотами гиперболы.

366. Свойство касательной. Касательная к гиперболе есть биссектриса угла, образованного радиусами-векторами, проведенными в точку касания.

Доказательство такое же, какое было изложено нами для эллипса (§ 360). На чертеже 17 сделано  соответствующее построение, причем буквы поставлены те же, что и на черт. 11.

Черт.17

Читатели могут сами проследить все доказательство, прочитывая то, что было изложено для эллипса. Отрезки Mm и Мn равны, так как они показывают, насколько радиусы-векторы увеличились при переходе от точки M к точке  M₁ , а эти увеличения должны быть равны, так как разность радиусов-векторов для всех точек гиперболы одна и та же.

Указанное свойстко касательной дает простой способ ее построения, когда точки касания и фокусы заданы.

367. Уравнение касательной. Уравнение секущей и затем уравнение касательной выводится для гиперболы совершенно так же, как это мы делали для эллипса (§ 361); разница только та, что координаты двух точек, через которые проведена секущая, приходится подставлять не в уравнение эллипса, а в уравнение гиперболы, а это уравнение отличается от уравнения эллипса:

эллипс:     гипербола:

только тем, что для гиперболы вместо b² берется — b². Поэтому и уравнение касательной к гиперболе должно отличаться от уравнения касательной к эллипсу только тем, что вместо b² надо подставить — b². Тогда уравнения касательных будут:

для эллипса      для гиперболы    

368. Равносторонняя   гипербола.  Если в уравнении  гиперболы положим а = b, то оно будет:

или    x² — y² = a²

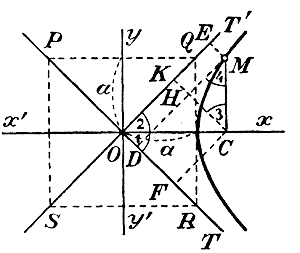
Такая гипербола  называется  равносторонней;  она  представляет ообою такой же частный случай по отношению к гиперболе, какой окружнооть (x² + y² = r²) представляет по отношению к эллипсу.

Для такой гиперболы уравнения асимптот будут: у = х и у = — х. Значит, асимптотами равносторонней гиперболы служат биссектрисы прямых углов, образованных осями координат, и тогда прямоугольник PQRS, которого диагонали лежат на асимптотах, будет квадрат (черт. 18).

Черт.18

Зададимся вопросом, каково будет уравнение гиперболы, если за оси координат  примем  асимптоты  ОТ и ОТ' (на чертеже 18-м мы изобразили часть правой ветви равносторонней гиперболы).

Пусть M есть какая-нибудь точка гиперболы, координаты которой х = OC и y = MC. Опустим из М на ОТ и ОТ'  перпендикуляры MD и ME. Тогда, если примем ОТ за ось x-ов и ОТ' за ось у-ов, то новые координаты будут: x' =OD=ME  и y'=MD=EO. Определим эти новые координаты как функции от прежних координат.
Для этого проведем еще CF_|_ ОТ и СK_|_ ОТ'. Заметив, что углы, обозначенные на чертеже цифрами 1, 2, 3 и 4, будут по 45°, мы из чертежа найдем:

OD = OF —DF= OF—СН= ОС cos 45° — MCcos 45°

и

ОЕ = OK + KE = OK+MH=ОСcos 45° + МCcos 45°,

т. е.

х' = х cos 45° — у cos 45° = (х — у) cos 45°

и

у' = х cos 45° + у cos 45° = (х + у) cos 45°;

откуда:

Уравнение равносторонней гиперболы x² — y² = a² можно изобразить так:

(х — у) (х + у) = a² Подставив сюда на место х — у и х + у их значения, найденые сейчас, получим:

Ho cos²45° = ¹/₂ значит, новое уравнение будет:

Мы видим теперь, что равносторонняя гипербола есть та самая кривая у = ^a/_x, которую мы рассматривали прежде (отдел 15 глава 7§ 348), только постоянному числу а надо дать значение ¹/₂ х²

Глава четвертая.

Парабола.

369. Определение и построение. Мы раньше говорили о параболе, как такой кривой, которая служит графиком функции у = ах² {в частности у = х²) (ч. I, отдел 6 глава 3§ 159). Теперь рассмотрим эту кривую в более общем виде и более подробно.

Параболе мы дадим теперь другое определение: параболой называется геометрическое место точек плоскости, из которых каждая одинаково удалена от данной точки (называемой фокусом) и от данной прямой (называемой директрисой).

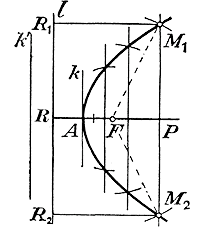
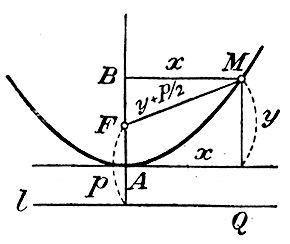
Такая точка называется вершиною, а бесконечная прямая, проходящая через F и А, называется осью параболы. Прямые M₁F , M₂F ..., соединяющие фокус с точками параболы, называются радиусами-векторами, отрезок RF, показывающий расстояние фокуса от директрисы, называется параметром параболы и обозначается обыкновенно буквой р.

Параллельные прямые можно брать направо от F как угодно далеко, так как для пересечения дуги с прямою необходимо и достаточно, чтобы расстояние FP от фокуса до прямой было меньше радиуса RР, а это всегда будет иметь место, как бы далеко направо от F ни была удалена параллельная прямая. Налево же от F параллельную прямую можно отодвигать только до крайнего положения, проходящего через вершину А, так как точки всякой прямой, параллельной l и расположенной левее от А (напр., точки прямой k'), отстоят от l, очевидно, меньше, чем от F.

Когда таким образом мы построим достаточное число точек, их можно все обвести непрерывною кривою, которая и будет парабола.

370. Уравнение параболы.

и, следовательно, уравнение параболы будет такое:

y² = 2рх.

То же самое мы нашли бы из чертежа, так как из тр - ка MBF видно:

Еоли обозначим дробь ¹/_2p буквою а, то уравнение параболы представится тогда так:

y = а x²,

а это и есть та функция, которую мы рассматривали прежде (ч. 1,отдел 6 глава 3 § 159). Теперь мы видим, что та кривая, которую мы тогда называли параболой, тождественна с кривой, которую мы теперь назвали параболой, только в прежней параболе осью симметрии служила ось у-ов, а в параболе, рассматриваемой теперь, ось симметрии есть ось x-ов. Чтобы определить положение фокуса и директрисы в параболе y = а x², надо найти ее параметр р из равенства:

¹/_2p = а; откуда р = ¹/_2a.

Значит, фокус лежит на оси у-ов выше начала координат на ¹/₂ р, а директриса параллельна оси x-ов и лежит ниже ее на ¹/₂ р (черт. 22).

Если вершина параболы не совпадает c началом координат, а находится в некоторой точке (m, n), и ось параболы параллельна оси х-ов, то уравнение кривой представится в таком виде:

( y — n)² = 2р ( х — m).

Если же ось параболы параллельна оси у-ов, то в уравнении надо х заменить на у и наоборот.

371. Следствия. Из уравнения y² = 2рх видно: 1) отрицательным значениям х не соответствует никакого вещественного значения у  это значит, что вся парабола расположена по правую сторону от оси y-ов.

2)  При всяком положительном значении  х ордината  у имеет 2 значения, отличающиеся  только знаками:  y = +√2рх и y = —√2рх . Значит, всякая прямая, перпендикулярная к оси x-ов и расположенная правеe оси y-ов, пересекается c параболой в двух точках, расположенных симметрично относительно оси x-ов, т. e. эта ось есть ось симметрии.

3)   При   всяком   значении   ординаты   у   (как положительном, так и отрицательном) абсцисса х получает определенное значение и только одно:    значит,   всякая   прямая, параллельная оси x-ов, пересекается с параболой и только в одной точке. Заметим, что всякая такая прямая называется диаметром параболы.

4) При неограниченном увеличении положительного значения х увеличивается неограниченно и абсолютная величина ординаты у, но увеличивается медленнее, чем абсцисса; так, если абсцисса увеличилась, положим, в 100 раз, то ордината увеличится только в 10 раз.

В гиперболе тангенс такого угла тоже равен  ^y/_x,   но там это выражение равно:

и при неограниченном увеличении х тангенс рассматриваемого угла стремится к дроби ^b/_a т. е. к тангенсу угла, образованного асимптотой о осью Ох (что и следует ожидать по свойству асимптоты).

372. Свойство касательной. Касательная к параболе есть биссектриса угла, образованного радиусом-вектором, проведенным из точки касания, и перпендикуляром, опущенным из нее  на директрису.

Доказательство вполне уподобляется тому, какое было дано для эллипса и для гиперболы.

Возьмем еще на секущей произвольную точку Р и проведем из нее Рq || M₁n и Рр || l. Из подобия четыреугольников PpMq и M₁mMn следует, что Mp = Mq.

Допустим теперь, что точка M₁неограниченно приближается к M. Тогда секущая приближается все ближе и ближе к касательной МТ, прямая M₁n приближается все более и более к перпендикулярности к MF (что следует из рассмотрения равнобедренного тр-ка FM₁n), a прямая Рр все время остается перпендикулярной к MN. Следовательно, когда секущая займет положение касательной МТ, прямоугольные тр-ки PMq и РрМ окажутся равными, и углы рМТ и TMq сделаются равными.

Это свойство дает простой способ проведения касательной, когда точка касания дана.

Проведем еще нормаль MS к параболе в точке M Так как / NMT=/ T₁MR и / NMT=/ TMF, то / T₁MR = / TMF, пoэтoму и / FMS= / SMR. Таким oбразом нормаль к параболе, прoведенная через какую-нибудь ее точку М, делит пополам угол, образованный радиусом-вектором и диаметром, проведенными из этой точки. На этом основано практическое применение параболических зеркал, как прожекторов; если в фокусе такого зеркала поставить источник света, то лучи его, отразившись от зеркала (по закону: угол падения равен углу отражения), пойдут по направлениям, параллельным оси зеркала.

373. Уравнение касательной. Если M₁ (x₁ , y₁) и M₂ (x₂ , y₂) две какие-нибудь точки параболы, то уравнение секущей, проходящей через них, есть (§ 352):

Координаты точек M₁ и M₂  должны удовлетворять уравнению пораболы:

y₁² = 2рx₁ и  y₂² = 2рx₂

откуда:

y₂² —  y₁² = 2р ( x₂— x₁)

или

(y₂ —  y₁ ) (y₂ +  y₁ ) = 2р ( x₂— x₁)

и следовательно,

Тогда уравнение секущей можно написать так:

Вообразим теперь, что точка M₂ приближается к M₁ и, наконец, сливается с ней. Тогда секущая обращается в касательную, и уравнение секущей делается уравнением касательной ( y₂ =  y₁ ) :

или

 y₁ y —  y₁² =  р x—  р x₁

Но

y₁² = 2 р x₁; следовательно,  y₁ y —  2 р x₁ =  р x—  р x₁. Откуда:

 y₁ y = р ( x + x₁)

374. Следствие. Найдем точку  пересечения  касательной  с осью x-ов. Для этого достаточно  в уравнения касательной положить   у = 0   и   найти   соответствующее   значение   х.   Тогда ,   получим:

0 = р ( x + x₁);      x = — x₁

Из чертежа 24-го видно, что абсцисса точки пересечения есть— АТ и x₁ = АВ;
значит,—АТ=—АВ и АТ=АВ. Таким образом, вершина параболы делит попoлам под касательную (так называется проекция касательной MN на ось х-ов). Это дает нам другой простой способ проведения касательной, когда точка касания задана.

375. Замечания. 1) Просматривая уравнения, выведенные нами для эллипса, гиперболы и параболы, мы видим, что все они 2-й степени с 2 неизвестными х и у. Благодаря особому расположению координатных осей, мы получили эти уравнения в упрощенном виде. В подробных курсах аналитической геометрии доказывается, что, во-перых, указанные кривые выражаются уравнениями 2-й степени при всяком расположении координатных осей, и, вo-вторых, наоборот, всякое уравнение 2-й степени с 2 неизвестными х и у, отнесенное к прямоугольным координатным осям, выражает собою вообще какую-нибудь из этих кривых. Поэтому кривые - эллипс, гипербола и парабола - называются кривыми 2-го порядка (т.е. кривыми, выражающимися уравнениями 2-й степени).

2) Доказано, что если боковую поверхность прямого кругового конуса пересечь какою-нибудь плоскостью, то в сечении получится (в зависимости от того, как проведена секущая плоскость) или эллипс (в частности окружность), или парабола или гипербола. Поэтому кривые эти называются также коническими  сечениями.