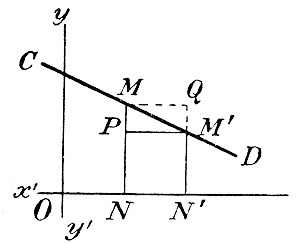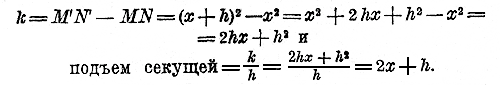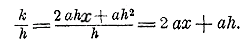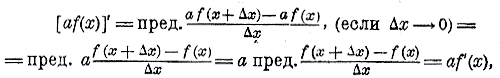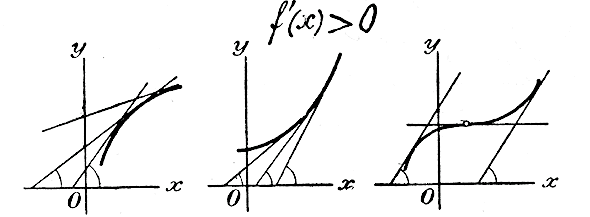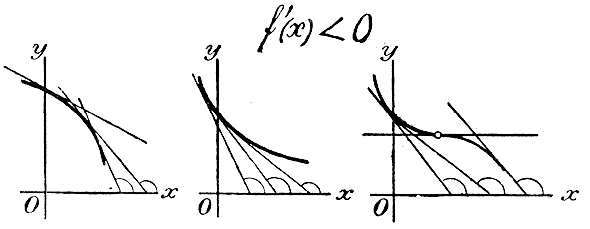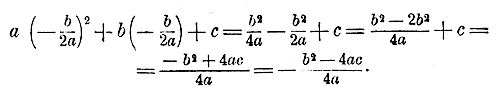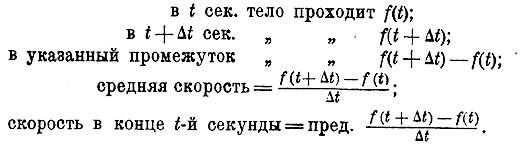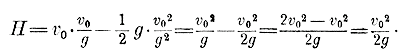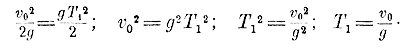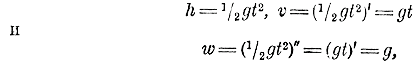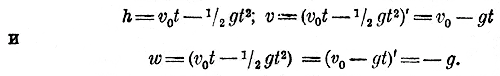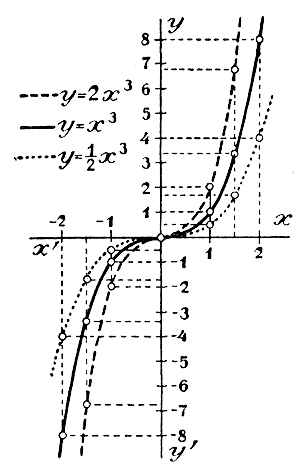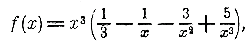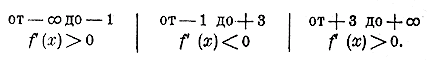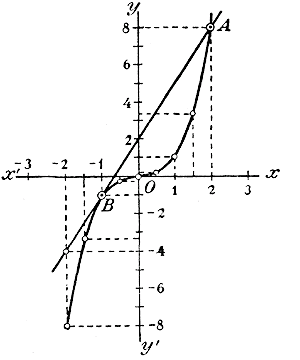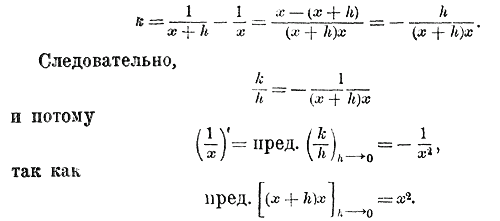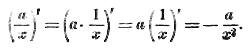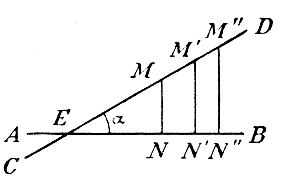
ОТДЕЛ   ПЯТНАДЦАТЫЙ.

ПРОИЗВОДНЫЕ ФУНКЦИИ.

Глава первая. Подъем прямой и кривой.
Глава вторая. Понятие о производной функции, как  выражающей подъем кривой.
Глава   третья. Общие обозначения.
Глава   четвертая. Признаки возрастания или убывания функций.
                               Признаки вогнутости или выпуклости кривой.
Глава пятая. Производная   как средство нахождения скорости и ускорения.
Глава шестая. Функция третьей степени.
Глава седьмая. Функция вида   y = ^a/_x

Глава первая.

Подъем прямой и кривой.

319. Подъем прямой. Подъемом какой-нибудь прямой CD  по отношению к горизонтальной прямой АВ называется иногда угол α, образуемый этими прямыми.

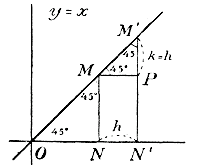
Точку М можно брать на прямой CD произвольно, так как если возьмем другие точки   M ',M'',..., то, проведя перпендикуляры M'N', M"N", мы получим подобные треугольники, из  которых видно, что

Если,   напр., MN = ¹/₁₀₀EN, то и M'N' = ¹/₁₀₀EN', M''N'' = ¹/₁₀₀EN''  и т. д.; тогда  можно сказать, что   подъем  прямой CD равен 1/100 (или что все равно— равен  1  метру на протяжении 100 метров по горизонтальному направлению).

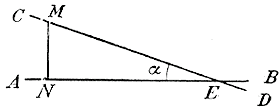
Уклон этот тоже измеряется чаще всего тангенсом угла α , образованного CD с AВ, так что

Можно условиться рассматривать уклон как отрицательный подъем; тогда, если MN = ¹/₂EN, то можно сказать, что уклон прямой CD равен ¹/₂, или — другими словами — что подъем прямой CD равен— ¹/₂.

Очевидно, что когда прямая CD не наклонна к AB, а параллельна ей или сливается с нею, тогда подъем равен нулю.

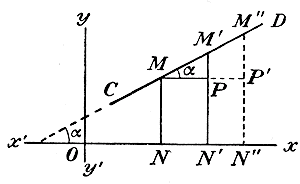
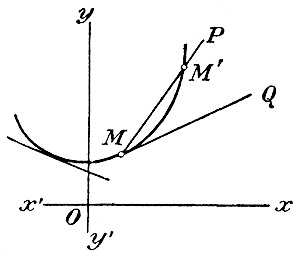
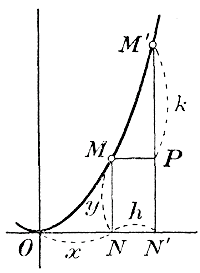
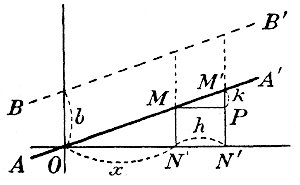
Для этого возьмем две какие-нибудь точки на прямой CD , напр..

М и M', проведем их ординаты MN и M'N' и прямую МР || Оx. Тогда мы получим прямоугольный тр-к ММ'Р, у которого угол M равен α. Следовательно, подъем прямой CD равен отношению М'Р к МР. Отрезок МР, равный NN', показывает, насколько увеличилась абсцисса ON при переходе от точки M к точке М'; отрезок М'Р показывает, насколько при этом переходе увеличилась ордината MN. Значит, отрезок MР, равный NN', есть приращение абсциссы, полученное ею при переходе от точки M к точке M', а M'Р—приращение ординаты, соответствующее приращению абсциссы на NN'. Конечно, если абсциссе ON дадим иное приращение, напр. NN", то и ордината MN получит иное приращение M"P', но тангенс угла α  по-прежнему   будет   отношение М"Р' к NN". Таким образом:

в   предположении,.. что  эти  два   приращения  соответствуют друг другу.

Положим, для  примера, что   прямая  CD есть график такой линейной функции:

y = — ¹/₃  x + 2

Дадим   абсциссе х произвольное   значение,   напр, х = 4;   тогда функция у будет равна:

y = — ¹/₃ • 4 + 2 = — ⁴/₃  + 2 = ²/₃

Пусть теперь абсцисса 4 получит какое-нибудь приращение, напр. 1. Тогда ордината у будет:

y = — ¹/₃ • 5 + 2 = — ⁵/₃  + 2 = ¹/₃

и, следовательно, приращение y окажется ¹/₃ — ²/₃ = —  ¹/₃

Поэтому              ^подъем    

Так оно и должно быть, потому что из уравнения прямой: y = — ¹/₃  x + 2 видно, что угловой коэффициент есть — ¹/₃  , а коэффициент этот, будучи равен тангенсу угла, образованного прямою c положительным направлением оси x - ов, выражает подъем прямой (в данном случае уклон).

320. Общее определение касательной к кривой.

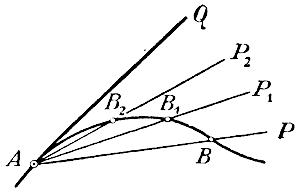
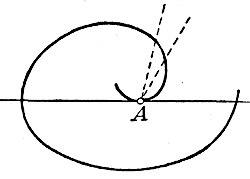
Если допустим, что точка В приближается к А неограниченно близко, то секущая приближается все более и более к некоторому предельному положению AQ так, что угол между прямою AQ и секущей делается и остается меньшим любого данного угла, как бы мал он ни был. Это предельное положение секущей называется касательной к кривой в точке А.

Вспомним, что когда в геометрии говорилось о касательной к окружности, то там она определялась как такая прямая, которая с окружностью имеет только одну общую точку. Это определение, верное относительно окружности, применимо однако не ко всякой кривой. Во-первых, прямая, имеющая с кривой только одну общую точку, может в этой точке пересекаться с кривой (незамкнутой, какова, напр., парабола); во-вторых, прямая—касающаяся кривой в какой-нибудь точке, может, кроме этой точки, иметь с кривою еще и другие общие точки (как это видно на чертеже).

Черт. 6

Определение, рассматривающее касательную, как предельное положение секущей, есть общее определение касательной, так как оно применимо ко всякой кривой.

321. Подъем кривой.

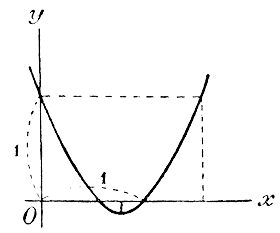
Условимся принимать подъем касательной, проведенной к кривой, за подъем самой кривой в точке касания.

322. Подъем параболы у = х².

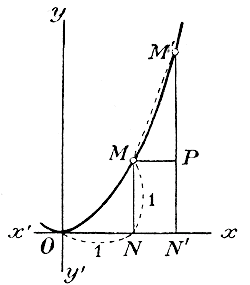
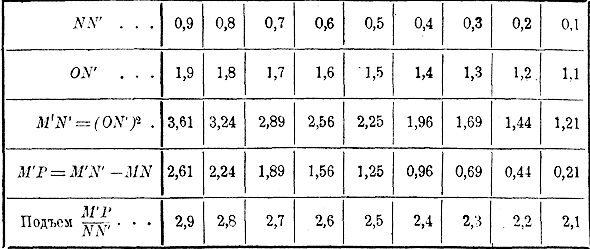
Пусть       NN' = 0,9.     Тогда   ON' = 1+ 0,9 = 1,9    и   M'N' =1,9 =3,61.

Значит, M'P =3,61 —1 = 2,61 и

подъем секущей = ^2,61 / _0,9 = 2,9.

Станем теперь уменьшать приращение NN', приближая, его к нулю: тогда точка M будет приближаться все ближе и ближе к точке М, и средний подъем кривой будет приближаться к равенству с подъемом кривой в точке М (с подъемом касательной в точке М). Будем, напр., для NN' назначать такие последовательно уменьшающиеся числа:

0,9;   0,8;   0,7;   0,6;   0,5;  ...  0,1.

Выпишем все числа, которые при этом получаются, в такой таблице:

Мы видим  из этой таблицы, что по  мере приближения точки М'   к   М   подъем   секущей   все   уменьшается,  приближаясь все более и более к числу 2, так что весьма вероятно, что подъем секущей (средний подъем кривой) стремится к пределу 2, когда приращение NN'—>0. Если это так, то подъем параболы в точке М, имеющей абсциссу 1 и ординату 1, равен 2. Мы сейчас увидим, что это действительно так.

Положим теперь, что h —> 0, следовательно, точка M' неограниченно  приближается к M. Найдем предел, к которому при этом стремится отношение ^k/_h, равное   сумме   2х + h.   Так как х остается без изменения, то очевидно, что если h —> 0, то 2х + h —> 2х.

Значит, подъем параболы в точке с абсциссой х равен 2х. Например, для точки с абсциссой 1 подъем будет 2•1 = 2, что мы и предвидели, когда вычисляли подъем для уменьшающихся приращений: 0,9; 0,8; 0,7;... 0,1. Для точки с абсциссой 2 подъем будет 2•2 = 4, для точки с абсциссой 2 ¹/₂ он окажется 2 ¹/₂ • 2 = 5 и т. п.

Глава вторая.

Понятие о производной функции, как  выражающей подъем кривой.

323. Определение и обозначение. Мы видели в предыдущем параграфе, что подъем кривой зависит от величины абсциссы той точки, в которой определяется подъем: он есть некоторая функция от абциссы х.

Функция, выражающая подъем кривой в какой нибудь-точке ее в зависимости от абсциссы этой точки, называется производной функцией от той функции, которая выражает эту кривую.

Так, для параболы  у = х², как мы видели, подъем кривой в точке с абциссой х равен 2х; эта функция 2х называется производной (функцией) от функции х².

Производную функцию принято обозначать посредством знака  ' , поставленного с правой стороны над выражением той функции, от которой берется производная. Так, если функция обозначена одною буквой у, то производная от нее обозначается y' если функция задана каким-нибудь алгебраическим выражением, то производную можно обозначать тем же выражением, но со знаком '. Так, можно написать: (х²)' = 2х, что читается так: производная от х² равна 2х.

324. Производная от постоянного числа.

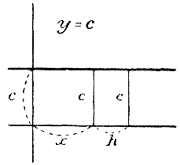
И действительно, какое бы приращение h мы не дали абсциссе х, ордината у остается неизменной (равной с): значит, приращение к ординаты всегда равно нулю, а потому и отношение ^k/_h при всяком h равно нулю.

325.  Производная   от   функции у = х.  

подъем прямой = ^k/_h  =  ^h/_h = 1.

Таким образом:

x' = 1

т. е. производная от переменного независимого равна 1.

Это  же  видно   и  из уравнения у = х, в котором  угловой коэффициент, выражающий подъем, есть 1.

326.  Производная от функции  у = ах.

т. е. производная от функции у = ах равна угловому коэффициенту.

327.Производная от функции   у = ах + b.   

Эта функция выражается прямой BE ( Черт. 12 ), отсекающей от оси y-ов отрезок b и имеющей угловой коэффициент а. Если дадим абсциссе х приращение x, то ордината у получит приращение k, равное

k = [а(х + h) + b] — (ax + b) = ax + ah + b — ax — b = ah.

Следовательно,

(ax + b) ' = подъем = ^k/_h = ^ah/_h = а,

что и надо было ожидать, так как подъем прямой во всякой ее точке равен угловому коэффициенту.

Обратим внимание на то, что в этом примере производная от суммы ax + b равна сумме производных от слагаемых.

Действительно, (ах)' = а, b' = 0 и а + 0 = а; а это есть (ax + b) ' .

328. Производная от функции у = ах². Эта функция геометрически выражается, как мы знаем (ч. I, отдел 6, глава 3 § 158), параболой. Чтобы найти подъем этой параболы в точке с абсциссой х (черт. 9), дадим этой абсциссе приращение h; тогда ордината у получит приращение

k = а(х + h)²— ах² = ах² + 2аhx + аh² — ах² = 2аhx + аh².

Следовательно, средний подъем параболы у = ах² на участке от точки с абсциссой х до точки с абсциссой x + h, будет

Если h —> 0, то и ah —> 0, a 2ах остается без изменения; след., подъем будет:

(ах²)' = пред. ^k/_h = пред. (2аx + аh) = 2аx.

Таким образом, производная от одночлена ах² равна показателю при х, умноженному на такой же одночлен, у которою только показатель уменьшен на 1.

Так:

(х²)' = 2х;     (2х²)' = 4х;     (3х²)' = 6х;     и т. п.

Глава   третья.

Общие обозначения.

329. Общее   обозначение   функциональной    зависимости.

Чтобы кратко обозначить, что переменное число у есть функция от переменного независимого числа х, принято писать так:

y = f(x).

Здесь буква f есть первая буква французского слова „fonction", что значит: „функция". Следовательно, равенство это читается так: у есть функция от х. Какая это функция, этим обозначением не выражается; выражается только, что у есть некоторая функция от х. Напр., в частных случаях может быть:

f(x) = 3x;     f(x) = х²; f(x) = aх²;    f(x) = х² — 2x + 5    и т. п.

Вместо f иногда употребляются буквы F, φ, Ф и некоторые другие. Ecли, напр., написано:

y = f(x), u = F(x),

то этим выражено, что переменные числа у и u суть некоторые функции от одного и того же переменного числа х, но функции эти различны.

Если функция обозначена f(x), то ее производную можно обозначить f' (x). Так, из равенства: f(x) = aх² выводим: f' (x) = 2ах.

330.  Общее обозначение приращений. До сего  времени мы обозначали  приращение  переменного  независимого  числа х (аргумента функции) буквою h, а  соответствующее   приращение самой   функции  у буквою k.  Принято также  обозначать слово „приращение" греческою буквою Δ (дельта,), поставленною перед обозначением того переменного независимого или той функции, которая получает приращение. Так, Δ x означает: „приращение числа х"; равным образом Δ f(x) означает: „приращение функции f(x)". Значит, в таких обозначениях буква Δ не означает числа, а заменяет слово „приращение", подобно тому, как в выражении f(x) буква f не означает числа, а только слово „функция".

331. Определение производной как предела отношения приращений.

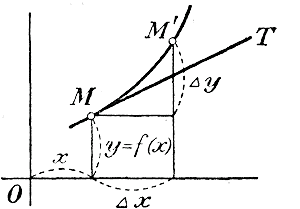
Предел этого среднего подъема, когда  Δх —> 0, есть подъем кривой в точке M (подъем касательной МТ) и называется, как мы говорили, производной функцией от f(x). Значит, мы можем написать:

f' (x) = пред.^Δу/_Δх , если Δх —> 0.

Так как Δу = f(х + Δх) — f(x), то это равенство можно переписать так:

Таким образом можно высказать следующее определение производной:

Производной функцией от функции f (x) называется предел, к которому стремится отношение приращения этой функции к соответствующему приращению переменного независимого х, если это последнее приращение стремится к нулю.

332. Производная от произведения постояного числа на функцию.

Пусть y = a f(x), где а есть постоянное  число и f(x) какая-нибудь функция. Согласно данному сейчас определению, мы будем иметь:

что можно высказать так:

Производная от произведения какой-нибудь функции на постоянное число равна произведению этого постоянною числа на производную от функции.

Напр.,    (ах)' = ах' = а •1 = а;    (ах²)' — а(х²)' = а•2х = 2ах.

333. Производная от алгебраической суммы. Мы уже видели раньше (§ 327) что

(ах + b)' = (ах)' + b' = а + 0 = а,

т. е. что производная от суммы равна сумме производных от слагаемых. Убедимся теперь в общности этого свойства. Пусть u, v и w будут какие-нибудь функции от одного и того же переменного независимого х и пусть у есть алгебраическая сумма этих функций, напр., такая:

у = u + v — w.

Если х получит приращение Δx, то функции u, v , w и у получат некоторые приращения  Δu, Δv, Δw; и Δy, причем очевидно, что в нашем примере:

Δ у =Δ u + Δ v — Δ w.

Следовательно,

Так как предел алгебраической суммы равен той же сумме пределов слагаемых, то когда Δx—>0:

Ду                     Дм  ,                  Ли                      &w

пред.^{Δ у}/_Δх = пред.^{Δ u}/_Δx + пред.^{Δ v}/_Δx — пред.^{Δ w}/_Δх,

т. е.

у' = u' + v' — w'

Таким образом:

Производная от  алгебраической суммы равна той же сумме производных от слагаемых.

Пользуясь этим свойством, мы легко можем найти производную от трехчлена 2-й степени. Напр.:

1) (2х² + 5х — 3)' = (2х²)' + (5х)' — (3)' = 4x + 5 — 0 = 4x + 5.

2) (¹/₂  х² + 2)' = (¹/₂  х²) ' + 2' = ¹/₂  • 2x+ 0 = х.

Глава   четвертая.

Признаки возрастания или убывания функций.
Признаки вогнутости или выпуклости кривой.

334. Maximum и minimum.

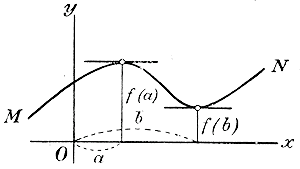
Из того же чертежа видно, что при дальнейшем возрастании х функция убывает до некоторого значения f(b) при х = b, а затем возрастает. Тогда значение f(b) называется minimum функции, или ее наименьшим значением, причем опять-таки разумеется, что это значение не есть наименьшее из всех возможных, а только из всех соседних значений как справа, так и слева.

Иногда случается, что при возрастании х от — ∞ до + ∞ функция все возрастает, или все убывает, или же остается неизменной; тогда функция не имеет ни maximum, ни minimum. Таковы, напр., линейная функция у = ах + b, показательная функция у = а^х (ч. I, отдел 11 глава 5 чертеж) и логарифмическая функция y = log _a x (ч. I, отдел 12 глава 1 чертеж).

335. Признаки возрастания или убывания функций. Если при возрастании х функция  f (x) тоже возрастает (такая функция называется возрастающей), то, как видно из чертежа 15-го,

Возрастающая   функция

Черт.15

касательные, проведенные к кривой, изображающей функцию, образуют о положительным направлением оси х-ов острые углы, причем для некоторых отдельных (особых) точек кривой (напр., для точки, указанной кружком, чертеж 15-й, правый) касательная может образовать и угол в 0°.  

Если же при возрастании х функция убывает (такая функция называется убывающей),

Убывающая   функция

Черт.16

то касательные (черт. 16) образуют с положительным направлением оси x-ов тупые углы, причем для некоторых отдельных точек кривой касательная может образовать и угол 0° (черт. 16-й, правый). Так как тангенсы острых углов положительны, а тупых — отрицательны, и тангенсы углов, образованных касательными с положительным направлением оси х-ов, равны производным, то мы приходим к таким выводам:

1)  Если f(x) при изменении х между какими-нибудь  границами есть функция возрастающая, то ее производная для значений   х, лежащих   между   этими   границами,   положительна,   причем   для   отдельных   значений   х   она    может равняться нулю (черт. 15).

2)  Если f(x) при изменении х между какими-нибудь  границами, есть функция убывающая, то ее производная для значений х, лежащих между этими границами, отрицательна, причем   для   отдельных   значений   х   она   может   равняться нулю (черт.16).

3)  Наконец, если f(x)  при изменении х между какими-нибудь границами  не изменяется (есть постоянное число), то ее производная для значений х, лежащих между этими границами, равна нулю, так как производная постоянного числа есть нуль.

Заметив все это, мы можем высказать и обратные предложения:

1)  Если при изменении х между какими-нибудь  границами производная  положительна  (причем   для  отдельных  значений она может равняться нулю), то функция между этими границами возрастает.

2)  Если при изменении х между  какими-нибудь  границами производная   отрицательна   (причем для   отдельных   значений она  может  равняться  нулю), то функция между этими границами убывает.

3)  Если при изменении х между  какими-нибудь  границами производная остается равной нулю, то функция равна постоянному  числу.

Из чертежа 14-го видно, что если при некотором значении х =  а (или х = b) функция y=f(x) имеет наибольшее или. наименьшее значение, то касательная к кривой, изображающей функцию, проведенная через точку с абсциссой а (или b), параллельна оси x - ов (другими словами, образует с нею угол в 0°); следовательно, производная функция при х = а (или х = b) должна   равняться нулю. Но так как производная может равняться нулю и в других случаях (черт. 15 правый или черт. 16 правый), то обратное предложение нельзя считать верным, т. е. если при некотором значении х = а производная равна нулю, то из этого одного еще не следует, чтобы при х = а функция имела наибольшее или наименьшее значение.

Для примера приложим все сказанное к такому трехчлену: второй степени:

           y = 2х² — 3х + l.

Производная этого трехчлена для всякого значения х равна

у' = 4х — 3.

Чтобы узнать, для каких значений х эта производная положительна и для каких отрицательна, надо решить два неравенства:

1) 4х — 3 > 0; откуда х > ³/₄:

2) 4х — 3 < 0; откуда х < ³/₄:

Значит, для всех значений х, больших ³/₄, трехчлен возрастает, а для всех значений х, меньших ³/₄ он убывает. Следовательно, при х = ³/₄ трехчлен переходит через наименьшее значение, которое равно:

2 • (³/₄ )² — 3 • (³/₄ ) + l =  ⁹/₈ —  ⁹/₄ + l = — ¹/₈

Следующая  таблица  и  чертеж  17-й  наглядно  изображают процесс изменения данного трехчлена:

 y = 2х² — 3х + l

Черт.17

Возьмем еще   трехчлен в общем виде:

у = ax²  + bx + c.

Производная этого трехчлена равна:

у' = 2ах + b.

Решим теперь два следующих неравенства:

1) 2ах + b > 0;   откуда:  х > — ^b/_2a,   если а > 0  и   х < — ^b/_2a,   если а < 0;

2) 2ах + b < 0;   откуда:  х < — ^b/_2a,   если а > 0  и   х > — ^b/_2a,   если а < 0;

Значит, если а > 0, то трехчлен возрастает при х > — ^b/_2a  и убывает при х < — ^b/_2a;
если а < 0, то, наоборот, при х > — ^b/_2a трехчлен убывает, а при х < — ^b/_2a он возрастает

Отсюда, следует, что при х = — ^b/_2a  трехчлен получает наименьшее значение при а > 0  и наибольшее при а < 0; и то и другое равно:

Все это вполне согласуется со сказанным нами ранее в § 227,  ч. I. отдел 9 глава 2

336. Признаки выпуклости или вогнутости кривой. Предположим, что  при возрастании х производная от данной функции тоже возрастает. В геометрическом смысле это значит, что при возрастании х подъем кривой, выражающей данную функцию, увеличивается; другими словами, увеличиваются тангенсы углов, образованных касательными с поле жительным направлением оси х-ов. Но если увеличиваются тангенсы, то и самые углы увеличиваются

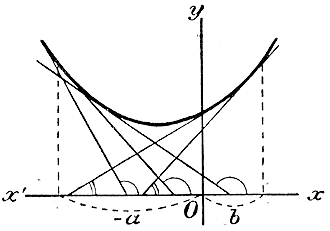
Черт.18

Такой случай изображен на чертеже 18-м на котором видно, что при возрастании абсциссы х точки касания от — а до + b углы, образованные касательными с положительным направлением оси х-ов, становятся все больше и больше, вследствие чего вогнутость кривой обращена кверху (а выпуклость книзу).

Если же допустим, что при возрастании х производная уменьшается, то  это значит,   что уменьшается подъем   кривой,   и, значит, уменьшаются углы, образованные касательными о положительным направлением оси х-ов.

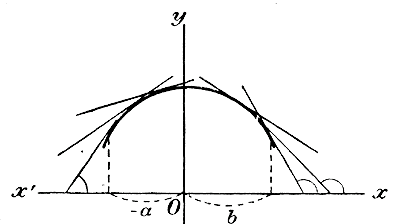
Черт.19

Такой случай изображен на чертеже 19-м из которого видно, что при возрастании х от  — а до + b углы, образованные касательными, уменьшаются, вследствие чего вогнутость кривой обращена вниз (выпуклость вверх).

Таким образом, если при возрастании х производная возрастает, то вогнутость кривой направлена вверх, а если она при этом убывает,  то вогнутость направлена вниз.

Если же производная не возрастает и не убывает, то кривая не имеет выпуклости (т. е. она прямая).

Напр., производная трехчлена  2х² — 3х + l , о котором мы говорили в предыдущем параграфе, есть 4х — 3. Очевидно, она возрастает при возрастании х, и вогнутость параболы, изображающей   этот   трехчлен,   направлена   вверх (черт. 17).

Наоборот, трехчлен — х² + х + 2 имеет производную — 2х + 1, которая при возрастании х убывает, вследствие чего вогнутость параболы обращена вниз.

Глава пятая.

Производная   как средство нахождения скорости и ускорения.

337. Средняя скорость. Движение материальной точки называется переменным, или неравномерным, если в одинаковые промежутки времени точка проходит неодинаковые пространcтва ,   причем оно называется    ускорительным,  если пространства, проходимые в равные промежутки времени, следующие друг за другом, все увеличиваются, и замедлительным, если эти пространства все уменьшаются.

Напр., всякое тело, свободно падающее с какой-нибудь высоты, движется ускоренно, проходя в первую секунду 4,9 м (приблизительно), во вторую секунду 14,7 м, в третью 24,5 м и т. д. Наоборот, тело, брошенное вертикально вверх, движется эамедлительно, проходя в каждую следующую секунду пространства все меньшие и меньшие, пока, достигнув некоторой наибольшей высоты, не станет падать вниз ускоренно;

При равномерном движении скорость остается одна и та же во все время движения, при переменном же движении она меняется с каждым моментом времени. Поэтому, говоря о скорости переменного движения, необходимо добавлять, к какому моменту мы относим эту скорость. Напр., при падении тела скорость в конце 1-й секунды от начала падения будет одна, в конце 2-й секунды другая, в конце 2 ¹/₂ секунд третья и т. д. Чтобы выяснить, что называется скоростью переменного движения в данныйй момент времени, предварительно разъясним, что такое средняя скорость переменного движения за данный промежуток времени..

Пусть железнодорожный поезд вышел со станции в 12 ч. дня и пришел на следующую станцию, отстоящую на 15 км от первой, в 12 ч. 20 м. дня. Значит, в течение промежутка времени, равного 20 мин., поезд прошел путь в 15 км. Если бы в течение этих 20 минут поезд двигался вполне равномерно и прошел бы тот же самый путь в 15 км, то скорость такого равномерного движения былабы 15 : 20 =  ³/₄ км в мин. или ³/₄  • 60 = 45 км в час. Эта скорость и есть средняя для промежутка времени от 12 часов до 12 ч. 20 м.

Таким образом:

Среднею скоростью переменною движения за данный промежуток времени называется скорость такого равномерного движения, при котором тело в тот же промежуток времени прошло бы путь такой же длины, какой оно прошло при переменном движении.

Пусть за данный промежуток времени, продолжавшийся t единиц времени, тело прошло переменным движением е единиц длины; тогда, если бы оно двигалось равномерно, то скорость такого равномерного движения была бы равна частному е : t. Это частное и выражает среднюю скорость за данный промежуток времени.

338.   Скорость в   данный момент. В течение данного промежутка времени движущееся неравномерно тело, конечно, имело множество различных  скоростей, из которых некоторые были меньше, а другие больше средней скорости; но ясно, что чем меньше промежуток, за который вычисляется средняя скорость, тем меньше разница между этою среднею скоростью и каждою из истинных  скоростей,  которые  тело  имело за этот промежуток.

Поэтому понятно будет следующее определение:

За величину истинной скорости переменного движения в данный момент времени принимается предел, к которому стремится средняя скорость, вычисленная для промежутка времени, непосредственно следующего за данным моментом (или ему предшествующего - все равно), если этот промежуток стремится к нулю.

339.  Свободное падение тела. Для примера рассмотрим свободное падение тела с некоторой высоты. Из опыта найдено, что  пространство   (обыкновенно,   оно  обозначается  буквою h), которое при этом тело проходит в t секунд, выражается (если не считать сопротивления воздуха) формулой:

h =  ¹/₂ gt²,

где g есть постоянное число, равное приблизительно 980 см = 9,8 м (около 10 м). Пользуясь этой формулой, вычислим скорость падения, положим, в конце 2-й секунды от начала падения. Для этого возьмем какой-нибудь небольшой промежуток времени, следующий за концом 2-й секунды, напр., в 0,1 сек., и найдем среднюю скорость падения за этот промежуток. Для этого надо найти пространство, которое падающее тело проходит за этот промежуток, и разделить его на 0,1. Пространство это мы найдем так:

в 2 сек. тело проходит ¹/₂ g • 2² = 2g;

в 2,1сек.   „           „        ¹/₂ g • 2,1² = ¹/₂ g • 4,41 = 2,205g

следовательно, в промежуток от конца 2-й сек. до конца 2,1 сек. тело проходит
2,205g— 2g = 0,205g;

средняя скорость за этот промежуток = ^0,205g/_0,1 = 2,05g.

Подставив  вместо g число 980 см, мы получим для средней скорости число 2009 см = 20 м 9 см в секунду,

Уменьшим, наконец, промежуток; напр., возьмем 0,01 секунды. Тогда:

в 2 сек. тело проходит ¹/₂ g • 2² = 2g;

в 2,1сек.   „           „        ¹/₂ g • 2,01² = ¹/₂ g • 4,0401 = 2,02005g

в промежуток от конца 2-й сек. до конца 2,01 сек. тело проходит

2,02005g — 2g = 0,02005g;

средняя скорость за этот промежуток = ^0,02005g/_0,01 = 2,005g..

Мы видим, что средняя скорость приблизилась к 2g. Если бы еще уменьшить промежуток, напр., взять, 0,001 сек., то средняя скорость еще более приблизилась бы к 2g (она тогда была бы 2,0005g ), так что надо ожидать, что предел, к которому стремится средняя скорость (когда промежуток времени стремится к нулю), равен в точности 2g. Чтобы убедиться в этом, мы возьмем промежуток времени, выраженный буквою, составим формулу, выражающую среднюю скорость падения тела для этого буквеннного промежутка, и затем найдем предел этой формулы, когда промежуток будет стремиться к нулю. Вместе с тем мы обобщим теперь вопрос: будем искать скорость падения тела не в конце 2-й секунды, а в конце t -й секунды (от начала падения).

Пусть мы берем промежуток времени в k секунд (k— какая-нибудь малая дробь), следующий за концом t -й сек., т. е. промежуток от конца t -й сек. до конца (t+k)-й сек. Среднюю скорость за этот промежуток мы находим так же, как находили ее сейчас для конца 2-й сек., а именно:

Найдем предел, к которому стремится средняя скорость, когда k—>0. Так как предел суммы равен сумме пределов слагаемых и gt есть число постоянное, а предел слагаемого  ¹/₂gk есть 0, то, если k—>0,

предел средней скорости = gt.

В частности для конца 2-й секунда этот предел равен g • 2 = 2g, как мы и ожидали раньше.

Так как предел средней скорости принимается за величину истинной скорости в момент, от которого мы брали промежуток времени, то, обозначая эту скорость буквою v, можем написать:

v = gt.

Заметив, что произведение gt есть производная от функции ¹/₂ gt², выражающей пространство h, проходимое падающим телом в t секунд, мы можем написать:

v = ( ¹/₂ gt² )' = gt

Таким образом на этом примере мы приходим к заключению:

Скорость переменною движения в конце t -й секунды равна производной от функции, выражающей зависимость пространства, проходимою при этом движении, от времени t , в течение которого это пространство проходится.

Мы сейчас увидим, что это заключение применимо ко всякому движению.

340. Соотношение между скоростью и производной. Пусть вообще дано движение, в котором пространство е, проходимое телом в t секунд, выражается некоторой функцией от времени t:

e = f(t).

Найдем скорость этого движения в конце t-й секунды. Для этого дадим времени t какое-нибудь приращение Δ t сек., вычислим среднюю скорость для промежутка времени от конца t-й секунды до конца (t + Δ t)-й сек. и затем найдем предел этой средней скорости, когда Δ t—>0:

Разность f (t + Δ t) — f (t) выражает приращение функции f(t), соответствующее приращению переменного независимого t на Δ t. Предел отношения этого приращения к приращению переменногo   независимого  называется производной  функцией от f(t).

Значит, обозначив скорость в конце t-й секунды буквой v, мы можем последнее выведенное нами равенство переписать так:

v = f'(t).

Мы видим таким образом, что заключение, которое мы вывели для скорости падения тела, применимо ко всякому движению.

341.   Движение  тела,  брошенного вертикально вверх.  Как пример применения найденной нами зависимости между производной и скоростью рассмотрим еще движение тела, брошенного вертикально вверх с начальною скоростью v₀ (см в секунду). Из физики известно, что высота h, на которую такое тело подымается в t сек., выражается следующей функцией от времени:

h = v₀t — ¹/₂ gt²,

где g есть то постоянное число (равное приблизительно 980 см), которое мы встречали в формулах свободного падения тела. Скорость v такого движения в конце t-й секунды, согласно сказанному в предыдущем §, выразится так:

v = ( v₀t — ¹/₂ gt² )'

Производная от алгебраической суммы равна той же сумме производных от слагаемых  (§ 333); поэтому:

v = ( v₀ t)' — ( ¹/₂ gt² )'

Мы видели (§§ 326, 328), что (ах)'= а и (ах² )' = 2ах. Значит, заменяя х на t, мы будем иметь:

( v₀ t)'  = v₀ t    и    ( ¹/₂ gt² )'  = 2 • ¹/₂ gt = gt

Следовательно,

v = v₀ — gt.

Из этой формулы видно, что с возрастанием времени скорость уменьшается и притом равномерно, так как с каждым увеличением времени на одну единицу скорость уменьшается на одну и ту же величину g. Такое движение называется равномерно-замедлительным, а величина, на которую скорость уменьшается в течение каждой секунды, называется отрицательным ускорением этого движения (при свободном падении тела ускорение положительное). Два движения — равномерно-ускорительное и равномерно-замедлительное носят общее название „равномерно-переменное движение".

Когда время настолько увеличится, что разность v₀ — gt, a следовательно, и скорость v, обратятся в нуль, тогда начнется обратное движение — равномерно-ускоренное падение вниз.

Разрешим 4 следующие вопроса: 1) как велико время Т, в течение которого тело достигнет наивысшей точки; 2) какова высота Н, на которую оно при этом поднимается; 3) какое время T₁понадобится, чтобы тело с верхней точки упало вниз, и 4) какую скорость  v  оно приобретет при возвращении назад.

1) Так как при наивысшем поднятии скорость v должна обратиться в нуль, то время Т мы найдем из уравнения:

v₀ — gТ= 0,

откуда:

Напр., при начальной скорости v₀ = 4900 см в секунду, это время равно 4900 : 980 = 5 сек.

2) Высоту поднятия H получим из уравнения h = v₀ t — ¹/₂ gt², если на место t подставим :

Напр., при начальной скорости 4900 см в сек. получим:

3) Для решения третьего и четвертого вопросов надо пользоваться формулами свободного падения тел:

h = ¹/₂ gt², и v = gt.

Так как высота H, с которой тело падает вниз, нам уже известна, то время падения T₁найдется из формулы пространства, если вместо h подставим    :

Таким обpазом, время падения с верхней точки вниз равно времени поднятия.

4) Скорость v, которую тело получит при возвращении назад,  найдется  из  формулы  скорости: v = gt, если   вместо t подставим   :

Таким обрааом тело, возвратившись назад, приобретает ту же скорость, с какою началось поднятие вверх.

Должно однако иметь в виду, что эти выводы верны лишь в предположении, что движение совершается в безвоздушном пространстве, так как сопротивление воздуха уменьшает высоту поднятия и уменьшает скорость в конце возвращения.

342. Ускорение при движении. При равномерно-переменном движении ускорением называется положительное или отрицательное приращение скорости в одну единицу времени. При движении равномерно-переменном это приращение одинаково для каждой единицы времени; так. при свободном падении тела оно равно круглым числом +10 м в секунду, при движении тела, брошенного вертикально вверх, оно составляет около —10 м в секунду. Но движение может быть и не равномерно-переменное, когда изменение скорости в течение равных промежутков времени не одно и то же. В таком движении каждому моменту соответствует свое особое ускорение. Чтобы уяснить себе, что при движении неравномерно-переменном принимается за меру ускорения в данный момент, надо предварительно определить так называемое среднее ускорение за данный промежуток времени.

Положим, что за промежуток времени Δ t, следугощий за концом t-й единицы времени, скорость v данного движения получила приращение (положительное или отрицательное) Δ v. Тогда частное Δ v : Δ t будет означать прирашение скорости в одну единицу времени, если в течение промежутка Δ t скорость изменяется равномерно. Частное это называется средним ускорением движения за промежуток Δ t, следующий за концом t-й единицы времени. В действительности скорость v изменялась за этот промежуток неравномерно, и потому в продолжение его могло быть бесчисленное множество различных по величине ускорений. Но очевидно, что разность между средним ускорением и каждым из этих ускорений тем меньше, чем меньше промежуток Δ t, для которого вычислено среднее ускорение. Поэтому мы можем дать такое определение:

За ускорение неравномерно-переменною движения в данный момент принимается предел, к которому стремится среднее ускорение, вычисленное для промежутка времени, следующею за данным моментом (или ему предшествующего - все равно), когда этот промежуток стремится к нулю.

Таким образом,

ускорение в данный момент = пред. ^{Δ v}/_{Δ t}  ,      если Δ t—>0.

343. Соотношение между ускорением и производной от скорости.

Положим, что скорость v есть некоторая функция от времени:

v = f(t)

Тогда приращение Δ v, полученное скоростью в течение промежутка Δ t, следующего за концом t-й единицы времени, может выразиться так:

Δ v =   f(t + Δ t)  —  f(t);

следовательно,

Значит, ускорение в конце t-й единицы времени (обозначим его w), будет:

Но предел этот есть производная от f(t); поэтому:

если v = f(t), то w = f '(t),

что можно высказать так:

Ускорение равно производной от функции, выражающей скорость в зависимости от времени.

Как мы видели (§ 340), функция, выражающая скорость, сама есть производная от пространства, выраженного в зависимости от времени; значит, ускорение равно производной от этой производной, т. е. так называемой второй производной от пространства (обозначается знаком " ).

Например, при свободном падении тела (§ 339):

т. е. ускорение постоянно для всех моментов и равно g (= 980 см в сек.).

При движении тела, брошенного вертикально вверх (§ 341):

Вообще, если пространство е, проходимое телом в t единиц времени, выражаетоя трехчленом 2-й степени:

e = at²  + bt + c ,       то

v = (at²  + bt + c)' = 2at + b   

и

w = (at²  + bt + c)" = (2at + b)' = 2а.

Глава шестая.

Функция третьей степени.

344. Производная от функций   у = х³  и  у = ах³. Главнейшие особенности этих функций мы уже рассмотрели ранее (ч. I, отдел 6 глава 5 §§ 162, 163); тогда же мы построили графики этих функций (черт. 20). Найдем теперь их производные.

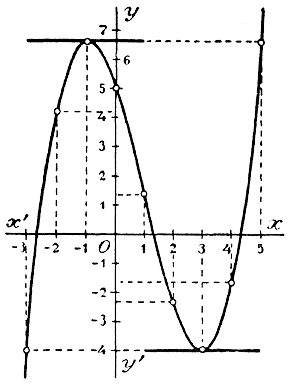
Черт.20

Положим, что переменному независимому числу мы дали какое-нибудь приращение h, начиная от произвольного его значения х. Тогда функция х³ получит некоторое приращение k, равное:

k = (х + h)³ — х³ = 3hх² + 3h²х + h³

Следовательно,

^k/_h = 3х² + 3hх + h²

Если

h—>0, то 3hx —> 0 и h²—>0;

поэтому:

(х³)'  =  пред. ^k/_h = 3х².

Производную от функции у = ах³ мы легко найдем, основываясь на том, что (§ 332):

[af(x)]' = af(x).

Следовательно,

(ах³)' = а (х³)'  = а • 3х² = 3ах².

Так:

(¹/₂ х³)' = 3•¹/₂ х² = ³/₂ х²;        (2ах³)' = 3• 2ах² = 6ах².

Применение.   Воспользуемся   этими   производными   для определения  направления  выпуклости и  вогнутости   кривых:

у = х³,  у  = ¹/₂ х³  ,   у = 2х³ (черт. 20).

Производные этих функций, равные 3х²,   ³/₂ х²   и   6х², очевидно, возрастают при возрастании положительного значения х и убывают при возрастании отрицательного значения х. Так, если дадим числу х возрастающие значения: — 2,—1, 0, 1, 2..., то производная 3х² будет: 12, 3, 0, 3, 12..., т. е. она убывает, пока отрицательные значения числа х возрастают, и возрастает при возрастании положительных значений х. Вследствие этого, согласно признакам вогнутости кривых (§ 336), рассматриваемые кривые обращены вогнутостью вверх для положительных значений х и вниз, для отрицательных, что мы и видим на чертеже 20. При переходе через значение х = 0 кривые меняют выпуклость на вогнутость и потому в начале координат они имеют так называемую  точку перегиба.

345. Исследование  полной   функции  третьей  степени   (на частных примерах).

Пример 1-й.     f(x) = ¹/₃ х³ — х² — 3x + 5.

Желательно исследовать эту функцию, т. е. решить следующие вопросы:

1) всегда ли функция возможна и получает ли она при данном значении х только одно значение, или несколько;
2) при каких значениях х функция возрастает и при каких убывает;
3) найти maximum и minimum функции, если таковые существуют;
4) найти, если можно, нулевые значения функции (корни уравнения ¹/₃ х³ — х² — 3x + 5 = 0) и
5) найти предельные значения функции при х = ± ∞ и при х = 0.

Последний вопрос решается без помощи производной. Подставив вместо х число 0, мы прямо найдем, что тогда данная функция обращается в + 5. С другой стороны, представив функцию в виде произведения:

мы видим, что когда х —> ± ∞, многочлен, стоящий внутри скобок, имеет пределом  ¹/₃, а множимое х³ стремится к + ∞, если х—>+ ∞ и к — ∞, если х —>∞.
Значит, f(x)—>+ ∞ в первом случае и к — ∞ во втором.

Для решения вопроса о возрастании или убывании функции, надо составить ее производную. Так как производная от алгебраической суммы равна той же сумме производных от слагаемых, то:

(¹/₃ х³ — х² — 3x + 5)' = (¹/₃ х³)'  — (х²)'  — (3x)'  + (5)'  = х² — 2х — 3.

Чтобы судить теперь, при каких значениях х данная функция возрастает или убывает, надо (§ 335) узнать, при каких значениях х производная положительна и при каких отрицательна, т. е., другими словами, надо решить 2 неравенства;

х² — 2х — 3 > 0 и х² — 2х — 3 < 0.

Для их решения мы. предварительно разложим трехчлен х² — 2х — 3  на множители, для чего найдем корни этого трехчлена:

х² — 2х — 3 = 0;      х = 1 ±√1²+ 3 = 1 ± 2;
x₁  = 3    х₂  = — 1.

Теперь выполним разложение {ч. I,отдел 9 глава 2 § 221):

х² — 2х — 3 = (x — 3) [x — ( — 1)].

Следовательно, неравенства можно написать так:

(x — 3) [x — ( — 1)] ^>_<  0.

Произведение двух сомножителей тогда положительно, когда   оба сомножителя положительны или когда оба отрицательны. Первое будет иметь место тогда, когда х больше большего из двух корней, т. е. когда x >3 (тогда и подавно. x > — 1), второе тогда, когда x меньше меньшего корня, т. е. когда x < —1 (тогда и подавно x < 3). Значит, в этих двух случаях производная положительна.  Если же один из двух сомножителей положительный, а другой отрицательный, то произведение отрицательно. Это может быть только тогда, когда значение х заключается между меньшим и большим корнем трехчлена, т. е. когда 3 > x >— 1.

Следовательно, при изменении х

и поэтому (§ 336):

f(x) возрастает |   f(x)  убывает   |    f(x)  возрастает.

Отсюда видно, что при переходе х через — 1 данная функция получает maximum а при переходе через + 3 она получает minimum. Значения эти равны:

maximum (при х = — 1) = — ¹/₃ —1 + 3 + 5 = 6²/₃;
minimum   (при х =  + 3)  =   9 — 9 — 9 + 5   =  — 4

Для более подробного представления о ходе изменения данной функции составим таблицу ее частных значений, например, такую:

Нанеся все эти значения на чертеж в виде отдельных точек и обведя эти точки непрерывною кривою, мы получим следующий график данной функции (черт.21):

Но   можно   воспользоваться признаками  возрастания или  убывания функции (§ 335): найти производную от f'(x) (иначе сказать, найти вторую производную от    f (х) и определить, когда она положительна и когда отрицательна.

Производная от функции f '(х) = х² — 2х — 3   будет f'' (x) = 2x —  2 = 2(x—1).

Очевидно, что при x > 1 она положительна, а  при   x <1 отрицательна.Значит, при   x > 1   производная  f'(x)   возрастает,   а при x < 1 она убывает. Следовательно, для всех значений x > 1   вогнутость кривой направлена вверх, а   при   всех   значениях x < 1    она    направлена вниз (таким образом, точка с абсциссой 1 есть точка перегиба). Это и подтвержается на нашем чертеже.

346. Пример 2-й.   f(x) = х³— 12х² + 48x — l3;

f '(x) = 3х² — 24х + 48 = 3 (х² — 8х + 16) = 3 (х — 4)².

Так как произведение 3 (х — 4)² при всяком значении х есть число положительное (кроме значения х = 4, когда оно равно нулю), то данная функция при изменении х от — ∞ до + ∞ постоянно возрастает и потому она не имеет ни maximum, ни minimum. При х = 4 производная равна нулю; это значит, что касательная, проведенная через точку с абсциссой 4, параллельна оси x-ов. Но касательная может быть параллельной оси x-ов только в трех случаях: когда кривая в точке касания или имеет maximum, или имеет minimum, или перегибается в этой точке. Наша кривая не имеет совсем ни maximum, ни minimum, значит, точка с абсциссой 4 есть точка перегиба.

Мы можем в этом убедиться еще иначе, если определим, для каких значений х кривая вогнута, и для каких —выпукла. Для этой цели можно было бы воспользоваться второю производного, но в данном примере благодаря особому виду первой производной:   f '(x) = 3 (х — 4)²  мы можем сразу определить, при каких значениях х эта производная возрастает и при каких — убывает. Очевидно, что при изменении х от 4 до + ∞ разность х — 4 возрастает от 0 до + ∞; следовательно, при этом возрастает и f '(х) от 0 до   + ∞ При изменении х от — ∞ до 4, разность х — 4 возрастает от — ∞ до 0; следовательно, квадрат этой разности(х — 4)²  при этом изменяется от + ∞ до 0; значит, f '(x) убывает от + ∞ до 0. Таким образом, для всех значений х, меньших 4, вогнутость кривой направлена вниз, а для всех значений х, больших 4, она направлена вверх, и потому точка с абсциссой 4 есть точка перегиба.

Для изображения графика данной функции составим предварительно таблицу частных значений:

Так как f(x) выражается числами с очень большой абсолютной величиной, то для удобства чертежа можно уменьшить все их в 10 раз (конечно, от этого чертеж окажется сжатым в вертикальном направлении в 10 раз). Предлагаем читателям самим исполнить этот чертеж.

347. Графическое решение кубичного уравнения вида х³ + рx + q  = 0. Графическим способом можно решить кубичное уравнение так же, как решается квадратное уравнение (ч. I, отдел 9 глава 2 § 226), а именно: перенеся все члены уравнения в левую часть, строят график функции 3-й степени, стоящей в левой части уравнения, и затем на чертеже находят величины абсцисс точек, в которых этот график пересекается с осью х-ов. Так, из чертежа 21 видно, что уравнение ¹/₃ х³ — х² — 3x + 5 = 0 имеет 3 корня, один отрицательный и 2 положительных, приблизительные величины которых можно найти на чертеже, изготовленном на миллиметровой бумаге.

Более удобен следующий способ, применяемый тогда, когда кубичное уравнение имеет вид:  х³ + рx + q  = 0   (в  нем  недостает члена с  х²) К такому виду можно  привести уравнение х³ + aх ² +bx + c  = 0, если введем вспомогательное неизвестное у, связанное с х равенством: х = y   — ^a/₃ .

Пусть, например, требуется решить уравнение х³ — 3 х— 2 = 0. Для этого, представив уравнение в виде х³ = 3 х + 2, построим графики двух функций у₁ = х³ и  у₂ = 3 х + 2 и затем определим абсциссы точек пересечения этих, двух графиков. (черт. 22).

Глава седьмая.

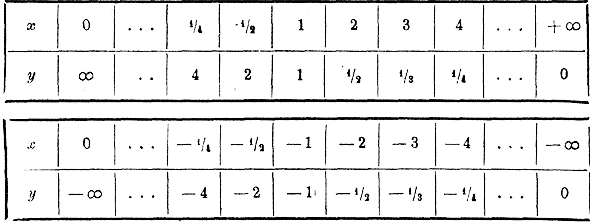
Функция вида    у =  ^a/_x 

348. Особенности этой функции.  Функция   у =  ^a/_x, в которой а постоянное число, выражает, как мы видели (ч. 1, отдел 2 глава 8 §105), обратную пропорциональную зависимость между переменными числами и х. Когда мы говорили о графическом изображении этой зависимости (ч. I, отдел 3 глава 2 § 112), мы тогда строили график этой функции, но только для положительных значений х. Теперь мы построим кривую, выражающую функцию  у =  ^a/_x не только для положительных, но и для отрицательных значений х, и кроме того рассмотрим некоторые особенности этой функции.

Возьмем случай, когда а = 1, т. е. когда функция имеет вид у =  ¹/_x. Очевидно, что при всяком значении х, отличном от нуля (как положительном, так и отрицательном), функция эта возможна и получает единственное значение, причем для положительных значений х она положительна, а для отрицательных  значений   х — отрицательна.  При  х = 0 функция   ¹/_xперестает существовать (деление на 0 невозможно), но если число х не равно 0, а только приближается к 0, оставаясь положительным (например, если х переходит через значения: 0,1; 0,01; 0,001; и т. д.), то функция возрастает неограниченно (она делается равной 10, 100, 1000 и т. д.), иначе сказать, она стремится к + ∞. Если же х приближается к  0, оставаясь отрицательным   (например,   если х переходит через значения — 0,1;— 0,01; —0,001; и т. д.), то функция — стремится к — ∞ (переходя через значения —10,— 100, —1000 и т. д.). С другой стороны, если х—>+ ∞ или если х—> —  ∞, функция и в том и в другом случае стремится к 0. Таким образом,

Таким образом, при переходе х через нулевое значение от отрицательных значений к положительным функция сразу переходит от — ∞ к +∞. При всех же значениях х, неравных нулю, функция изменяется непрерывно, т. е. бесконечно малому приращению числа х соответствует и бесконечно малое приращение функции   у = ¹/_x. Действительно, если дадим  числу х какое-нибудь приращение h, то функция получит приращение k, равное

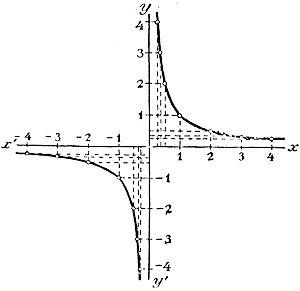
Если h —> 0, то числитель полученной дроби стремится к нулю а знаменатель к х² , т. е. к числу, не равному нулю (если только х не равен нулю); значит, правая часть полученного нами равенства (следовательно, и его левая часть) стремится к 0, когда h —> 0. Из этого следует, что при непрерывном изменении числа х, если только х не переходит через нулевое значение, функция  у = ¹/_x изменяется тоже непрерывно; при переходе же х через  нуль  функция  претерпевает  разрыв   непрерывности, переходя скачком от — ∞ к + ∞.

Заметив все это, построим теперь график нашей функции при помощи, например, таких таблиц частных значений:

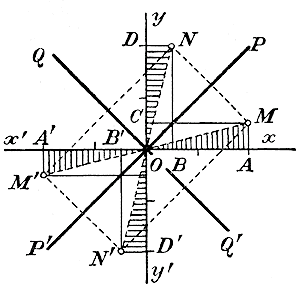
Равным образом, ветвь кривой, лежащая в угле х'Оу', по мере продолжения ее налево, неограниченно приближается к полуоси Ох', никогда ее не достигая. При неограниченном уменьшении положительного значения х ветвь кривой в угле хОу приближается все более и более к полуоси Оу, никогда ее однако не достигая (так как  дробь¹/_x  при x = 0   перестает существовать);   также при неограниченном уменьшении абсолютной величины отрицательного значения х ветвь кривой в угле х'Оу' все более и более приближается к полуоси Оу'никогда ее не достигая.

Прямая, к которой кривая неограниченно приближается, никогда ее однако не достигая,называется асимптотой. Гипербола имеет 2 асимптоты: ось x-ов и ось y-ов.

2. Оси   симметрии.   Центр   симметрии.   Уравнение  у = ¹/_x можно написать так:    ху = 1.   Из этого вида   замечаем, что переменные х и у играют в уравнении одинаковую роль, т. е. если мы заменим у на х, а х на у, то уравнение от этого не изменится (такие уравнения называются симметричными). Поэтому если мы нашли, что такому уравнению удовлетворяет какая-нибудь пара значений: х = а и у = b, то ему же удовлетворяет и другая пара значений: х = b, у = а, составленная из первой пары заменою х на у, и наоборот. Например, как видно из таблицы значений, приведенной выше, на гиперболе лежат точки (¹/₂, 2) и (2, ¹/₂). Уравнение ху = 1 также не изменяется, если мы вместо х возьмем — х и вместо y возьмем — у. Значит, если на гиперболе имеется точка (а, b), то на ней же (на другой ветви) должна находиться и точка (—а,— b). Например, из той же таблицы видно, что на гиперболе лежат  точки (¹/₂, 2) и (— ¹/₂ — 2), или точки (3, ¹/₃ ) и (— 3, —¹/₃ ). Заметив это, возьмем такие 4 точки (черт. 24).

М  (2, ¹/₂),    N  (¹/₂, 2),   М '  (— 2 — ¹/₂) ,  N '  (— ¹/₂ — 2).

Из чертежа легко усмотреть, что эти., биссектрисы делят пополам 4 угла указанных равнобедренных треугольников, лежащие при общей вершине О, и потому они делят пополам основания этих треугольников и перпендикулярны к ним. Отсюда следует, что точки M и N, а также и точки M' и N', симметрично расположены относительно прямой PP' а точки M и N', а также и точки N и    M', симметрично лежат относительно прямой QQ'. Так как сказанное о 4 точках M, N, М' и N' может быть повторено о всяких других 4 точках, расположенных подобным же образом на гиперболе, то заключаем, что гипербола имеет 2 оси симметрии, именно биссектрисы прямых углов, образуемых осями координат. Пересечение этих осей, т. е. точка О, служит центром симметрии, так как прямые ММ' и NN' делятся этою точкою пополам.

Предположим  теперь,  что  в  функции  у = ^a/_x число  а   не равно 1, а есть какое-нибудь положительное число, большее или меньшее 1. Тогда она выразится такою же гиперболою, как и функция  ¹/_x, только абсолютные величины ординат ее будут больше (если а >1), или меньше (если a < 1) соответствующих ординат гиперболы — в одном и том же отношении а : 1 (ч. I, черт., § 112)

Если а будет   число  отрицательное  (например,  у = — ¹/_x), то положительным значениям х будут соответствовать отрицательные значения у, и наоборот. Значит, ветви гиперболы будут расположены в углах х'Оу и хОу', свойства же кривых останутся те же самые, как и для положительных значений числа а.

349. Производная от функции у = ^a/_x .

Сначала найдем  производную от функции  у = ¹/_x. Для этого дадим  числу х какое-нибудь приращение h.   Тогда у получит приращение k, равное

Для функции у = ^a/_x производная будет (§ 332):

Применения. Воспользуемся производной для суждения о возрастании и убывании функции, а также и вогнутости и выпуклости кривой.

Производная от функции у = ¹/_x, равная   при   всяком значении х, кaк положительном, так и отрицательном, всегда отрицательна (при х = 0 она не существует). Поэтому (§ 335) при возрастании х от  — ∞ до + ∞ функция ¹/_x постоянно   убывает (при      х = 0, она как мы видели, претерпевает разрыв непрерывности). Значит, функция не имеет ни maximum ни minimum.

При возрастании числа х от — ∞ до 0, число  х²  убывает; значит,  дробь при этом возрастает, а дробь убывает. Это показывает (§ 336), что в угле х'Оу' вогнутость гиперболы направлена вниз.  При возрастании   х от 0 до+ ∞, число х² возрастает, дробь , убывает,  а  дробь возрастает.   Это означает, что в угле хОу вогнутость гиперболы направлена вверх. Это и подтверждается чертежом 23.