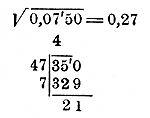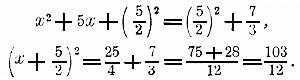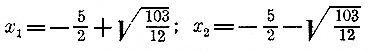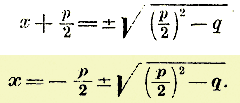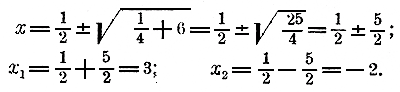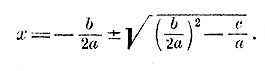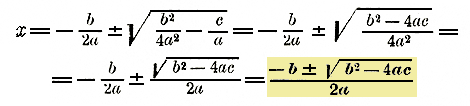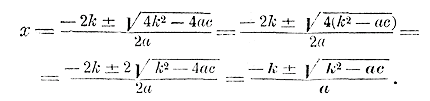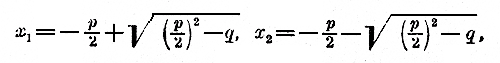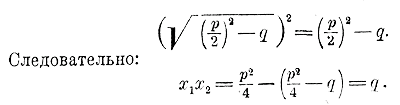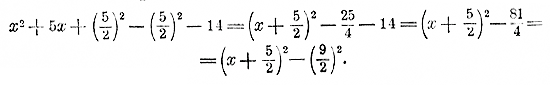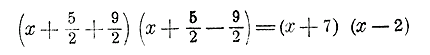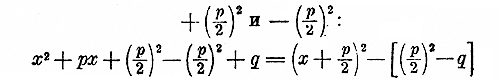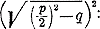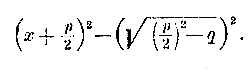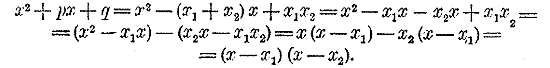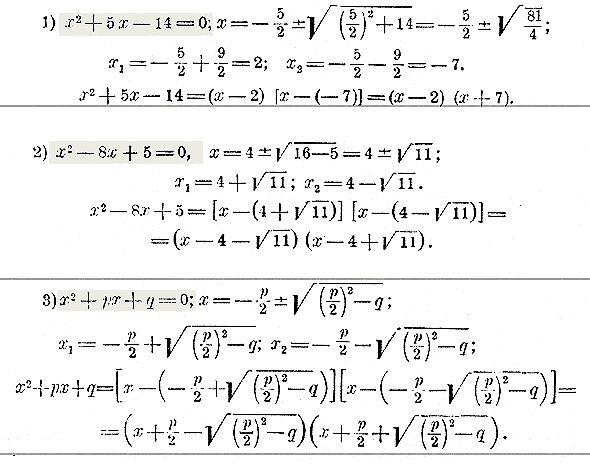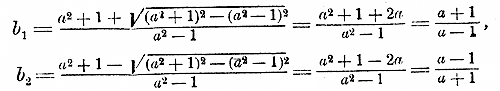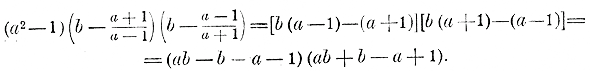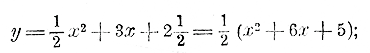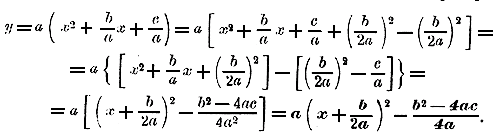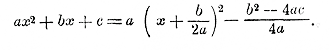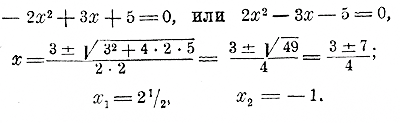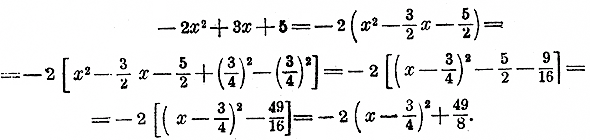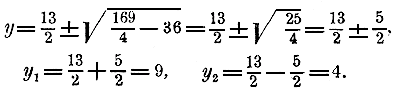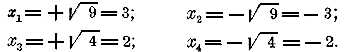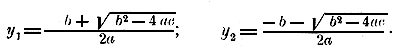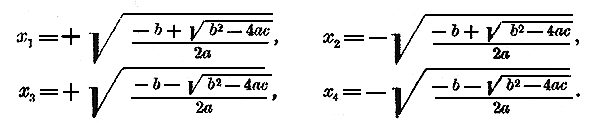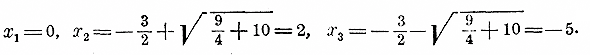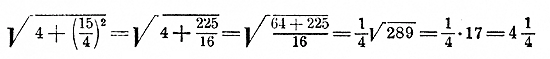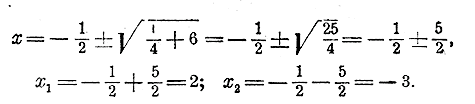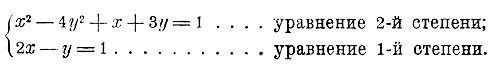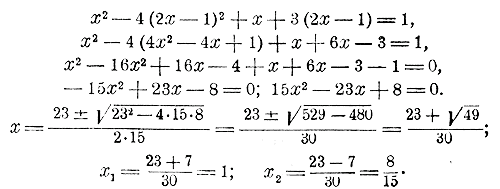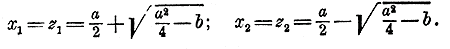| АЛГЕБРА В НАЧАЛО |
|
ОТДЕЛ ДЕВЯТЫЙ. НЕКОТОРЫЕ УРАВНЕНИЯ СТЕПЕНИ ВЫШЕ ПЕРВОЙ. Глава первая. Квадратное уравнение. Квадратное уравнение. 208. Задача. Моторная лодка спустилась по течению реки на расстояние 28 км и тотчас же вернулась назад; на это ей потребовалось 7 часов. Найти скорость движения лодки в стоячей воде, если известно, что вода в реке движется со скоростью 3 км в час. Пусть скорость движения лодки в стоячей воде будет х км в час; тогда по течению реки она двигалась со скоростью (х + 3) км в час, а против течения со скоростью (х —3) км в час. Следовательно, 28 км лодка прошла в 28/(х + 3) часов, когда двигалась по течению, и в 28/(х —3) часов, когда возвращалась назад. Согласно условию задачи мы имеем уравнение:
Освободив от знаменателей, получим: 28 (х —3) + 28 (х + 3) = 7 (х + 3) (х —3), т. е. 28x — 84 + 28x + 84 = 7 (x2 — 9) = 7x2 — 63, или 56x =7x2— 63. Мы получили уравнение, в котором есть член, содержащий неизвестное во второй степени, но нет членов, содержащих неизвестное в более высоких степенях. Такое уравнение называется уравнением второй степени, или квадратным. Как можно решать такие уравнения, мы увидим в этой главе. 209. Нормальный вид квадратного уравнения. В квадратном уравнении (а также и в уравнениях более высоких степеней) принято, после упрощения уравнения, переносить все его члены в одну левую часть, так что правая часть уравнения делается равной нулю. Так, уравнение, составленное нами для решения предыдущей задачи, после указанного перенесения членов будет: 56x— 7x2 + 63 = 0, или после расположения членов по убывающим степеням буквы х: — 7x2 + 56x + 63 = 0 Числа —7, +56 и +63 называются коэффициентами этого квадратного уравнения; из них число +63 называется свободным членом, а числа —7 и +56 первым и вторым коэффициентами (мы предполагаем, что члены уравнения всегда расположены по убывающим степеням буквы х). Числа эти могут быть и положительные, и отрицательные, и даже нули (кроме первого коэффициента, который не может быть нулем, так как в противном случае уравнение не было бы квадратным). Если ни один из трех коэффициентов не равен нулю, то уравнение называется полным. Общий вид такого уравнения (нормальный вид) есть следующий: ax2 + bx + c = 0 Заметим, что первый коэффициент а мы можем всегда сделать положительным, переменив в случае надобности перед всеми членами знаки на противоположные (другими словами, умножив обе части уравнения на —1). Так, приведенное выше уравнение мы можем написать так. 7x2 — 56x — 63 = 0 210. Решение неполных квадратных уравнений. Квадратное уравнение называется неполным, когда в нем нет члена, содержащего х в первой степени, или нет свободного члена; другими словами, когда второй коэффициент b равен нулю, или когда свободный член с равен 0. В первом случае уравнение имеет вид ax2+ c = 0, во втором ax2 + bx = 0 (может даже случиться, что одновременно и b = 0 и с = 0; тогда уравнение будет вида ax2 = 0). Рассмотрим решение всех этих неполных уравнений. I. Неполное квадратное уравнение вида ax2 + c = 0. Возьмем три следующих примера: а) 3x2 — 27 = 0 . Перенеся свободный член направо, получим: 3x2 = 27 , и, следовательно, x2 = 27/3 = 9. Значит, х есть квадратный корень из 9, т. е. число + 3 или число —3. Условимся знаком √ обозначать арифметическое значение корня; тогда мы можем написать: x = ± √9 = ± 3. Таким образом, данное уравнение имеет два решения. Обозначая одно из них x1 а другое х2, мы можем эти решения написать так: x1 = + √9 = + 3; х2 = — √9 = — 3. б) 2x2 — 0,15 = 0. Перенеся свободный член, получим: 2x2 = 0,15 и x2 = 0,075. Значит: x = ±√0,075 . Найдем √0,075 с точностью, положим, до 1/100 ( отдел7 глава 1 § 171):
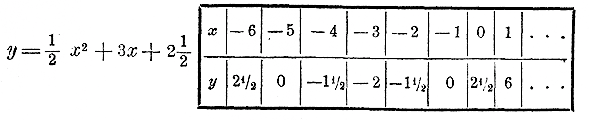
Следовательно, x1 = 0,27..., х2 = — 0,27... в) 2x2 + 50 = 0. Перенеся 50 направо, получим: 2x2 = — 50; x2 = — 50/2 = — 25; х = ±√—25 Так как из отрицательного числа нельзя извлечь квадратного корня, то данное уравнение не имеет решений (вещественных). Таким образом, неполное квадратное уравнение вида ax2 + c = 0 вообще решается так: ax2 = — с; x2 = — с/a, Если выражение — с/a есть число положительное, то из него можно извлечь квадратный корень (точно или приближенно), и тогда для х получаем два значения с одинаковою абсолютною, величиною, но одно положительное, другое отрицательное. Если же выражение — с/a есть число отрицательноe, то уравнение не имеет вещественных корней. II. Неполное квадратное уравнение вида ax2 + bx = 0 . Как частный пример возьмем уравнение 2x2 — 7x = 0. В левой части этого уравнения вынесем х множителем за скобки: х(2х — 7) = 0. Теперь левая часть уравнения есть произведение, а правая равна нулю. Но произведение равняется нулю только тогда, когда какой-нибудь из сомножителей равен нулю; поэтому наше уравнение удовлетворяется только тогда, когда первый сомножитель х равен нулю или когда второй сомножитель 2х — 7 равен нулю (и когда, следовательно, x = 7/2) Значит, данное уравнение имеет два решения: x1 = 0 и х2 = 7/2 = 3 1/2 Таким образом, неполное квадратное уравнение вида ax2 + bx = 0 решается вообще так. ax2 + bx = 0; х (ах + b) = 0; x1 = 0 ; ax2 + b = 0 ; x2 = — b/a 211. Двучлен второй степени. Если в неполных квадратных уравнениях возьмем левую часть независимо от правой, то получим выражение: ax2+ c или ax2 + bx Выражения эти называются двучленами второй степени относительно х. В них буква х означает переменное , число, могущее принимать какие угодно значения, а буквы а, b и с означают какие-нибудь постоянные числа, как положительные, так и отрицательные; таковы, например, выражения: 3x2— 27, 2x2— 0,15, 2x2 + 50, x2 — 8x, 2x2 — 7x,... и т.п. Конечно, численная величина двучлена зависит от того значения, которое мы будем придавать переменному числу х ; напр., двучлен 3x2— 27 при х = 0 будет — 27, при х = 1 он будет —24, при х = 2 он окажется 3 • 22 — 27 = 12 — 27 = —15, при х = 5 получим 3 • 52 — 27 = 75 — 27 = 48... и т. п. Таким образом, двучлен 2-й степени от х представляет собою некоторую функцию от х; Заметим, что между двучленом 2-й степени и левою частью неполного квадратного уравнения та существенная разница, что буква х в уравнении означает только то число, при котором двучлен, стоящий в левой части уравнения, равен нулю, тогда как в двучлене, взятом независимо от уравнения, буква х означает всякие числа, и, следовательно, двучлен может получать разнообразные значения. То число, которое, будучи подставлено в двучлен на место х, обращает этот двучлен в нуль, называется корнем двучлена; значит, корень двучлена есть в то же время и корень того неполного квадратного уравнения, которое получится, если этот двучлен приравняем нулю. 212. График двучлена второй степени. Чтобы наглядно представить себе, как изменяется двучлен 2-й степени при изменении переменного числа х, мы построим его график так же, как прежде мы строили график двучлена 1-й степени ( отдел 3 глава 3 § 115), или график функции у = ax2 (т. е. график одночлена 2-й степени, отдел 6 глава 3 § 159). Рассмотрим совместно следующие три функции: 1) у = 1/2 x2 ; 2) у = 1/2 x2 + 1 ; 3) у = 1/2 x2 — 11/2 ; Составим таблицу их частных значений, напр., такую:
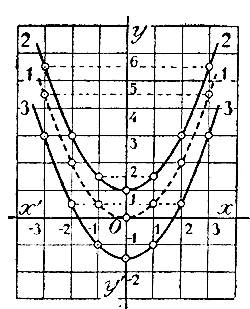
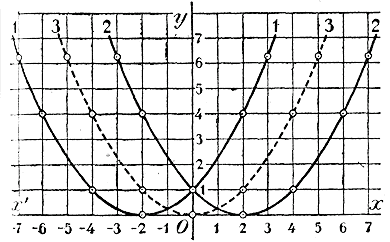
Теперь, при помощи координатных осей и произвольной единицы длины, нанесем все эти значения на чертеж в виде точек и через полученные точки проведем кривые линии.
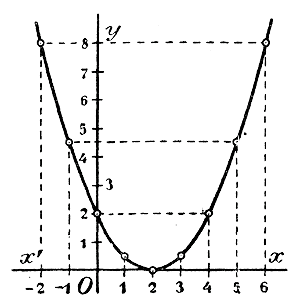
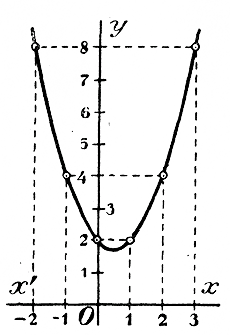
Черт. 1 Первая из этих линий (прерывистая линия) есть парабола, которую мы чертили раньше (отдел 6 глава 3 § 158); она проходит через начали координат. Кривые 2-я и 3-я через точку О не проходят. Сравнивая все три кривые между собою, замечаем, что при одной и той же абсциссе х ордината 2-й кривой больше на 1, а ординaта 3-й кривой меньше на 11/2 единицы, сравнительно о ординатой параболы 1-й. Поэтому можно сказать, что 2-я кривая есть та же парабола 1-я, только перемещенная параллельным перенесением1) на одну единицу вверх, а 3-я кривая есть парабола 1-я, перемещенная параллельным перенесением на 11/2 единицы вниз. Вообще кривая, выражающая функцию у = ax2+ c, есть парабола у = ax2 перемещенная параллельным перенесением на с единиц вверх, если с >0, и вниз, если с < 0. Ветви этой параболы направлены вверх, когда коэффициент при х есть число положительное (как в наших примерах), и вниз, когда этот коэффициент есть число отрицательное. В первом случае функция имеет наименьшее значение, во втором случае — наибольшее; и то и другое имеет место при х = 0 и равно свободному числу с. Изобразим еще график двучлена у = 1/2 x2 — x составляющего частный случай двучлена вида у = ax2 + bx .
Черт.2 Особенность этой кривой состоит в том, что она проходит через точку (0,0), т. е. через начало координат. 213. Корни неполных квадратных уравнений в графическом изображении. Из трех парабол, изображенных нами на черт. 1, одна (3-я) пересекается с осью x-ов в двух точках. Так как в этих точках ординаты равны нулю, и они выражают значения данного двучлена, то, значит, абсциссы точек пересечения будут корни уравнения 1/2 x2 — 11/2 = 0. На нашем чертеже мы можем только усмотреть, что эти корни одинаковы по абсолютной величине, но противоположны по знаку, и что абсолютная величина каждого корня превосходит 11/2, единицы. Если бы мы исполнили чертеж возможно точнее (напр, на миллиметровой бумаге, взяв за единицу длины сантиметр), то на чертеже мы могли бы точнее найти величину корней (приблизительно они равны ±. 1,7). Парабола 2-я не пересекается с осьюx-ов. Значит, уравнение 1/2 x2 + 1 = 0 не имеет корней. Из черт.2 видно, что уравнение 1/2 x2 — x = 0 имеет два корня, из которых один есть 0. 214. Примеры решения полных квадратных уравнений. Для первого примера возьмем то квадратное уравнение, которое было составлено для задачи § 208: 7x2 — 56x — 63 = 0. Разделим все его члены на 7 и перенесем свободный член направо: x2 — 8х = 9. Зададимся теперь вопросом, нельзя ли к двучлену x2 — 8х приложить такой третий член, чтобы образовался трехчлен, представляющий собою полный квадрат. Мы легко ответим на этот вопрос, если изобразим двучлен так: x2 — 2х • 4. Теперь ясно, что если этот двучлен дополним членом 42, то получим трехчлен x2 — 2х • 4 + 42, равный квадрату разности x — 4. Но если к левой части уравнения мы добавим число 42 (т. е. 16), то и к правой части должны добавить то же самое число. Сделав это, получим: x2 — 8х + 16 = 9 + 16 , т. е. (x— 4)2 = 25. Таким образом, разность x — 4 есть такое число, квадрат которого равен 25; значит, эта разность должна равняться квадратному корню из 25, т. е. числу 5 или числу — 5: x — 4 = + √25 = + 5 или x — 4 = — √25 = — 5. Перенеся теперь член — 4 в правую часть, найдем два решения: x1 = 4 + 5 = 9 и х2 = 4 — 5 = — 1. Оба эти решения годны для данного уравнения (в чем можно убедиться поверкою), но для задачи, из которой выведено уравнение, отрицательное решение — 1 не годится, так как в задаче отыскивается абсолютная величина скорости, а не ее направление. Для второго примера возьмем уравнение . 3x2 + 15x — 7 = 0. Разделим все члены на 3 и перенесем свободный член направо: „ x2 + 5x = 7/3 Из двучлена x2 + 5x можно сделать квадрат суммы, если добавим к нему трeтий член (5/2 )2. Приложив этот член к обеим частям уравнения, получим:
Отсюда видно, что
Вычислим 103/12 с точностью, положим, до1/10 :
Следовательно: x1 = — 2,5 + 2,9 ... = 0,4 и х2 = — 2,5 — 2,9 .. . = — 5,4... 215. Формула корней приведенного квадратного уравнения. Квадратное уравнение, у которого первый коэффициент есть +1, называется приведенным уравнением. К такому виду, как мы видели сейчас на примерах, уравнение может быть приведено и в том случае, когда первый коэффициент не 1; стоит только все члены уравнения разделить на этот коэффициент. В общем виде приведенное уравнение обыкновенно изображается так: x2 + px + q = 0. Решим это буквенное уравнение, проделав над ним те же преобразования, которые были указаны на частных примерах. Перенесем свободный член в правую часть: x2 + px = — q Так как px = 2х • p/2 , то, желая обратить двучлен x2+ px в полный квадрат, прибавим к обеим частям уравнения по (p/2)2 : x2 + px + (p/2)2 = — q + (p/2)2 Теперь уравнение можно представить так: ( x + p/2)2 = (p/2)2 — q откуда находим:
Формулу эту можно высказать так: неизвестное приведенного квадратного уравнения равно половине второю коэффициента, взятого с противоположным знаком, плюс-минус корень квадратный из квадрата этой половины без свободного члена. Формулу эту надо запомнить и в буквенном выражении и в словесном. Примеры. 1) x2 — x — 6 = 0. Чтобы уравнение это уподобить буквенному x2 + px + q = 0, представим его так: x2 + ( —1) x + ( — 6) = 0. Теперь видно, что в этом примере р =—1 и q = — 6; поэтому:
Поверка: 32 — 3 — 6 = 0; (—2)2 — (—2) —6 = 0. 2) x2 —18 x + 81 = 0; здесь р= — 18, q = + 81; поэтому: х = 9 ±√81 —81 = 9 ± 0 = 9. Уравнение имеет только один корень. 3) x2 —2 x + 5 = 0 ; х = 1 ±√1 —5 = 1 ±√ — 4 . Корни мнимые. Из этих примеров мы видим, что если (p/2)2 — q > 0, то уравнение имеет 2 различных решения; если (p/2)2 — q = 0, то урав-нение имеет одно решение; наконец, если (p/2)2 — q < 0, то уравнение не имеет вовсе решений (вещественных). 216. Общая формула корней квадратного уравнения. Уравнение ax2 + bx + c = 0 по разделении его членов на а приводится к приведенному уравнению: x2 + b/a x + c/a = 0 Решив это уравнение по формуле приведенного уравнения, найдем:
Выражение это можно упростить так:
В этом упрощенном виде формулу полезно запомнить, ее можно высказать так: неизвестное полного квадратного уравнения равно дроби, у которой числитель есть второй коэффициент, взятый с противоположным знаком, плюс-минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент2). Эту формулу можно назвать о б щ е ю, так как она годится и для приведенного уравнения (если положим а =1) и для неполных квадратных уравнений (если положим b = 0 или с = 0). Из общей формулы видно, что если b2— 4ас > 0, то уравнение имеет 2 различных решения; если b2— 4ас = 0, то уравнение имеет одно решение, именно — b/2a; если же b2— 4ас < 0, то уравнение не имеет ни одного решения (оба решения мнимые). Так, уравнение 3x2 + 5x — 6 = 0 имеет 2 решения, так как уравнение 9x2 — 6x + 1 = 0 имеет одно решение, так как уравнение 3x2 — 5x + 6 = 0 не имеет решений (вещественных), так как 217. Упрощение формулы, когда b четное число. Общая формула упрощается, если b четное число. Так, положив b = 2k, найдем:
Эта формула отличается от общей отсутствием цифровых множителей 4 и 2. 218. Число корней квадратного уравнения. Мы видели, что квадратное уравнение имеет иногда два корня, иногда один, иногда ни одного (случай мнимых корней). Однако согласились приписывать квадратным уравнениям во всех случаях два корня, разумея при этом, что корни могут быть иногда равными, иногда мнимыми. Причина такого соглашения состоит в том, что формулы, выражающие мнимые корни, обладают теми же свойствами, какие принадлежат вещественным корням, cтоит только, совершая действие над мнимыми числами, руководиться правилами, выведенными для вещественных чисел, принимая притом, что (√—a)2 = — а. Точно также, когда уравнение имеет один корень, мы можем, рассматривая этот корень как два одинаковых, приписать им те же свойства, какие принадлежат разным корням уравнения. Два из этих свойств мы сейчас укажем. 219. Два свойства корней квадратного уравнения. Если сложим две формулы, выражающие корни приведенного квадратного уравнения x2 + px + q = 0 :
то радикалы взаимно уничтожатся, и мы получим: x 1 + х2 = — p/2 — p/2 = — p Если же две формулы перемножим, то получим (произведение суммы двух чисел на их разность равно разности квадратов этих чисел):
Каково бы ни было подкоренное число (p/2)2 — q всегда
Таким образом, сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Следствия. 1) Пользуясь этими свойствами, мы легко можем составить квадратное уравнение, у которого корнями были бы данные чиcла. Пусть, напр., надо составить уравнение, у которого корни были бы числа 2 и 3; тогда из равенств 2 + 3 = — р и 2•3 = q находим: р = — 5 и q = 6; следовательно, уравнение будет: x2 — 5x + 6 = 0. Подобно этому найдем, что 3 и — 7 будут корни уравнения x2 — [3 + ( — 7)] х + 3 ( — 7) = 0, т. е. x2 + 4x — 21 = 0; числа 3 и 0 будут корни уравнения x2 — 3x = 0, и т. п. 2) При помощи тех же свойств мы можем, не решая квадратного уравнения, определить знаки его корней, если эти корни вещественные. Пусть, напр., имеем уравнение x2 + 8x + 12 = 0 Так как в этом примере выражение (p/2)2 — q , т. е. 42 — 12, есть число положительное, то оба корня вещественные. Обращая внимание на свободный член, видим, что он имеет знак + ; значит, произведение корней должно быть положительное число, т. е. оба корня имеют одинаковые знаки. Эти знаки должны быть минусы, так как сумма корней отрицательна (она равна —8). Уравнение x2 + 8x — 12 = 0 имеет корни с разными знаками (потому что их произведение отрицательно), причем отрицательный корень имеет большую абсолютную величину (потому что их сумма отрицательна), и т. п. 3) Так как корни уравнения ax2 + bx + c = 0 те же самые, что и корни уравнения Трехчлен 2-й степени и его графическое изображение. 220. Трехчлен 2-й степени. Выражение вида ax2 + bx + c, в котором коэффициенты а, b, с означают какие угодно постоянные числа, а х — переменное число, называется трехчленом второй степени (относительно переменного х). Те значения х, при которых трехчлен обращается в нуль, называют его нулевыми значениями или корнями; конечно, эти корни те самые, которые принадлежат квадратному уравнению ax2 + bx + c = 0, или—что все равно — приведенному уравнению x2 + b/a x + c/a = 0 В частном случае при а =1 трехчлен принимает вид x2 + px + q при b = 0 или при с = 0 трехчлен обращается в двучлен ax2 + c или ax2 + bx. В этой главе мы рассмотрим некоторые свойства трехчлена и процесс его изменения при изменении числа х. 221. Разложение трехчлена x2 + px + q на множители 1-й степени относительно х. Покажем два способа такого разложения. 1-й способ: посредством введения двух вспомогательных членов. Пусть требуется, разложить трехчлен x2 + 5x —14. Обращая внимание на первые два члена, замечаем, что если к ним добавить третий член, равный квадрату половины коэффициента при втором члене, т. е. член (5/2)2 то из них составится трехчлен, равный (x + 5/2)2. Заметив это, приложим к данному трехчлену два взаимно уничтожающихся члена: + (5/2)2 и — (5/2)2, от чего, конечно, трехчлен не изменится. Тогда получим:
Мы привели данный трехчлен к такому виду, при котором он представляет собою разность двух квадратов; а такую разность можно разложить на два множителя: на сумму возвышаемых чисел и на их разность. Сделав такое разложение, получим:
Пусть еще требуется разложить трехчлен x2 — 8x + 5. Прибавим два вспомогательных члена + 42 и — 42 : x2 — 8x + 42 — 42+ 5 Первые три члена составляют (x— 4)2 последние 2 члена дают число —11: (x— 4)2 — 11. Вместо 11 можно подставить (√11 )2: (x— 4)2 — (√11 )2 Теперь эта разность квадратов разлагается так: (x — 4 + √11 ) (x— 4 + √11 ). Если вычислим 11 с точностью, положим, до 1/1000, то найдем: √11 = 3,316... Подставив, получим: (x — 0,683 .. .) (x —7,316...). Этот прием можно применить и к буквенному трехчлену x2 + px + q , а именно: введем два вспомогательных члена
Вместо разности (p/2)2 — q мы можем подставить выражение
Эту разность квадратов разлагаем на 2 множителя:
2-й способ: посредством предварительного нахождения корней трехчлена. Найдем корни трехчлена, решив квадратное уравнение: x2 + px + q = 0 . Пусть эти корни будут x1и х2. Тогда, как мы видели (§ 219): x1+ х2 = — р и x1 х2 = q. Из этих равенств находим: р = — (x1+ х2) и q = x1 х2. Подставим в трехчлен на место р и q эти выражения и затем преобразуем полученный многочлен:
Мы видим таким образом, что трёхчлен x2 + px + q разлагается на два множителя, из которых первый равен разности между х и одним корнем трехчлена, а второй равен разности между х и другим корнем трехчлена. Применив этот способ к примерам, разобранным сейчас первым способом, мы придем к тем же разложениям:
222. Разложение трехчлена ax2 + bx + c . Такой трехчлен прежде всего можно представить так: ax2 + bx + c = a ( x2 + b/a x + c/a ) Выражение, стоящее внутри скобок, есть трехчлен вида x2 + px + q. Его корни x1и х2 будут те же самые, что и трехчлена ax2 + bx + c. Найдя их, можем, по доказанному в предыдущем параграфе, разложить этот трехчлен так: x2 + b/a x + c/a = ( x — x1) (x— х2) Следовательно: ax2 + bx + c = a ( x — x1) (x— х2). Таким образом, разложение трехчлена ax2 + bx + c отличается от разложения трехчленx2 + px + q только дополнительным множителем а. Примеры. 1) Трехчлен 2x2 — 2x — 12, у которого корни 3 и — 2, можно разложить так 2 (х — 3) (х + 2). 2) (а2 — 1) (b2 +1) — 2b (а2 +1). Заметив, что данное выражение есть трехчлен второй степени относительно буквы b, расположим его по степеням этой буквы: (а2 — 1) b2 — 2(а2 +1) b + (а2 — 1). Корни этого трехчлена (принимая b за переменное число) будут (§ 217):
Следовательно, данный трехчлен представится так:
223. Следствие. По данным корням можно составить квадратное уравнение (иначе, чем это указано в § 219). Так, уравнение, имеющее корни 3 и — 2, будет х2 — х — 6 = 0. Конечно, все члены этого уравнения можно умножить на произвольное число, не зависящее от х (напр, на 2), от чего корни не изменятся. 224. График трехчлена второй степени. Сначала мы рассмотрим график такого трехчлена, который может быть представлен в виде произведения а( х + m)2. Напр., возьмем такие две функции: 1) y = 1/4 (x + 2)2 и 2) у= 1/4(х —2)2. Для сравнения мы изобразим на том же чертеже еще параболу: 3) y = 1/4 х2 Предварительно составим таблицу частных значений этих трех функций, напр, такую:
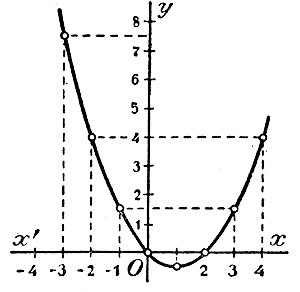
Нанеся все эти значения на чертеж, получим три графика, изображенные на черт. 3.
Черт 3. Рассматривая этот чертеж, мы замечаем, что кривая 1-я есть та же парабола 3-я, только перенесенная на 2 единицы влево, а кривая 2-я есть та же парабола 3-я, но перенесенная на 2 единицы вправо. Обобщая этот вывод, можем сказать, что график функции у =а( х + m)2 есть парабола, выражающая функцию у =ах2, только парабола эта перенесена влево, если m > 0, и вправо, если m < 0, на столько единиц, сколько их заключается в абсолютной величине числа m. Ветви этой параболы направлены вверх, если а >0 (как в наших примерах), и вниз, если a < 0 (напр., если бы было задано: y = — 1/4 (x + 2)2 . Теперь возьмем трехчлен вида: ax2 + bx + c , напр, такой частный случай:
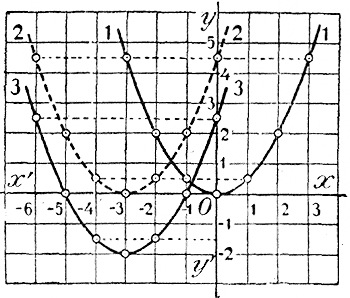
Построив точки, выражающие эти значения, и проведя через них кривую (кривая 3-я, черт. 4), мы получим искомый график.
Покажем теперь, что этот график есть та же парабола, которая выражает функцию во-первых, вынесем за скобки коэффициент при х2 во-вторых, к трехчлену, стоящему в скобках, добавим два взаимноуничтожающихся члена: + 32 и — 32 (как мы бы сделали, если бы хотели разложить этот трехчлен на множители способом введения двух вспомогательных членов): y = 1/2 ( х2 + 6x +5 + 32 — 32) и, в-третьих, сгруппируем члены многочлена в 2 группы так:
Принимая теперь во внимание примеры, разобранные в двух предыдущих параграфах, мы можем поступить так: Построим параболу, выражающую функцию: y = 1/2 х2 (кри-вая 1-я, черт. 4); затем перенесем ее на 3 единицы влево, Тогда получим 2-ю параболу, выражающую функцию y = 1/2 ( х + 3 )2. Эту параболу перенесем теперь на 2 единицы вниз; тогда получим третью параболу, выражающую данную функцию. Возьмем теперь трехчлен в общем виде: у = ax2 + bx + c и преобразуем его так, как было сейчас указано на частном примере:
Теперь мы можем утверждать, что график трехчлена у = ax2 + bx + c есть парабола у = ax2 , перемещенная двойным параллельным перенесением: во-первых, параллельно оси x-ов на столько единиц, сколько их есть в абсолютной величине числа b/2a, влево, если это число положительное, и вправо, если оно отрицательное; во-вторых, параллельно оси y-ов на столько единиц, сколько их есть в абсолютнои величине числа 225. Замечание. Когда в трехчлене коэффициент при x2 есть число положительное (как в примере предыдущего параграфа), тогда ветви параболы направлены вверх. Если же этот коэффициент число отрицательное, то ветви параболы должны быть направлены вниз. Так, если возьмем: y = — 1/2 х2 — 3x — 2 1/2, то, вынеся знак — за скобки, мы получим: y = — ( 1/2 х2 + 3x + 2 1/2). Сравнивая эту функцию с той, которую мы изобразили графически в предыдущем параграфе, мы замечаем, что при одинаковых значениях абециссы х ординаты нашей новой функции должны быть такие же по абсолютной величине, как и ординаты прежней функции, только противоположного направления. Значит, получится такая же парабола, как парабола 3-я черт. 4, но расположенная ветвями вниз, а вершиной вверх, симметрично с параболой 3-й этого чертежа. 226. Графическое решение полного квадратного уравнения. Квадратное уравнение можно графически решить таким способом. Построив на миллиметровой бумаге параболу, выражающую трехчлен, стоящий в левой части уравнения, находим точки пересечения этой параболы с осью х-ов (если такие точки существуют). Абсциссы этих точек и будут корни уравнения, так как при этих абсциссах ординаты, выражающие соответствующие значения трехчлена, равны нулю. Примеры. 1) 1/2 х2 + 3x + 2 1/2 = 0. График левой части этого уравнения изображен кривой 3-й, на черт.4. На нем мы видим, что парабола пересекается с осью x-ов в двух точках, абсциссы которых —1 и — 5. Это и будут корни уравнения. Это можно проверить, решив уравнение посредством общей формулы. 2) 1/2 х2 — 2x + 2 = 0 . Составив таблицу частных значений трехчлена
мы построим параболу (черт. 5).
Черт.5 Эта парабола не пересекается с осью x-ов, а только ее касается в точке с абсциссой 2, Уравнение в этом случае имеет только один корень 2. 3) х2 — x + 2 = 0
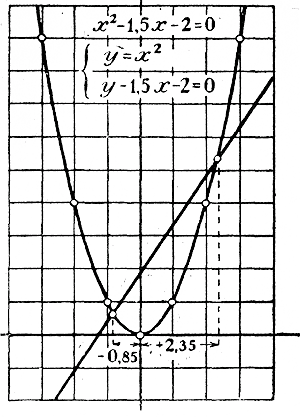
Черт.6 Парабола (черт. 6) не пересекается и не касается оси х-ов; уравнение не имеет вещественных корней. Укажем еще другой прием, более удобный для выполнения. Пусть требуется решить уравнение: х2 — 1,5 x — 2 = 0 , которое можно изобразить так: х2 = 1,5 x + 2 Каждая часть этого уравнения, рассматриваемая отдельно, есть некоторая функция от х. Обозначим функцию, выражаемую левою частью уравнения, буквою y1 и функцию, выражаемую правой частью, буквой y2: y1 = х2 ; y2 = 1,5 x + 2 . Первая функция на чертеже выражается параболой, вторая— прямой линией. Построив на одном и том же чертеже параболу и прямую по их частным значениям:
Черт.7 мы найдем (черт. 7), что прямая и парабола пересекаются в двух точках, абсциссы которых приблизительно выражаются числами 2,35 и—0,85. Это и будут приближенные значения корней данного уравнения, так как при каждой из этих абсцисс ординаты y1 , y2 равны между собой, и следовательно: х2 = 1,5 x + 2 Если случится, что прямая с параболой не пересекается, то уравнение не имеет вещественных корней; если же прямая коснется параболы, то уравнение имеет один корень, равный абсциссе точки касания. Замечание. Так как вычерчивание параболы очень часто требуется для графического решения квадратных уравнений, то для сокращения чертежной работы лучше всего заранее начертить возможно точнее параболу на картоне и из него вырезать параболическое лекало, которым можно пользоваться во многих случаях. На таком лекале надо надписать, какая единица длины была взята при вычерчивании параболы (напр, „за единицу принят 1 см"). 227. Наибольшее и наименьшее значение трехчлена. Когда ветви параболы, изображающей трехчлен у = ax2 + bx + c, направлены вверх (а > 0), тогда из всех ординат есть одна наименьшая; наибольшей ординаты в этом случае нет. Наоборот, когда ветви направлены вниз (а < 0), тогда из всех ординат есть одна наибольшая; наименьшей ординаты в этом случае нет. Значит, трехчлен у = ax2 + bx + c при а > 0 имеет наименьшее значение, не имея наибольшего; при а < 0 имеет наибольшее значение, не имея наименьшего. Чтобы найти величину наибольшего или наименьшего значений, преобразуем трехчлен так, как мы это делали раньше (§ 224).
В таком виде трехчлен представляет собой алгебраическую сумму двух слагаемых: переменного слагаемого Если а > 0, то первое слагаемое при х = — b/2a равно нулю, а при всех прочих значениях х оно есть число положительное, значит, при х = — b/2a трехчлен имеет наименьшее значение, именно Если же a < 0, то первое слагаемое при х = — b/2a попрежиему равно нулю, а при всех прочих значениях х оно есть число отрицательное; следовательно, трехчлен при х = — b/2a получает теперь наибольшее
значение, именно 2281 Изменение трехчлена при изменении х. Изобразив данный трехчлен графически, мы тем самым наглядно представим процесс его изменения при изменении числа х. Возьмем, напр., черт. 4, изображающий трехчлен 1/2 х2 + 3x + 2 1/2 .
Из него видно, что когда х возрастает от — ∞ до — 3, трехчлен убывает от + ∞ до наименьшего значения — 2, переходя при этом через нулевое значение при х = — 5. При дальнейшем возрастании х от — 3 до + ∞ трехчлен возрастает от — 2 до + ∞, переходя при этом через нуль при х = —1. Из чертежа видно также, что 1/2 х2 +
3x + 2 1/2 > 0 при всех
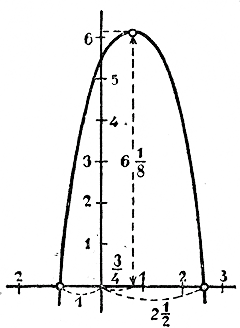
значениях х, меньших —5, и при всех значениях x, больших — 1; Впрочем, чтобы наглядно представить себе процесс изменения данного трехчлена, нет надобности составлять таблицу его частных значений и по ней подробно строить график трехчлена. Пусть, напр., надо проследить изменение трехчлена: y = — 2 х2 + 3x + 5 Для этого можно поступить так: обращая внимание на коэффициент при х2, видим, что он отрицательный. Из этого заключаем, что ветви параболы должны быть направлены вниз, и потому трехчлен имеет наибольшее значение, не имея наименьшего. Найдем корни трехчлена, для чего надо решить уравнение:
Трехчлен имеет два корня, и потому парабола, изображающая его, должна пересекаться два раза с осью х-ов. Найдем еще величину наибольшего значения трехчлена. Для этого преобразуем его так, как мы раньше (§ 224) преобразовывали трехчлен 1/2 х2 + 3x + 2 1/2, а именно так:
Так как произведение — 2( х — 3/4 )2 при х = 3/4 равно 0, а при всех прочих значениях х оно есть число отрицательное, то при х = 3/4 значение трехчлена равно 49/8, а при всех других значениях оно будет меньше этой дроби. Значит, 49/8= 6 1/8 есть наибольшее значение данного трехчлена (при х = 3/4). Таким образом, график трехчлена изобразится так, как на черт.8.
Черт.8 Хотя этот чертеж и приблизительный, тем не менее он наглядно изображает процесс изменения данного трехчлена, а именно, из чертежа видно, что при: возрастании х от — ∞ до —1 трехчлен возрастает от — ∞ до 0; затем при возрастании х от —1 до 3/4 трехчлен продолжает возрастать до 6 1/8 , а при дальнейшем возрастании х от 3/4 до + ∞ трехчлен убывает, переходя во второй раз через нуль при х = 2 1/2 2282. Решение неравенства второй степени с одним неизвестным. Общий вид такого неравенства, по упрощении его, есть следующий: ax2 + bx + c >< 0 Так как знак < всегда может быть приведен к знаку > (умножением обеих частей неравенства на —1), то достаточно рассмотреть неравенства вида: ax2 + bx + c > 0, в котором число а может быть и положительным и отрицательным. Решение этого неравенства основано на свойстве трехчлена ax2 + bx + c разлагаться на множителей первой степени относительно х (§ 221). Обозначив буквами α и β корни этого трехчлена, мы можем заменить его произведением а (х — α)(х — β), и тогда неравенство можно написать так: а (х — α)(х — β) > 0. Рассмотрим отдельно три следующих случая: I. Корни вещественные неравные (что бывает тогда, когда b2 — 4ac > 0, §216). Пусть α > β. Если а > 0, то произведение а (х — α)(х — β), очевидно, тогда положительно, когда каждая из разностей х — α и х — β положительна или каждая отрицательна. Для этого достаточно, чтобы х было больше α (тогда подавно х больше β), или же чтобы х было меньше β (тогда подавно х меньше α). Следовательно, в этом случае неравенство получает решение при х > α и также при х < β, т. е. х должно быть или больше большего корня или меньше меньшего корня. Если же а < 0, то произведение а (х — α)(х — β) тогда положительно, когда одна из разностей х — α и х — β отрицательна, а другая положительна. Для этого достаточно, чтобы х удовлетворяло неравенствам β < х < α, т.е. чтобы х заключалось между корнями трехчлена. II. Корни вещественные равные (что бывает тогда, когда b2 — 4ac = 0). Если α = β, то неравенство «принимает вид: а (х — α)2>0. Так как при всяком вещественном значении х не равном α, число (х — α)2 положительно, то при a > 0 неравенство удовлетворяется всевозможными вещественными значениями х, за исключением х = α, а при a < 0 это неравенство невозможно. III. Корни мнимые (что бывает тогда, когда b2 — 4ac < 0). Пусть α = m + √— n ; в таком случае β = m — √— n Тогда х — α = x — (m + √— n) = (x — m) — √— n х — β = x — (m — √— n ) = (x — m) + √— n . Следовательно, а (х — α)(х — β) = а [(x — m)2 — (√— n)2] = а [(x — m)2 + n] и неравенство можно написать так: а [(x — m)2 + n] > 0. Так как сумма (x — m)2 + n при всяком вещественном значении х есть число положительное, то при а > 0 неравенство удовлетворяется всевозможными значениями x, а при a < 0 оно невозможно. Примеры. 1) Решить неравенство: х2 + 3х — 28 > 0. Корни трехчлена: α = 4, β = — 7. Следовательно, неравенство можно написать так: (х — 4)[х— (—7)] > 0. Отсюда видно, что х > 4 или x < — 7. 2) Решить неравенство: — 4х2 + 28х — 49 > 0 Корни суть: α = β = 3 1/2 Поэтому — 4 (x — 3 1/2)2 > 0, откуда видно, что неравенство невозможно. 3) Решить неравенство: х2 — 4х + 7 > 0. Корни суть: α = 2 + √— 3; β = 2 — √— 3 поэтому неравенство можно написать так: Биквадратное уравнение и некоторые другие. 229. Биквадратное уравнение. Уравнение 4-й степени, напр. такое: х4 — 13х2 + 36 = 0, в которое входят только четные степени неизвестного, называется биквадратным. Оно приводится к квадратному, если заменим х2 через у и, следовательно, х4 через y2 тогда уравнение обратится в квадратное: y2 — 13y + 36 = 0, Решим его:
Но из равенства х2 = у видно, что х = ±√ y . Подставляя сюда на место у найденные числа 9 и 4, получим следующие четыре решения данного уравнения:
Составим формулы для общего вида биквадратного уравнения: aх4 + bх2 + c = 0 Положив х2 = у, получим уравнение ay2 + by + c = 0, из которого находим:
Но так как х = ±√ y то для биквадратного уравнения мы получим следующие 4 решения:
Отсюда видно, что если b2 — 4ас < 0, то все 4 корня мнимые; если же b2 — 4ас >0, то могут быть 3 случая: 1) все корни вещественные (как в приведенном выше численном примере), если 2) все корни мнимые, если оба эти выражения дадут отрицательные числа, и 3) два корня вещественные и два мнимые, если — b +√b2 — 4ас > 0, a Наконец, если b2 — 4ас = 0, то 4 корня делаются попарно равными. 230. Уравнения, у которых левая часть разлагается на множители, а правая есть нуль. Решение таких уравнений сводится к решению уравнений более низких степеней. Так, мы видели (§ 210, II), что для решения неполного квадратного уравнения вида ax2 + bx = 0 надо его левую часть разложить на 2 множителя: х (ах + b) = 0 и затем, приняв во внимание, что произведение равно нулю только тогда, когда какой-нибудь сомножитель равен нулю, свести решение этого уравнения к решению двух уравнений 1-й степени: х= 0 и ах + b = 0. Подобно этому можно решить неполное кубичное уравнение, не содержащее свободного члена, напр, такое: x3 + 3x2 — 10x = 0. Вынеся х за скобки, мы представим уравнение так: х (x2 + 3x — 10) = 0, и, следовательно, оно распадается на 2 уравнения: х = 0 и x2 + 3x — 10 = 0, из которых находим три решения:
Пусть еще уравнение приведено к такому виду: х (х + 4) (x2 — 5x + 6) = 0. Тогда оно распадается на три уравнения: х = 0; х + 4 = 0; x2 — 5x + 6 = 0. Уравнения эти дают: x1 = 0; x2 = — 4; x3 = 2; x4=3. Иррациональные уравнения. 231. Задача. Периметр прямоугольного треугольника равен 10 м, а один из его катетов составляет 2 м; найти две другие стороны этого треугольника. Обозначив другой катет буквою х, найдем, что гипотенуза должна равняться√22 + x2и, следовательно, будем иметь уравнение: 2 + x +√4 + x2 = 10. Мы получили уравнение, в котором неизвестное входит под знак радикала. Уравнения такого рода называются иррациональными. Чтобы решить иррациональное уравнение, его надо предварительно освободить от радикалов, подкоренные выражения которых содержат неизвестное. Если в уравнение, как в нашей задаче, входит только один радикал, то освободиться от него можно таким образом: прежде всего уединим радикал, т. е. перенесем все члены, не содержащие радикала, в одну часть уравнения, оставив радикал в другой части. Тогда наше уравнение будет: √4 + x2 = 10 — 2 — х = 8 — х. Теперь возвысим обе части уравнения в квадрат. Очевидно, что если равные числа мы возвысим в одну и ту же степень, то и получим равные числа; поэтому после возвышения в квадрат знак = сохранится: 4 + x2 = (8 — х)2 ; 4 + x2 = 64 — 16х + x2 Решив это уравнение, найдем: 16х = 64 — 4 = 60; x = 60/16 = 15/4 =3 3/4 Тогда гипотенуза будет:
Пусть еще требуется решить уравнение: 10 —3√3x+21 = 7 Уединим радикал и возвысим в куб: 3 = 3√3x+21 ; 27 = 3x+21; х = 2. Поверка: 10 —3√ 3•2 + 21 = 10 — 3√ 27 = 10 — 3 = 7. 232. Посторонние решения. Возьмем еще такой пример: х = √ x + 7 — 1 (1) Решаем это уравнение так же, как и предыдущее: х + 1 = √ x + 7 ; (2) x2 + 2х + 1 = х +7; (3) x2 + х — 6 = 0 (4)
Подcтавляя найденные решения в уравнения (4), (3), (2) и (1), находим, что оба решения удовлетворяют уравнениям (4) и (3), но уравнениям (2) и (1) удовлетворяет только число 2, а число — 3 не удовлетворяет; это решение является посторонним для уравнений (1) и (2). Значит, оно появилось при переходе от уравнения (2) к уравнению (3), т. е. оно появилось от возвышения частей уравнения (2) в квадрат. Рассмотрим поэтому подробнее, что происходит при возвышении частей уравнения в квадрат. 233. Возвышение частей уравнения в квадрат может ввести посторонние решения. Пусть нам даны два уравнения: х + 1 = √ x + 7 . (1) х + 1 = — √ x + 7 (2) Одно из этих уравнений есть то, которое в предыдущем параграфе нам пришлось возвысить в квадрат, а другое отличается от него только знаком перед радикалом. Возвысив в квадрат обе части каждого из этих двух уравнений, мы получим одно и то же уравнение: x2 + 2х + 1 = х +7 (3) так как (— √ x + 7 )2 и ( √ x + 7 )2 равны одному и тому же числу х + 7. Значит, решения уравнений (1) и (2) должны удовлетворять уравнению (3). Следовательно, уравнение (3) равносильно совокупности уравнений (1) и (2). Поэтому неудивительно, что в числе решений уравнения (3) есть одно, удовлетворящее уравнению (1), и есть другое, удовлетворяющее уравнению (2). Действительно, число — 3 удовлетворяет уравнению (2): — 3 + 1 = — √—3 + 7, т. е. —2 = — 2. Может случиться, что уравнение (2) совсем не имеет решений; тогда решения уравнения (3) будут только те, которые удовлетворяют уравнению (1); значит, тогда посторонних решений не будет вовсе. Может случиться, что данное уравнение (1) не имеет совсем решений; тогда уравнение (3) содержит только решения уравнения (2), и, значит, все они будут посторонние для уравнения (1). Таким образом, возвышение частей уравнения в квадрат может привести к новому уравнению, не равносильному с тем, которое возвышалось.То же самое может случиться и при возвышении частей уравнения в какую-нибудь иную степень. Поэтому, решив уравнение, полученное после возвышения в степень, надо полученные корни испытать подстановкою, с целью определить, нет ли между ними посторонних. 234. Освобождение уравнения от двух квадратных радикалов. Пусть надо решить уравнение с двумя квадратными радикалами, подкоренные выражения которых содержат неизвестное: √2х — 4 — √х + 5 = 1. (1) Желая сначала освободиться от радикала √2х — 4 , предварительно уединим его: √2х — 4 = 1 + √х + 5 . (2) Теперь возвысим это уравнение в квадрат: 2х — 4 = 1 + 2 √х + 5 + х + 5 = 6 + 2 √х + 5 + х, или x —10 = 2√х + 5 . (3) Уравнение это могло также получиться от возвышения в квадрат другого уравнения: —√2х — 4 = 1 + √х + 5 . (4) Следовательно, уравнение (3) включает в себе решения двух уравнений: (2) и (4), и, следовательно, (1) и (4), так как уравнение (2) вполне равносильно уравнению (1). Теперь освободим уравнение (3) от радикала посредством вторичного возвышения в квадрат: x2 — 20x + 100 = 4x + 20, или x2 — 24x + 80 = 0. (5) Уравнение это могло получиться от возвышения в квадрат еще и такого уравнения: x —10 = —2√ х + 5 . (6) Следовательно, оно включает в себе решения уравнений (3) и (6). Но так как уравнение (3) само включает в себе решения уравнений (1) и (4), то, значит, уравнение (5) включает в себе решения 3 уравнений: (1), (4) и (6). Решим теперь уравнение (5): x = 12 ± √144 — 80 = 12 ± √64 = 12 ± 8; x1=12 + 8 = 20; x2 = 12 — 8 = 4. Подстановкою убеждаемся, что данное уравнение (1) удовлетворяется только числом 20, а число 4 ему не удовлетворяет. Это число удовлетворяет уравнению (6). Замечания. 1) Предложенное уравнение можно решить, и не уединяя радикала. Возвысив в квадрат обе части уравнения (1), мы получим уравнение только с одним радикалом: 2х — 4 —2√(2х — 4)(х + 5 ) + х +5 = 1. От этого радикала освободимся, как обыкновенно (уединив его): 3х = 2√(2х — 4)(х + 5 ) ; 9x2 = 4 (2х — 4) (х + 5); 9x2 — 8x2 + 16х — 40х + 80 = 0; x2 — 24x + 80 = 0. 2) Существуют способы освобождения уравнения от какого угодно числа радикалов и не только квадратных, но и других степеней. Мы ограничились указанием лишь самых простых случаев, чаще всего встречающихся. Системы уравнений второй степени. 235. Степень уравнения с несколькими неизвестными. Чтобы определить степень уравнения, в которое входят несколько неизвестных, надо предварительно это уравнение упростить (раскрыть скобки, освободиться от радикалов и знаменателей, которые содержат неизвестные, и сделать приведение подобных членов). Тогда степенью уравнения называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая. Напр., 3
уравнения: х2 + 2ху — х + 2 = 0, Мы рассмотрим сейчас, как решаются некоторые простейшие системы уравнений 2-й степени с 2 неизвестными. 236. Система двух уравнений, из которых одно первой степени, а другое второй. Пусть дана система:
Всего удобнее такую систему решить способом подстановки следующим путем (см. отдел 5 глава 1§ 141). Из уравнения 1-й степени определяем одно какое-нибудь неизвестное, как функцию от другого неизвестного, напр., определяем у, как функцию от х: у = 2х — 1. Тогда уравнение 2-й степени после подстановки дает уравнение с одним неизвестным х:
После этого из уравнения у = 2х — 1 находим: y1 = 2 • 1 — 1 = 1 y2 = 2 • 8/15 — 1 = 1/15 Таким образом, данная система имеет две пары решений: 1) x1 = l , y1 = 1; 2) х2 = 8/15 , y2 = 1/15 Подобным путем всегда можно решить систему двух уравнений, если одно уравнение первой степени, а другое — второй. Так, напр., легко решается система: х + у = а , ху = b. Впрочем, эту систему можно решить весьма просто иначе. Так как уравнения дают сумму и произведение неизвестных, то эти неизвестные можно рассматривать как корни такого приведенного квадратного уравнения, у которого коэффициент при х равен — а, а свободный член есть b: z2— az + b = 0. Один корень этого уравнения можно принять за х, а другой за у. Значит:
237. Система двух уравнений, из которых каждое второй степени. Такая система вообще не решается элементарно, так как ее решение сводится к решению полного уравнения 4-й степени, а такие уравнения в элементарной алгебре не рассматриваются. Но в некоторых частных случаях можно указать элементарное решение. Пример. x2 + y2 = а , ху = b. Если b =/= 0, то и х =/= 0 и у =/= 0 4). Поэтому мы можем, не нарушая равносильности уравнений, разделить обе части второго из них на х: у = b/x Тогда первое уравнение дает: x2 + ( b/x )2 = a Умножив обе части на x2, получим равносильное уравнение: x4 + b2 = ax2 , т. е. x4 — ax2 + b2 = 0. Решив это биквадратное уравнение, найдем для х четыре значения. Вставив каждое из них в формулу, выведенную для у, найдем четыре соответствующих значения для у. Подобным же образом решается и система: x2 — y2 = а, xy = b. 238. Графический способ решения. Начертив графики каждого из данных уравнений (при помощи таблиц частных значений х и у), находим величины координат точек пересечения этих графиков; это и будут корни уравнений. Пример. Решить систему: 1) у = x2 — bх + 2, 2) х = 2y2 — 3. Составим таблицу частных значений х и у для уравнения 1-го:
и таблицу частных значений для уравнения 2-го:
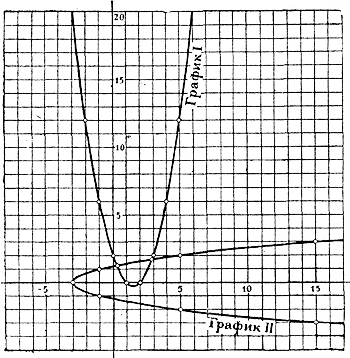
По этим значениям построим графики (эти графики будут параболы, черт.9):
Черт.9 Графики пересекаются в двух точках, координаты которых приблизительно будут: х = 0,3; у = 1,3 и х = 2,8; у = 1,6. Можно найти координаты точек пересечения точнее, если начертим в более широком масштабе те части графиков, которые лежат около точек пересечения. Заметив, что абсциссы точек пересечения лежат: одна между 0 и 1, другая между 2 и 3 и что ординаты их заключены между 1 и 2, составим такие таблицы: Для уравнения 1-го
Для уравнения 2-го
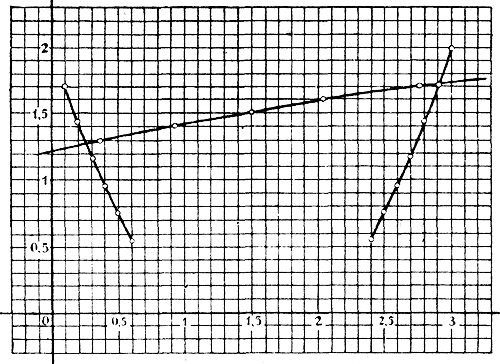
Теперь нанесем эти значения на черт. 10:
Из такого чертежа координаты точек пересечения, конечно, могут быть определены точнее (х = 0,26, у = 1,28; х = 2,91, у =1,71).
|